国会ダイジェスト字幕付き】児玉龍彦教授、渾身の訴え「このままでは来月は目を覆うような惨状になる・・・」コロナ対策とGoToについて言及【参議院新型コロナ閉会中審査】
1:15~ 現在の日本の現状
6:54~ 検査数増加に伴う陽性率増加について
14:56~ GoToキャンペーンについて
@YouTube c=42817
d=41860
e=361
f1=18321
fmax=1e6
f=0
flg=F
while(!flg | f<fmax){
f=f+1
flg <- (f*e)%%d==1
if(flg & f<fmax) print(f)
}
> c=42817
> d=41860
> e=361
> f1=18321
> fmax=1e6
> f=0
> flg=F
> e
[1] 361
> re=NULL
> while(!flg | f<fmax){
+ f=f+1
+ flg <- (f*e)%%d==1
+ if(flg & f<fmax) re=c(re,f)
+ }
> re
[1] 18321 60181 102041 143901 185761 227621 269481 311341 353201 395061
[11] 436921 478781 520641 562501 604361 646221 688081 729941 771801 813661
[21] 855521 897381 939241 981101
>
c=42817
d=41860
e=361
f1=18321
fmax=1e6
f=0
flg=F
e
re=NULL
while(!flg | f<fmax){
f=f+1
flg <- (f*e)%%d==1
if(flg & f<fmax) re=c(re,f)
}
n=as.bigz(3047)
for(f in re){
print( n^f%%c )
}
c=42817
d=41860
e=361
f1=18321
fmax=1e6
f=0
flg=F
re=NULL
while(!flg | f<fmax){
f=f+1
flg <- (f*e)%%d==1
if(flg & f<fmax) re=c(re,f)
}
n=as.bigz(3047)
for(f in re){
print( n^f%%c )
}
>>197 北の方が酷いと思う
そもそも医者が残らないし
旭川と弘前は黒だわ
### 暗号解読 ###
rm(list=ls())
# 公開鍵 (c,e)
c=42817
e=361
# 暗号
n=3047
# 素因数分解してdを決定
library(gmp)
(c1=gmp::factorize(c)) # 計算機にcを素因数分解させて
(d=prod((c1-1))) # 素因数-1の積dを求める
# fを虱潰しに探す
fmax=1e6 # 探索させる秘密鍵 (c,f)のｆの上限=10^6
f=0 # 初期値
flg=FALSE # 条件をみたすか否かのフラッグ
re.f=NULL # fの候補を容れる数列
# fmax以下でf*eをdで割った余りが1となるfの値を数をre.fに追加する
while(!flg | f<=fmax){
f=f+1 # 1増やして
flg <- (f*e)%%d==1 # f*e (mod d)が1に等しいか?
if(flg & f<=fmax) re.f=c(re.f,f) # 等しければre.fに追加
}
re.f # 秘密鍵(c,f)のfの候補
decode=NULL # 秘密鍵(c,f)を使っての復号
for(f in re.f){
decode=append(decode,asNumeric(mod.bigz(pow.bigz(n,f),c)))
}
decode
> # 素因数分解してdを決定
> library(gmp)
> (c1=gmp::factorize(c)) # 計算機にcを素因数分解させて
Big Integer ('bigz') object of length 2:
[1] 47 911
> (d=prod((c1-1))) # 素因数-1の積dを求める
Big Integer ('bigz') :
[1] 41860
>
> # fを虱潰しに探す
> fmax=1e6 # 探索させる秘密鍵 (c,f)のｆの上限=10^6
> f=0 # 初期値
> flg=FALSE # 条件をみたすか否かのフラッグ
> re.f=NULL # fの候補を容れる数列
> # fmax以下でf*eをdで割った余りが1となるfの値を数をre.fに追加する
> while(!flg | f<=fmax){
+ f=f+1 # 1増やして
+ flg <- (f*e)%%d==1 # f*e (mod d)が1に等しいか?
+ if(flg & f<=fmax) re.f=c(re.f,f) # 等しければre.fに追加
+ }
> re.f # 秘密鍵(c,f)のfの候補
[1] 18321 60181 102041 143901 185761 227621 269481 311341 353201 395061 436921
[12] 478781 520641 562501 604361 646221 688081 729941 771801 813661 855521 897381
[23] 939241 981101
> decode=NULL # 秘密鍵(c,f)を使っての復号
> for(f in re.f){
+ decode=append(decode,asNumeric(mod.bigz(pow.bigz(n,f),c)))
+ }
> decode
[1] 123 123 123 123 123 123 123 123 123 123 123 123 123 123 123 123 123 123 123 123
[21] 123 123 123 123
ｒｍ（ｌｉｓｔ＝ｌｓ（））
＃＃ 暗号化 ｂｙ ＲＳＡ ＂ＡＨＯ＂ －＞ ｃｉｐｈｅｒ， ｐｕｂｌｉｃ＿ｋｅｙ， ｓｅｃｒｅｔ＿ｋｅｙ
Ｅｎｃｏｄｅ ＜－ ｆｕｎｃｔｉｏｎ（ｘ＝＂ＡＨＯ＂，ｋ＝１ｅ４）｛ ＃ 設定素数の上限
＃＃ －－ 文字列を数値化 －－
＃ ｃｈａｒａｃｔｏｒ ｔｏ ｎｕｍｂｅｒ
ｃ２ｎ ＜－ ｆｕｎｃｔｉｏｎ（ｃ）｛ ＃ ＇Ａ＇ －＞ １１，＇Ｂ＇－＞１２，．．．，＇Ｚ＇－＞３７，＇０＇－＞７０， ＇１＇－＞ ７１
ｓｙｍｂｏ＝ｃ（＇ ＇，＇＿＇，＇！＇，＇＋＇，＇－＇，＇＊＇，＇／＇）
ＬＥＴ＝ｃ（ＬＥＴＴＥＲＳ，ｌｅｔｔｅｒｓ，ｓｙｍｂｏ，０：９）
ｘ＝（ＬＥＴ［１：６９］＝＝ｃ）
ｉｆ（ａｎｙ（ｘ）） １０＋ｗｈｉｃｈ（ｘ）
ｅｌｓｅ ０
｝
＃ ｓｔｒｉｎｇ ｔｏ ｄｉｇｉｔｓ
ｓ２ｄ ＜－ ｆｕｎｃｔｉｏｎ（ｓ）｛ ＃ ＂ＯＨ＂ －＞ ２５１８
ｎｃ＝ｎｃｈａｒ（ｓ）
ｄｃ＝ｃｈａｒａｃｔｅｒ（）
ｆｏｒ（ｉ ｉｎ １：ｎｃ）｛
ｘ＝ｃ２ｎ（ｓｕｂｓｔｒ（ｓ，ｉ，ｉ））
ｄｃ［ｉ］＝ｉｆｅｌｓｅ（ｘ！＝０，ａｓ．ｃｈａｒａｃｔｅｒ（ｘ），＂００＂）
｝
ｒｅ＝ｐａｓｔｅ０（ｄｃ，ｃｏｌｌａｐｓｅ＝＇＇）
ｃａｔ（ｓ，＇－＞＇，ｒｅ，＇\ｎ＇）
ｉｎｖｉｓｉｂｌｅ（ａｓ．ｎｕｍｅｒｉｃ（ｒｅ））
｝
＃＃ －－ ＲＳＡ アルゴリズム
ｌｉｂｒａｒｙ（ｎｕｍｂｅｒｓ）
ｌｉｂｒａｒｙ（ｇｍｐ）
ｏｐｔｉｏｎｓ（ｄｉｇｉｔｓ＝２２）
＃ １．素数ａ，ｂを決める（上限＝ｋ）
（ａｂ＝ｓａｍｐｌｅ（Ｐｒｉｍｅｓ（ｋ），２））
ａ＝ａｂ［１］ ； ｂ＝ａｂ［２］
＃ ２．ｃ＝ａｂとおく
（ｃ＝ａ＊ｂ）
＃ ３．ｄ＝（ａ－１）（ｂ－１）とおく
（ｄ＝（ａ－１）＊（ｂ－１））
＃ ４．ｄと互いに素な自然数ｅを一つ決める
ｆｌｇ＝ＦＡＬＳＥ
ｗｈｉｌｅ（！ｆｌｇ）｛
ｅ＝ｓａｍｐｌｅ（ｋ，１）
ｆｌｇ ＜－ ＧＣＤ（ｄ，ｅ）＝＝１
｝
＃ ５．ｆｅをｄで割った余りが１となる自然数ｆを求める
ｆｌｇ＝ＦＡＬＳＥ
ｆ＝０
ｗｈｉｌｅ（！ｆｌｇ）｛ ＃ ｃｏｕｌｄ ｂｅ ｌｅｎｇｔｈｙ ｐｒｏｃｅｓｓ ．．．．
ｆ＝ｆ＋１
ｆｌｇ ＜－ （ｆ＊ｅ）％％ｄ＝＝１
｝
＃ ６．ペア（ｃ，ｅ）を公開鍵、ペア（ｃ，ｆ）を秘密鍵とする
（ｐｕｂｌｉｃ＿ｋｅｙ＝ｃ（ｃ，ｅ））
（ｓｅｃｒｅｔ＿ｋｅｙ＝ｃ（ｃ，ｆ））
＃ ７．平文（を自然数に変換）をｍとすると暗号文はｍ＾ｅをｃで割った余りｎである
ｍ＝ａｓ．ｂｉｇｚ（ｓ２ｄ（ｘ））
ｉｆ（ｍ＜ｃ）｛ ＃ ｍ ＜ ｃ の時のみ暗号化
ｎ＝ｍ＾ｅ％％ｃ
｝ｅｌｓｅ｛
ｎ＝ＮＵＬＬ
｝
ｌｉｓｔ（ｃｉｐｈｅｒ＝ｎ，ｐｕｂｌｉｃ＿ｋｅｙ＝ｐｕｂｌｉｃ＿ｋｅｙ，ｓｅｃｒｅｔ＿ｋｅｙ＝ｓｅｃｒｅｔ＿ｋｅｙ）
｝
Ｅｎｃｏｄｅ（＂ＡＨＯ＂）
＃＃＃ Ｄｅｃｏｄｅ 復号化 ＃＃＃
Ｄｅｃｏｄｅ ＜－ ｆｕｎｃｔｉｏｎ（ｃｉｐｈｅｒ，ｓｅｃｒｅｔ＿ｋｅｙ１，ｓｅｃｒｅｔ＿ｋｅｙ２）｛
＃ ｎｕｍｂｅｒ ｔｏ ｃｈａｃｔｅｒ
ｎ２ｃ ＜－ ｆｕｎｃｔｉｏｎ（ｎ）｛ ＃ １１ －＞ ＇Ａ＇， １２ －＞ ＇Ｂ＇，．．．， ７３ －＞ ＇３＇
ｓｙｍｂｏ＝ｃ（＇ ＇，＇＿＇，＇！＇，＇＋＇，＇－＇，＇＊＇，＇／＇）
ＬＥＴ＝ｃ（ＬＥＴＴＥＲＳ，ｌｅｔｔｅｒｓ，ｓｙｍｂｏ，０：９）
ｉｆ（１０＜ｎ ＆ ｎ＜７９）｛
ＬＥＴ［ｎ－１０］
｝ｅｌｓｅ ｒｅｔｕｒｎ（＇？＇） ＃ ９９ －＞ ？
｝
＃ ｄｉｇｉｔｓ ｔｏ ｓｔｒｉｎｇ
ｄ２ｓ ＜－ ｆｕｎｃｔｉｏｎ（ｄ）｛ ＃ １２３４５６ －＞ ＢＸｔ
ｓ＝ａｓ．ｃｈａｒａｃｔｅｒ（ｄ）
ｎｃ＝ｎｃｈａｒ（ｓ）
ｉｆ（ｎｃ％％２＝＝０）｛
ｃｈ＝ｃｈａｒａｃｔｅｒ（）
ｆｏｒ（ｉ ｉｎ １：（ｎｃ％／％２））｛
ｃｈ［ｉ］＝ｎ２ｃ（ａｓ．ｉｎｔｅｇｅｒ（ｓｕｂｓｔｒ（ｓ，２＊ｉ－１，２＊ｉ）））
｝
｝ｅｌｓｅ ｒｅｔｕｒｎ（０）
ｒｅ＝ｐａｓｔｅ０（ｃｈ，ｃｏｌｌａｐｓｅ＝＇＇）
ｃａｔ（ｒｅ，＇\ｎ＇）
ｉｎｖｉｓｉｂｌｅ（ｒｅ）
｝
ｌｉｂｒａｒｙ（ｇｍｐ）
ｍ＝ｍｏｄ．ｂｉｇｚ（ｐｏｗ．ｂｉｇｚ（ｃｉｐｈｅｒ，ｓｅｃｒｅｔ＿ｋｅｙ２），ｓｅｃｒｅｔ＿ｋｅｙ１）
ｄ２ｓ（ａｓＮｕｍｅｒｉｃ（ｍ））
｝
Ｅｎｃｏｄｅ（＂ＢＡＫＡ＂）
Ｄｅｃｏｄｅ（９９０５３８４，９０８７６９１１，７７９５７４０７）
10Lの容器いっぱいに油が入っています。7Lの容器と3Lの容器を使って、この油を5Lずつに分けます。どのような分け方がありますか。
move7 <- function(xy){
x=xy[1] ; y=xy[2]
# x==7
if(x==7) re=c(7-(3-y),3)
# x==0
if(x==0) re=c(7,y)
# y==3
if(y==3) re=c(x,0)
# y==0
if(y==0 & x!=7){
if(x>=3) re=c(x-3,3)
else re=c(0,x)
}
if(0<=re[1] & re[1]<=7 & 0<=re[2] & re[2]<=3) return(re)
else return(FALSE)
}
move7(c(7,0))
move7(move7(c(7,0)))
move7(move7(move7(c(7,0))))
move7(move7(move7(move7(c(7,0)))))
move7(move7(move7(move7(move7(c(7,0))))))
move7(move7(move7(move7(move7(move7(c(7,0)))))))
move7(move7(move7(move7(move7(move7(move7(c(7,0))))))))
move7(move7(move7(move7(move7(move7(move7(move7(c(7,0)))))))))
status=c(7,0)
cat('1 : ',status,'\n')
i=1
while(!identical(status,c(0,0))){
i=i+1
status=move7(status)
cat(i,' : ',status,'\n')
}
> status=c(7,0)
> cat('1 : ',status,'\n')
1 : 7 0
> i=1
> while(!identical(status,c(0,0))){
+ i=i+1
+ status=move7(status)
+ cat(i,' : ',status,'\n')
+ }
2 : 4 3
3 : 4 0
4 : 1 3
5 : 1 0
6 : 0 1
7 : 7 1
8 : 5 3
9 : 5 0
10 : 2 3
11 : 2 0
12 : 0 2
13 : 7 2
14 : 6 3
15 : 6 0
16 : 3 3
17 : 3 0
18 : 0 3
19 : 0 0
move3 <- function(xy){ # start from c(0,3)
x=xy[1] ; y=xy[2]
if(y==3){
if(x<=(7-3)) re=c(x+3,0)
else re=c(7, 3-(7-x))
}
if(y==0) re=c(x,3)
if(x==7) re=c(0,y)
if(x==0) re=c(y,0)
return(re)
}
status=c(0,3)
cat('1 : ',status,'\n')
i=1
while(!identical(status,c(0,0))){ # stop at c(5,0) for solution
i=i+1
status=move3(status)
cat(i,' : ',status,'\n')
}
> cat('1 : ',status,'\n')
1 : 0 3
> while(!identical(status,c(0,0))){ # stop at c(5,0) for solution
+ i=i+1
+ status=move3(status)
+ cat(i,' : ',status,'\n')
+ }
2 : 3 0
3 : 3 3
4 : 6 0
5 : 6 3
6 : 7 2
7 : 0 2
8 : 2 0
9 : 2 3
10 : 5 0
11 : 5 3
12 : 7 1
13 : 0 1
14 : 1 0
15 : 1 3
16 : 4 0
17 : 4 3
18 : 7 0
19 : 0 0
７リットルから開始で９回の移動、３リットルから開始で１０回の移動で５リットルが測れる
>>190 ９から始めた方がステップがすくないな
> a7=9 ; b3=7
1 : 9 0
2 : 2 7
3 : 2 0
4 : 0 2
5 : 9 2
6 : 4 7
7 : 4 0
8 : 0 4
9 : 9 4
10 : 6 7
11 : 6 0
12 : 0 6
13 : 9 6
14 : 8 7
15 : 8 0
6を法として+1に合同な素数と、-1に合同な素数が、p以下に同数あるような素数pを「均衡素数」と呼ぶことにする。
(例えば2,3,7,13は均衡素数だが、5,11はそうでない)
このとき、 均衡素数を20個見つけよ
F <- function(N){
library(numbers)
prime=Primes(N)
n_p=length(prime)
f1 <- function(x) x%%6==1
f5 <- function(x) x%%6==5
p1=prime[sapply(prime,f1)]
p5=prime[sapply(prime,f5)]
f <- function(p) sum(p1<=p)==sum(p5<=p)
p=NULL
i=1
lp=length(p)
while(i <= n_p){
x=prime[i]
if(f(x)==TRUE) p=c(p,x)
lp=length(p)
i=i+1
}
p
}
F(1e3)
F(1e4)
F(1e5)
F(1e6)
"
容量8Lの袋と容量5Lの袋を使って池の水を丁度4L集めたい。
袋に目盛りはついていません。
袋から袋への移し替えは全量で行います。
池からとる水の量や池に捨てる水の量には制限はありません。
最初に片方に満たした作業を１回目として
丁度4Lを集めるのに最低何回の移動が必要か？
"
a7=8 ; b3=5
# starting from the bigger pitcher
movea7 <- function(xy){ # start from c(a7,0)
x=xy[1] ; y=xy[2]
# x==a7
if(x==a7) re=c(a7-(b3-y),b3)
# x==0
if(x==0) re=c(a7,y)
# y==b3
if(y==b3) re=c(x,0)
# y==0
if(y==0 & x!=a7){
if(x>=b3) re=c(x-b3,b3)
else re=c(0,x)
}
return(re)
}
STATUS=status=c(a7,0)
i=1
while(!identical(status,c(0,0))){#
i=i+1
status=movea7(status)
STATUS=rbind(STATUS,status)
}
rownames(STATUS)=1:nrow(STATUS)
colnames(STATUS)=c(paste0(a7,'L'),paste0(b3,'L'))
STATUS
# starting from the smaller pitcher
moveb3 <- function(xy){ # start from c(0,b3)
x=xy[1] ; y=xy[2]
if(y==b3){
if(x<=(a7-b3)) re=c(x+b3,0)
else re=c(a7, b3-(a7-x))
}
if(y==0) re=c(x,b3)
if(x==a7) re=c(0,y)
if(x==0) re=c(y,0)
return(re)
}
STATUS=status=c(0,b3)
i=1
while(!identical(status,c(0,0))){ # stop at c(5,0) for solution
i=i+1
status=moveb3(status)
STATUS=rbind(STATUS,status)
}
rownames(STATUS)=1:nrow(STATUS)
colnames(STATUS)=c(paste0(a7,'L'),paste0(b3,'L'))
STATUS
> STATUS
8L 5L
1 0 5
2 5 0
3 5 5
4 8 2
5 0 2
6 2 0
7 2 5
8 7 0
9 7 5
10 8 4
11 0 4
12 4 0
13 4 5
14 8 1
15 0 1
16 1 0
17 1 5
18 6 0
19 6 5
20 8 3
21 0 3
22 3 0
23 3 5
24 8 0
25 0 0
> STATUS
8L 5L
1 8 0
2 3 5
3 3 0
4 0 3
5 8 3
6 6 5
7 6 0
8 1 5
9 1 0
10 0 1
11 8 1
12 4 5
13 4 0
14 0 4
15 8 4
16 7 5
17 7 0
18 2 5
19 2 0
20 0 2
21 8 2
22 5 5
23 5 0
24 0 5
25 0 0
SEIRモデルにK値という指標を重ねてこんなグラフを作って遊んでみた。
K値の評価を検査していたら
https://tatsuharug.com/kvalue ページにあたった。
獣医にも賢い人がいるなぁ、と思って経歴をみたら、
https://tatsuharug.com/profile#i-5 納得した。
abc2ABC <- function(a,b,c,axis=FALSE,...){ # 三辺の長さを与えて角度を計算して三角形を描画する
abc=c(a,b,c)
if((0<a & 0<b & 0<c) & ( max(abc) < sum(abc[-which.max(abc)]))){
A=acos((b^2+c^2-a^2)/(2*b*c))
B=acos((c^2+a^2-b^2)/(2*c*a))
C=acos((a^2+b^2-c^2)/(2*a*b))
ABC=c(A,B,C)
plot(NULL,asp=1,xlim=c(0,max(abc)),ylim=c(0,max(abc)),bty='n',
ann=F,axes=axis)
segments(0,0,c,0,...)
segments(0,0,b*cos(A),b*sin(A),...)
segments(c,0,b*cos(A),b*sin(A),...)
return(list(ABCrad=ABC,ABCdeg=ABC*180/pi))
}else return(0)
}
abc2ABC(12,13,5,col=2)
abc2ABC(3,3,3,T,col=2)
# 放物線y=x^2 0<=x<=1の回転体の容器に水を入れて45度傾ける
par(bty='l')
source('tools.R')
x=seq(-1,1,0.01)
curve(x^2,-1,1,asp=1,ann=F)
x=seq(0,1,0.01)
segments(x,x^2,x,x,col='blue')
integrate(function(z) pi*sqrt(z)^2, 0,1)
seg(0+0i,0+0.6i,col=8) ; pt(0+0.3i,'z')
seg(0+0.6i,sqrt(0.6)+0.6i,col=8) ; pt(0.3+0.6i,'√z')
integrate(function(y) pi*sqrt(y)^2, 0,1)$value ; pi/2
integrate(function(x)x-x^2,0,1)$value ; 1/6
# x^2+y^2=z
x=y=seq(-1,1,0.1)
f <- function(x,y) x^2+y^2
z=outer(x,y,f)
rgl::persp3d(x,y,z,zlim=c(0,1),asp=1,col=rgb(0.99,0.99,0.99,0.99))
z[z>1]=1
persp(x,y,z, theta=35, lty=3,col='lightgreen',xlab='x',ylab='y',zlab='z',
ticktype='detailed',shade=0.4,phi=30,ltheta=-10,border=TRUE)
>>231 x＝x^2+t^2
α=1/2 (1 - sqrt(1 - 4 t^2))
β=1/2 (1 + sqrt(1 - 4 t^2))
t=[-1/2,1/2]
β-α=2*sqrt(1-4*t^2)
f=function(x) (2*sqrt(1-4*x^2))^3/6
integrate(f, -1/2,1/2)
x＝x^2+t^2
α=1/2 (1 - sqrt(1 - 4 t^2))
β=1/2 (1 + sqrt(1 - 4 t^2))
t=[-1/2,1/2]
β-α=sqrt(1-4*t^2)
f=function(x) (sqrt(1-4*x^2))^3/6
integrate(f, -1/2,1/2)$value/pi
x＝x^2+t^2
α=1/2 (1 - sqrt(1 - 4 t^2))
β=1/2 (1 + sqrt(1 - 4 t^2))
t=[-1/2,1/2]
β-α=sqrt(1-4*t^2)
f=function(x) (sqrt(1-4*x^2))^3/6
integrate(f, -1/2,1/2)$value
k*x＝a*x^2+t^2
α=1/2 (1 - sqrt(1 - 4 t^2))
β=1/2 (1 + sqrt(1 - 4 t^2))
t=[-1/2,1/2]
β-α=sqrt(1-4*t^2)
f=function(x) (sqrt(1-4*x^2))^3/6
integrate(f, -1/2,1/2)$value/pi
(β-α)^2=(α+β)^2-4αβ=(k/a)^2-4t^2/a
# y=ax^2の放物線回転体で上縁の半径がrである器をdeg度傾けて残る液体の量
Tilt <- function(deg=45,a=1,r=1){
θ=deg*pi/180
max=atan(2*a*r)
if(θ>max) return(0)
f <- function(x){
(a/6)* ((1/a)*sqrt(4*a^2*r^2 - 4*a^2*x^2 - 4*a*r*tan(θ) + tan(θ)^2))^3
}
abs(integrate(f,-(tan(θ)/(2*a)-r),tan(θ)/(2*a)-r)$value)
}
degs=seq(0,atan(2)*180/pi,length=500)
Volume=sapply(degs,Tilt)
plot(degs,Volume,xlab='傾き',ylab='残像量',type='l',lwd=2)
# 残りの液量割合から傾ける角度を算出
uniroot(function(x) Tilt(x)-Tilt(0)/2, c(0,60))$root
Vol2deg <- function(vol=0.5,A=1,R=1){ # proportion of the full-filled volume
uniroot(function(x) Tilt(x,A,R) - vol*Tilt(0,A,R),c(0,atan(2*A*R)*180/pi))$root
}
Vol2deg(0.5)
vol=1:20/20
data.frame(残量割合=vol,傾斜角度=sapply(vol,Vol2deg))
vols=seq(0,1,0.01)
plot(vols,sapply(vols,Vol2deg),type='l',col='navy',lwd=2,
xlab='残存割合',ylab='傾斜角度')
>>231 これ類題が東大入試の過去問にあるんだよなぁ。
俺が受験した頃でも、とても試験時間内に解けるとは思えん。
(draft)
" y=f(x)
y=sqrt(r^2-x^2)
f(sqrt(x^2+y^2))
= sqrt(r^2-x^2-y^2)
"
fc = function(x,r=1) 1-sqrt(r^2-x^2)
fc=Vectorize(fc)
curve(fc(x),asp=1)
f = function(x,y,r=1){
if(r^2-(x^2+y^2) > 0) 1-sqrt(r^2-(x^2+y^2))
else 0
}
f=Vectorize(f)
x=y=seq(-1,1,0.01)
z=outer(x,y,f1)
rgl::persp3d(x,y,z,zlim=c(0,1),col=2)
(draft)
" y=f(x)
y=sqrt(r^2-x^2)
f(sqrt(x^2+y^2))
= sqrt(r^2-x^2-y^2)
"
fc = function(x,r=1) 1-sqrt(r^2-x^2)
fc=Vectorize(fc)
curve(fc(x),asp=1)
f = function(x,y,r=1){
if(r^2-(x^2+y^2) > 0) 1-sqrt(r^2-(x^2+y^2))
else NA
}
f=Vectorize(f)
x=y=seq(-1,1,0.01)
z=outer(x,y,f)
idx=which(z!=NA)
z=z[idx]
x=x[idx]
y=y[idx]
rgl::persp3d(x,y,z,zlim=c(0,1),col=2)
(draft)
" y=f(x)
y=sqrt(r^2-x^2)
f(sqrt(x^2+y^2))
= sqrt(r^2-x^2-y^2)
"
fc = function(x,r=1) 1-sqrt(r^2-x^2)
fc=Vectorize(fc)
curve(fc(x),asp=1)
f = function(x,y,r=1){
if(r^2-(x^2+y^2) > 0) 1-sqrt(r^2-(x^2+y^2))
else NA
}
f=Vectorize(f)
x=y=seq(-1,1,0.01)
z=outer(x,y,f)
idx=which(z!=NA)
z=z[idx]
x=x[idx]
y=y[idx]
rgl::persp3d(x,y,z,zlim=c(0,1),col=2)
http://cse.naro.affrc.go.jp/takezawa/r-tips/r/38.html 関数 polyroot() で多項式の解（根）を求めることが出来る．例えば，p(x) = 5 + 4x + x2 の根を求める場合は c(5, 4, 1) を与える．
"
25枚の山札があり内1枚がレアカードだとします。
25枚の山札から10枚を引いて手札にし、
更に手札の10枚のうち2枚を山札から交換できる場合
（交換は、交換したいカードを山札でない場所に捨てたあとに山札から引きます)
"
# exchange n cards
exch <- function(x,y,n){
nx=length(x)
ny=length(y)
ix=sample(nx,n) # index of x exchanged
iy=sample(ny,n)
X=c(y[iy],x[-ix])
Y=c(x[ix],y[-iy])
list(X,Y)
}
#
sim <- function(
r=1, # レアカードの枚数
n25=25, # 最初の山札の枚数
n10=10, # 最初に引く手札の枚数
e2=2){ # 交換する枚数
t10=sample(n25,n10) # 交換前の手札10枚
y15=(1:n25)[-t10] # 交換前の山札15枚
te=exch(t10,y15,e2)[[2]] # 交換後の手札
any(1:r %in% te) # １枚でもレアカードを含むか？
}
mean(replicate(1e6,sim(1))) # レアカード１枚
mean(replicate(1e6,sim(2))) # レアカード２枚
半球状のお椀をθ傾けたときの残量
y1=r+tanθ(x-r)
y2=r-sqrt(r^2-(x^2+t^2))
α = r sin^2(θ) - cos^2(θ) sqrt(r^2 - t^2 - t^2 tan^2(θ))
β = r sin^2(θ) + cos^2(θ) sqrt(r^2 - t^2 - t^2 tan^2(θ))
y1-y2=tanθ(x-r) + sqrt(r^2-(x^2+t^2))
S(t)=integrate[α,β] (y1-y2)dx
integrate[-rcosθ,rcosθ] S(t)dt
Volume <- function(deg,r=1){
θ=deg*pi/180
g <- function(t){
f <- function(x){
tan(θ)*(x-r) + sqrt(r^2-(x^2+t^2))
}
integrate(f,
r*sin(θ)^2 - cos(θ)^2*sqrt(r^2-t^2-t^2*tan(θ)^2),
r*sin(θ)^2 + cos(θ)^2*sqrt(r^2-t^2-t^2*tan(θ)^2))$value
}
integrate(Vectorize(g),-r*cos(θ),r*cos(θ))$value
}
Volume(0) ; (4/3)*pi/2
degs=0:90
vol=sapply(degs,Volume)/Volume(0)
plot(degs,vol,type='l') ; abline(h=0.5,lty=3)
uniroot(function(x) Volume(x)/Volume(0)-0.5,c(15,30))$root
数値積分して値を出したが
数学板ではあっという間に厳密解を出されてしまった。
数値解と一致していて安心した。
>>
半球面お碗を角度 θ 傾けて 液体を半分にするには...
V(θ) = r^3 ∫[x=sinθ..1] dx π* { √(1-x^2) }^2
= πr^3 ∫[x=sinθ..1] dx ( 1-x^2 ) = r^3 (x - x^3/3 )[x=sinθ, 1]
= πr^3 { 1-sinθ - (1-(sinθ)^3)/3 }
= πr^3 { 2/3 -t + t^3/3 } (t = sinθ と置いた)
V(θ)/V(0) = 3/2 * { 2/3 - t + t^3/3 } = 1/2 よって t^3 - 3t + 1 = 0 を解く。
WolframAlpha で "solve t^3 - 3t + 1 = 0" とやると 第2根が [0,1] の範囲に来るので,
θ = arcsin(t) = arcsin( √(2 - √3 cos(π/18) - sin(π/18)) ) = 20.322... [deg]
と求まる。
どうやら √(2 - √3 cos(π/18) - sin(π/18)) = 2cos4π/9 が成り立つらしい。
3次方程式: x^3 - αx + β = 0 の解について
3倍角公式: 4cos³θ -3cosθ - cos(3θ) = 0
を 4c³ -3c - C = 0 と書く
0 = a³/4*(4c³ -3c - C) = (ac)³ - (3a²/4)(ac) - a³C/4
α=3a²/4, β=-a³C/4 となるように a, θを選ぶ
つまり
a = √(4α/3),
θ = ±arccos(-4β/a³)/3 + 2Nπ/3 {Nは任意整数}
このとき
0 = (ac)^3 -α(ac) +β より x=a*cosθ が解となる。
3次方程式: x^3 - αx + β = 0 の解について
3倍角公式: 4cos^3θ -3cosθ - cos(3θ) = 0
を 4c^3 -3c - C = 0 と書く.
両辺にa^3/4を乗じて
a^3/4*(4c^3 -3c - C) = (ac)^3 - (3a^2/4)(ac) - a^3C/4 = 0
α=3a^2/4, β=-a^3C/4 となるように a, θを選ぶ
つまり
a = √(4α/3),
θ = ±arccos(-4β/a^3)/3 + 2Nπ/3 {Nは任意整数}
このとき
0 = (ac)^3 -α(ac) +β より x=a*cosθ が解となる。
θ°傾けて残り水がπ/3になったとすると、
π∫[t=0→1-sinθ]｛1-(1-t^2)｝dt=π/3
∫[t=0→1-sinθ](2t-t^2)dt=1/3
[t^2-t^3/3](t=1-sinθ)=1/3
(1-sinθ)^2-(1-sinθ)^3/3=1/3
"
ある日本人100人からなる職場では1年間に平均20人に一人が退職する。
退職したら移民で補充するが移民は1年間に平均で10人に一人が退職する。
職場の過半数が移民になるのは何年後か？
"
"
原住民100人からなるある職場では平均して1年間に20人に一人が退職する。
一人の１年間の退職確率は1/20で退職は独立事象とする。
民族を問わず誰かが退職したら同じ人数を移民で補充する。
移民の１年間退職確率は1/10で独立事象とする。
職場の過半数が移民になるのは何年後か？
"
sim <- function(
N=100,
J=100,
I=0){
i=0
while(I < N/2){
i = i + 1 # カウンター
(rJ=rbinom(1,J,1/20)) # 退職原住民数
(rI=rbinom(1,I,1/10)) # 退職移民数
(J=J-rJ) # 原住民職員
(I=I-rI) # 移民職員数（補充前)
(rT=rJ+rI) # 退職総数
I=I+rT # 補充後移民職員数
}
return(i)
}
re=replicate(1e5,sim())
BEST::plotPost(re,xlab='Years')
表が出る確率が1/2のコインを1000回投げたときに表が10回以上連続することが少なくとも１回ある確率を求めよ」
> mean(replicate(10^5,seqn(10)))
[1] 0.38546999999999998
> P10[1000]
[1] 0.38544975241248169
rle
function (x)
{
if (!is.vector(x) && !is.list(x))
stop("'x' must be a vector of an atomic type")
n <- length(x)
if (n == 0L)
return(structure(list(lengths = integer(), values = x),
class = "rle"))
y <- x[-1L] != x[-n]
i <- c(which(y | is.na(y)), n)
structure(list(lengths = diff(c(0L, i)), values = x[i]),
class = "rle")
}
library(gmp)
N=1000
K=10
a=vector('list',N)
for(i in 1:K) a[[i]]=as.bigz(2^(i-1))
for(i in K:(N-1)){
a[[i+1]]=a[[i]]+a[[i-1]]+a[[i-2]]+a[[i-3]]+a[[i-4]]+a[[i-5]]+a[[i-6]]+a[[i-7]]+a[[i-8]]+a[[i-9]]
}
P0=vector('list',N)
for(i in 1:N) P0[[i]]=a[[i]]/2^i
# Pk(n+1)=1/2*P(k-1)(n)
P1=vector('list',N)
P1[[1]]=1/2
for(i in 1:(N-1)) P1[[i+1]]=(1/2)*P0[[i]]
P2=vector('list',N)
P2[[1]]=0
for(i in 1:(N-1)) P2[[i+1]]=(1/2)*P1[[i]]
P3=vector('list',N)
P3[[1]]=0
for(i in 1:(N-1)) P3[[i+1]]=(1/2)*P2[[i]]
P4=vector('list',N)
P4[[1]]=0
for(i in 1:(N-1)) P4[[i+1]]=(1/2)*P3[[i]]
P5=vector('list',N)
P5[[1]]=0
for(i in 1:(N-1)) P5[[i+1]]=(1/2)*P4[[i]]
P6=vector('list',N)
P6[[1]]=0
for(i in 1:(N-1)) P6[[i+1]]=(1/2)*P5[[i]]
P7=vector('list',N)
P7[[1]]=0
for(i in 1:(N-1)) P7[[i+1]]=(1/2)*P6[[i]]
P8=vector('list',N)
P8[[1]]=0
for(i in 1:(N-1)) P8[[i+1]]=1/2*P7[[i]]
P9=vector('list',N)
P9[[1]]=0
for(i in 1:(N-1)) P9[[i+1]]=(1/2)*P8[[i]]
for(i in 1:N) {
P10[i]=list(1-(P0[[i]] + P1[[i]] + P2[[i]] + P3[[i]] + P4[[i]] +
P5[[i]] + P6[[i]] + P7[[i]] + P8[[i]] + P9[[i]])) }
P10[[1000]]
asNumeric(P10[[1000]])
> asNumeric(P10[[1000]])
[1] 0.38544975241248158
> P10[[1000]]
Big Rational ('bigq') :
[1] 4130127273477897798494681823208953122987954337675657485013615586768080707967696405909423852137579237591446526939613263507523948827986893531646240157193872907615641166955214783072447145493481590610836072499227213105120994997891548869020651578128373092635280064104398841562373328900104830268510093352961/10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376
P10[[1000]]
(p=asNumeric(P10[[1000]]))
Rmpfr::mpfr(p,1000)
> Rmpfr::mpfr(p,1000)
1 'mpfr' number of precision 1000 bits
[1] 3.85449752412481583263570428243838250637054443359375e-1
rm(list=ls())
# 表が出る確率が1/2のコインを1000回投げたときに表が10回以上連続することが少なくとも１回ある確率を求めよ
sim <- function(n=10,N=1000){
x=rle(rbinom(N,1,1/2))
x1=x$lengths[x$values==1]
r1 <- any(x1>=n) # 10回以上連続することが少なくとも1回ある
r2 <- sum(x1>=n)==1 # 10回以上連続することが1回だけある
r3 <- max(x1)==n # 表の連続回数の最大値が10回になることが少なくとも1回ある
r4 <- max(x1)==n & sum(x1==n)==1 # 最大値10回が１回だけある
c(r1,r2,r3,r4)
}
re=replicate(1e6,sim())
apply(re,1,mean)
100万回のシミュレーション結果
> apply(re,1,mean)
[1] 0.38601400000000002 0.30114299999999999 0.17037500000000000
[4] 0.15071799999999999
> # 表が連続する最大値が10回の確率
> PP10[[1000]] - PP11[[1000]]
Big Rational ('bigq') :
[1] 1821758352608942392045081404980435252751028506386180152981553957955804306451779919369627290763341161624148375682827473771447204863438275322517352119276475196303665700811594413542122049315965374987419727999162516864425201176898714701858037099287917141519581989266644207027301080510161753883001018598769/10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376
>>259 > Rmpfr::mpfr(asNumeric(PP10[[1000]] - PP11[[1000]]),1e4)
1 'mpfr' number of precision 10000 bits
[1] 1.700180792194284362661704790298244915902614593505859375e-1
0.17でシミュレーションと合致しているので計算は正しいのだろうと思う。
検算希望！（裏口シリツには無理だけどｗｗｗ）
sim <- function(x=0.5,y=0.5){
seg <- function(a,b,...) segments(Re(a),Im(a),Re(b),Im(b),...)
pt <- function(x,y=NULL,...) text(Re(x),Im(x), ifelse(is.null(y),'+',y), ...)
plot(0,type='n',axes=F,ann=F,xlim=c(0,2),ylim=c(0,2),asp=1)
A=0
B=1
C=x+1i*y
pt(A,'A')
pt(B,'B')
pt(C,'C')
seg(A,B)
seg(A,C)
seg(B,C)
sub <- function(pqr){
p=pqr[1];q=pqr[2];r=pqr[3]
P=p
Q=q*(C-A)+(1-q)*(B-A)
R=r*(C-A)
(abs(P-Q) - abs(Q-R))^2 + (abs(P-Q) - abs(P-R))^2
}
par=optim(c(0.5,0.5,0.5),sub)$par
P=par[1]
Q=par[2]*(C-A)+(1-par[2])*(B-A)
R=par[3]*(C-A)
pt(P,'P')
pt(Q,'Q')
pt(R,'R')
seg(P,Q,col=2,lwd=2)
seg(R,Q,col=2,lwd=2)
seg(R,P,col=2,lwd=2)
}
>>253 for(i in K:(N-1)){
a[[i+1]]=a[[i]]
for(j in 1:(K-1)){ a[[i+1]] <- a[[i+1]] + a[[i-j]] }
}
#a[[i+1]]=a[[i]]+a[[i-1]]+a[[i-2]]+a[[i-3]]+a[[i-4]]+a[[i-5]]+a[[i-6]]+a[[i-7]]+a[[i-8]]+a[[i-9]]
# 1000(N)回投げて10(K)回以上表が出る確率
flip <- function(N=1000,K=10){
library(gmp)
library(Rmpfr)
a=vector('list',N)
for(i in 1:K) a[[i]]=as.bigz(2^(i-1))
for(i in K:(N-1)){
a[[i+1]]=a[[i]]
for(j in 1:(K-1)){ a[[i+1]] <- a[[i+1]] + a[[i-j]] }
}
P0=vector('list',N)
for(i in 1:N) P0[[i]]=a[[i]]/2^i
P1=vector('list',N)
P1[[1]]=1/2
for(i in 1:(N-1)) P1[[i+1]]=(1/2)*P0[[i]]
P=vector('list',N)
P[[1]]=P1
for(k in 2:(K-1)){
P[[k]][[1]]=0
for(i in 1:(N-1)) P[[k]][[i+1]]=(1/2)*P[[k-1]][[i]]
}
Ans=1-P0[[N]]
for(k in 1:(K-1)) Ans=Ans-P[[k]][[N]]
ans=Rmpfr::mpfr(asNumeric(Ans),1000)
list(Ans,ans)
}
１０００回のコイントスで連続表の最大値とその確率
# Probability of max(sequential heads)==10 in 1000 coin flips
flip.max <- function(N=1000,K=10){
p11=flip(N,K+1)
p10=flip(N,K)
Ans=p10[[1]]-p11[[1]]
ans=Rmpfr::mpfr(Ans,1000)
list(Ans,ans)
}
flip.max()
flip.max(100,5)
# most probable sequaential heads in 1000 flips
n=3:20
y=sapply(n,function(x) as.numeric(flip.max(1000,x)[[2]]))
plot(n,y,xlab='maximal seq',ylab='p',type='h',col='maroon',lwd=10)
flip.max(1000,8)
flip.max(1000,9)
10 秒速３０ｍで走る長さ３６０ｍの急行列車が、秒速２０ｍで走る長さ４４０ｍの貨物列車に追いついてから追い
抜くまでに何秒かかるか？
（解き方）
〔 〕秒
11 ３６Km 離れた２地点を船で往復した。上りにかかった時間が４時間、下りにかかった時間が３時間だった。
このとき川の流れの速さを求めよ。
（解き方）
〔 〕km/h
12 PとQの二人が、１週１２Km のサイクリングコースを自転車で走る。Pは時速２１Km、Qは時速１２Km で
走行する。Q が走り始めてから１５分後に、Pが同じ方向に走り始めた。PがQに追いつくのは、Pが走り始め
てから何分後か？
（解き方）
〔 〕分後
> sim <- function(){
+ x=rbinom(1000,1,0.5)
+ y=rle(x)
+ max(y$lengths[y$values==1])
+ }
> hmax=replicate(1e6,sim())
> hist(hmax,breaks='scott')
> table(hmax)
hmax
5 6 7 8 9 10 11 12
270 17858 120786 236790 238654 169560 101409 55748
13 14 15 16 17 18 19 20
29148 14687 7610 3790 1821 896 493 225
21 22 23 24 25 26 27 30
139 52 28 14 13 6 1 1
34
1
> data.frame(試行N=N,連続H=unlist(y[1,]),確率P=unlist(y[2,]))
試行N 連続H 確率P
1 2 1 0.5000000
2 3 1 0.5000000
3 4 1 0.4375000
4 5 1 0.3750000
5 6 2 0.3593750
6 7 2 0.3671875
7 8 2 0.3671875
8 9 2 0.3613281
9 10 2 0.3515625
10 11 2 0.3388672
> data.frame(試行N=N,連続H=unlist(y[1,]),確率P=unlist(y[2,]))
試行N 連続H 確率P
1 12 3 0.2849121
2 29 3 0.2743004
3 30 4 0.2708245
4 61 4 0.2559712
5 62 5 0.2561859
6 123 5 0.2475915
7 124 6 0.2471829
8 247 6 0.2424969
9 248 7 0.2423227
10 494 7 0.2396818
11 495 8 0.2395349
12 989 9 0.2380215
13 990 9 0.2380925
コロナ前は、内需型サービス業なのに日本人をぞんざいに扱って、
シナ人ウェルカムの守銭奴ビジネスに熱狂していた業界。
abura(40,39,20) 76 ステップ必要
# its simulation
fn <- function(N,k=1e4){
sim <- function(n){
x=rbinom(n,1,0.5)
y=rle(x)
max(y$lengths[y$values==1])
}
hmax=replicate(k,sim(N))
hist(hmax,breaks='scott',freq=F)
(tbl=table(hmax))
data.frame(H=as.numeric(names(which.max(tbl))), p=max(tbl)/k)
}
fn(100)
fn(1000)
fn(10000)
fn(100000)
fn(1000000)
minStep <- function(x){
a=x[1] ; b=x[2] ; c=x[3]
abr=abura(a,b,c,print=F)
with(abr,min(min_Bigger,min_Smaller))
}
library(numbers)
sim <- function(P=numbers::Primes(100),m=100){
y=0
while(y<m){
x=sort(sample(P,3),dec=T)
y=minStep(x)
}
list(x=x,y=y)
}
sim(m=170)
min_transfer(97,83)
abura(97,83,7)
minStep <- function(x){
a=x[1] ; b=x[2] ; c=x[3]
abr=abura(a,b,c,print=F)
with(abr,min(min_Bigger,min_Smaller))
}
library(numbers)
sim <- function(P=numbers::Primes(100),m=100){
y=0
while(y<m){
x=sort(sample(P,3),dec=T)
y=minStep(x)
}
list(x=x,y=y)
}
sim(m=170)
min_transfer(97,83)
abura(97,83,7)
library(expm)
# 1-(MatrixPower[M,1001].v).v
M=matrix(c(
1,1,1,1,1,1,1,1,1,1,0,
1,0,0,0,0,0,0,0,0,0,0,
0,1,0,0,0,0,0,0,0,0,0,
0,0,1,0,0,0,0,0,0,0,0,
0,0,0,1,0,0,0,0,0,0,0,
0,0,0,0,1,0,0,0,0,0,0,
0,0,0,0,0,1,0,0,0,0,0,
0,0,0,0,0,0,1,0,0,0,0,
0,0,0,0,0,0,0,1,0,0,0,
0,0,0,0,0,0,0,0,1,0,0,
0,0,0,0,0,0,0,0,0,1,2),11,11,byrow=TRUE)
v=c(1,0,0,0,0,0,0,0,0,0,0)
'%.%' <- function(x,y) sum(x*y)
1- (M%^%1001%.%v)%.%v
手持ちの金０のギャンブラーがいるとする。
朝起きてコインを投げて表が出たら１万円貰える。
裏が出れば１万円を払う。手元に金がないときは借金として記録される。金利はつかない。
１年間これを行って黒字であった日数を記録して精算して持ち金を０にリセットする。閏日はギャンブルなしとして
これを毎年繰り返したときの黒字の日数の分布は年数を増やすと正規分布になるか？
flip <- function(N=1000,n=10){ # n+ heads in N coin flips
library(gmp)
library(expm)
'%.%' <- function(x,y) sum(x*y)
M=cbind(rbind(rep(1,n),diag(1,n,n)),c(rep(0,n),2))
v=as.vector.bigq(c(1,rep(0,n)))
P=as.bigq((M/2)%^%N %*% v)[n+1]
list(P=P,p=as.numeric(P))
}
flip(1000,10)$p
flip(1000,10)$p - flip(1000,11)$p
flip.max <- function(N=1000,n=10){
P=flip(N,n)$P - flip(N,n+1)$P
list(P=P,p=as.numeric(P))
}
sapply(11:13, function(x) flip.max(1e4,x)$p)
sapply(14:16, function(x) flip.max(1e5,x)$p)
sapply(17:19, function(x) flip.max(1e6,x)$p)
sapply(21:23, function(x) flip.max(1e7,x)$p)
sapply(24:26, function(x) flip.max(1e8,x)$p)
分数表示版がようやく完成。
Flip <- function(N=100,n=5){ # n+ heads in N coin flips
library(gmp)
library(expm)
'%.%' <- function(x,y) sum(x*y)
M=as.bigq(cbind(rbind(rep(1,n),diag(1,n,n)),c(rep(0,n),2)))
v=as.vector.bigq(c(1,rep(0,n)))
d=diag(1,n+1,n+1)
for(i in 1:N) d=d%*%M/2
P=(d%*%v)[[n+1]]
list(P=P,p=as.numeric(P))
}
Flip(1000,10)
Flip.max <- function(N=1000,n=10){
P=Flip(N,n)$P - Flip(N,n+1)$P
list(P=P,p=as.numeric(P))
}
Flip.max(1000,10)
コインを1000回投げて表が連続する回数の最大が10回である確率
1821758352608942392045081404980435252751028506386180152981553957955804306451779919369627290763341161624148375682827473771447204863438275322517352119276475196303665700811594413542122049315965374987419727999162516864425201176898714701858037099287917141519581989266644207027301080510161753883001018598769/10715086071862673209484250490600018105614048117055336074437503883703510511249361224931983788156958581275946729175531468251871452856923140435984577574698574803934567774824230985421074605062371141877954182153046474983581941267398767559165543946077062914571196477686542167660429831652624386837205668069376
コインを1億回投げて表が連続する回数の最大数を当てる賭けをするにはいくつに賭けるのが最も勝利確率が高いか？
さすがに分数表示は無理だが、その確率は 0.2493603162 とわりと高い。
binom(n, p) ～ N((n+1)p -1/2, (n+1)p(1-p))
>>277 標準化するとJefferey分布になった。
手持ちの金0のギャンブラーがいるとする。
朝起きて1回コインを投げて表が出たら1万円貰える。
裏が出れば1万円を払う。手元に金がないときは借金として記録される。金利は0
1年(365日とする)間これを行って黒字であった日数を記録して精算して持ち金を0にリセットする。
これを毎年繰り返す。1年に300日以上黒字である確率は？
１－300/365かなという、直感に反するな。
rm(list=ls())
source('toolmini.R')
options(digits=10)
ngon
n=7
p=ngon(n,axis=T)
seg(p[4],0.5,lty=2)
seg(p[4],p[1],lty=2)
abs(p[4]-0.5) # height
abs(p[4]-p[1])
rm(list=ls())
options(digits=10)
# draw regular polygon
ngon <- function(n,digit=TRUE,axis=FALSE,cex=1,...){
r=exp(2*pi/n*1i)
p=complex(n)
for(i in 1:(n+1)) p[i]= (1-r^i)/(1-r)
plot(p,bty='l',type='l',axes=axis, ann=FALSE,asp=1)
points(1/(1-r),pch='.')
if(digit) text(Re(p),Im(p),1:n,cex=cex)
if(axis){axis(1) ; axis(2)}
invisible(p)
}
n=7
# (1/2)/R=sin((2pi/n)/2)
(R=sin(pi/n)/2)
p=ngon(n,axis=T)
seg(p[4],0.5,lty=2)
seg(p[4],p[1],lty=2)R=
h=abs(p[4]-0.5) # height
m=abs(p[4]-p[1]) # max diagnonal length
m>h
options(digits=10)
# draw regular polygon
ngon <- function(n,digit=TRUE,axis=FALSE,cex=1,...){
r=exp(2*pi/n*1i)
p=complex(n)
for(i in 1:(n+1)) p[i]= (1-r^i)/(1-r)
# plot(p,bty='l',type='l',axes=axis, ann=FALSE,asp=1)
# points(1/(1-r),pch='.')
# if(digit) text(Re(p),Im(p),1:n,cex=cex)
# if(axis){axis(1) ; axis(2)}
invisible(p)
}
# draw segment of complex a to complex b
seg <- function(a,b,...){
segments(Re(a),Im(a),Re(b),Im(b),...)
}
# draw text y at complex x
pt <- function(x,y=NULL,...){
text(Re(x),Im(x), ifelse(is.null(y),'+',y), ...)
}
n=7
# (1/2)/R=sin((2pi/n)/2)
(R=sin(pi/n)/2)
p=ngon(n,axis=T)
#seg(p[4],p[1],lty=2)
m=which.max(abs(p[1]-p[1:n])) # maximal diagnonal vertex
mdl=abs(p[1]-p[m]) # max. diagnonal length
top=1/2+1i*Im(p[floor(median(n))] )
# seg(0.5,top)
height=Im(top)
mdl > height
'%&%' <- function(x,y) paste0(x,y)
> '√2 =' %&% sqrt(2) %&% ', π = ' %&% pi
[1] "√2 =1.4142135623731, π = 3.14159265358979"
random <- function(n,char=c(LETTERS,letters,0:9)){
re=paste0(sample(char,n),collapse='')
cat(re,'\n')
invisible(re)
}
random()
> random(16)
PLZrvwnDVbmC4fWz
> random(100)
Error in sample.int(length(x), size, replace, prob) :
cannot take a sample larger than the population when 'replace = FALSE'
エラーが出たｗ
デバッグ
random <- function(n=16,char=c(LETTERS,letters,0:9)){
rep=ifelse(n>length(char),TRUE,FALSE)
re=paste0(sample(char,n,replace=rep),collapse='')
cat(re,'\n')
invisible(re)
}
> random()
ldWENnFATyQbBve7fXMSopCKq8r5guVY
> random(100)
ipb2KH88oGyrTGV7KCXU3Aez4PaFztnlI2IiHQqJbFlI8r3yYjDh9kKqhOLZUzuNjULlZBs6NNj4sFLqjeZ14bT3pROnNr6kYG8x
完成！
１辺の長さ１の正７角形の高さ
(sin(2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - (cos(4*2*pi/7)*sin(2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) - sin(4*2*pi/7)/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2) + (cos(2*pi/7)* sin(4*2*pi/7))/((1 - cos(2*pi/7))^2 + sin(2*pi/7)^2))
外接円の半径は
(1/2)*/sin(pi/7))
# draw regular polygon
ngon <- function(n,digit=TRUE,cex=1,...){
r=exp(2*pi/n*1i)
p=complex(n)
for(i in 1:(n+1)) p[i]= (1-r^i)/(1-r)
plot(p,bty='l',type='l',ann=FALSE,asp=1,...)
points(1/(1-r),pch='.')
if(digit) text(Re(p),Im(p),1:n,cex=cex)
invisible(p)
}
# draw segment of complex a to complex b
seg <- function(a,b,...){
segments(Re(a),Im(a),Re(b),Im(b),...)
}
# draw text y at complex x
pt <- function(x,y=NULL,...){
text(Re(x),Im(x), ifelse(is.null(y),'+',y), ...)
}
# draw circle
cir <- function(x, y, r, ...){
theta <- seq(-pi, pi, length=100)
lines(x + r*cos(theta), y + r*sin(theta), ...)
}
Cir <- function(z,r,...){
cir(Re(z),Im(z),r,...)
}
# R*sin(pi/n)=(1/2)*side
n=7 ; side=1
(R=(1/2)*side/sin(pi/n))
manhole <- function(n,...){
p=ngon(n,...)
r=(1/2)/sin(pi/n) # Radius of circumsribing circle
C=(1/2+1i*(1/2)*sqrt(4*r^2-1)) # its enter
Cir(C,r,lty=3,col=8)
m=which.max(abs(p[1]-p[1:n])) # maximal diagnonal vertex
seg(p[1],p[m],col='blue')
(mdl=abs(p[1]-p[m])) # max. diagnonal length
top=1/2+1i*Im(p[floor( median(1:n) )] )
seg(0.5,top,col='red')
(height=Im(top))
list(対角線=mdl,高さ=height, 落下= mdl > height,R=R)
}
n=7
(a=manhole(n,axes=F))
(side=a[[1]]/a[[2]]) # 落下しない正n多角形の辺の長さ
(1/2)*side/sin(pi/n) # その外接円の半径
>>294 正多角形なので重心＝外心ゆえ、連立方程式を解かずに拡張点の平均を求めれる方が早かった。
manhole <- function(n,...){
p=ngon(n,...)
r=(1/2)/sin(pi/n) # Radius of circumscribing circle
C= (1/2+1i*(1/2)*sqrt(4*r^2-1)) # its center == mean(p[1:7])
Cir(C,r,lty=3,col=8)
pt(mean(p[1:7]))
m=which.max(abs(p[1]-p[1:n])) # maximal diagonal vertex
seg(p[1],p[m],col='blue')
(mdl=abs(p[1]-p[m])) # max. diagnonal length
top=1/2+1i*Im(p[floor( median(1:n) )] )
seg(0.5,top,col='red')
(height=Im(top))
list(対角線=mdl,高さ=height, 落下= mdl > height,外接円半径=r)
}
n=7
(a=manhole(n,axes=F))
(side=a[[1]]/a[[2]]) # 落下しない正n多角形の辺の長さ
(1/2)*side/sin(pi/n) # その外接円の半径
nを6以上の自然数とするとき
a+b+c=n , 0<a<b<c を満たす自然数a,b,cの組(a,b,c)の個数をnの式で表すことはできますか。
f <- function(n=10,verbose=FALSE){
y=NULL
for(a in 1:(n-2)){
for(b in a:(n-1)){
for(c in b:n){
if(a+b+c==n & a!=b & b!=c & c!=a) y=rbind(y,c(a,b,c))
}
}
}
if(verbose) print(y)
return(nrow(y))
}
f(15,verbose = T)
f=Vectorize(f)
n=6:200
y=f(n)
plot(n,y,ylab='count')
dat=cbind(6:200,y)
"
(n-1)(n-5)/12 + d_2 /4 + d_3 /3
d_2 = {1 + (-1)^n}/2 = (nが偶数のとき1, nが奇数のとき0)
d_3 = {1 + ω^n + (ω~)^n}/3 = (nが3の倍数のとき1, 他は0)
"
f11 <- function(n){
d_2=ifelse(n%%2==0,1,0)
d_3=ifelse(n%%3==0,1,0)
(n-1)*(n-5)/12 + d_2/4 + d_3/3
}
Y=f11(n)
lines(n,Y,col=2,lwd=3)
(n-1)(n-5)/12 + d_2 /4 + d_3 /3 = (1/12)^n2 - (1/2)*n + 5/12 + d_2/4 + d_3/3
> nls(Y ~ a*x^2+b*x+c, start=c(a=1,b=1,c=1))
Nonlinear regression model
model: Y ~ a * x^2 + b * x + c
data: parent.frame()
a b c
0.08333384 -0.50014021 0.66082814
residual sum-of-squares: 7.915997
Number of iterations to convergence: 1
Achieved convergence tolerance: 5.815117e-08
1/12=0.83333
1/2=0.5
5/12 + .... = 0.4166666667
上出来の近似
回帰式の値を四捨五入してみると
> data.frame(n,Y,round(Y.nls))
n Y round.Y.nls.
1 6 1 1
2 7 1 1
3 8 2 2
4 9 3 3
5 10 4 4
6 11 5 5
7 12 7 7
8 13 8 8
9 14 10 10
10 15 12 12
...
187 192 2977 2977
188 193 3008 3008
189 194 3040 3040
190 195 3072 3072
191 196 3104 3104
192 197 3136 3136
193 198 3169 3169
194 199 3201 3201
195 200 3234 3234
6から200まで、すべて一致している。
curve(-cos(x),-pi,pi,bty='l',ylim=c(-1,1),ann=F)
wine <- function(x,z) -cos(sqrt(x^2+z^2))
N=1e7
x=runif(N,-pi,pi)
y=runif(N,-1,1)
z=runif(N,-pi,pi)
(2*pi)*2*(2*pi) * mean(y >wine(x,z) & x^2+z^2<pi^2 )
N=1e5
x=runif(N,-pi,pi)
y=runif(N,-1,1)
z=runif(N,-pi,pi)
w=NULL
counter=0
for(i in 1:N){
if(y[i]>wine(x[i],z[i]) & x[i]^2+z[i]^2<pi^2 ){
w=rbind(w,c(x[i],y[i],z[i]))
counter=counter+1
}
}
(2*pi)*2*(2*pi)*counter/N
rgl::plot3d(w[,1],w[,2],w[,3],col='maroon',asp=1)
rm(list=ls())
source('toolmini.R')
# full volume
f<- function(x) -cos(x) # == sin(x-pi/2) == -cos(x)
curve(f(x),-pi,pi,ylab='-cos(x)')
seg(-1i,-0.5i,col=8)
seg(0-0.5i,pi-acos(-0.5)-0.5i,col=8)
seg(-1i,pi-acos(-0.5)-1i,col=8,lty=3)
seg(pi-acos(-0.5)-1i,pi-acos(-0.5)-0.5i,col=8,lty=3)
pt(-0.5i,'h')
pt(pi-acos(-0.5)-0.5i,'(π-acos(h))')
A <- function(x) pi*(pi-acos(x))^2
# ∫[-1,-1] pi*(pi-acos(h))^2 dh
integrate(A,-1,1)$value ; pi*(pi^2-4) # π(π^2-4)
#
回転正弦曲面のグラフ化
fy=function(x,z){
ss=x^2+z^2
if(ss<pi^2) -cos(sqrt(x^2+z^2))
else NA
}
fy=Vectorize(fy)
x=z=seq(-pi,pi,length=300)
y=outer(x,z,fy)
rgl::persp3d(x,z,y,col='maroon')
intsect <- function(a,b,c,d)){
a1=Re(a) ; a2=Im(a)
b1=Re(b) ; b2=Im(b)
p=(b1-b2)/(a1-a2)
# y-a2=p*(x-a1)
# p*x - y = p*a1 - a2
c1=Re(c) ; c2=Im(c)
d1=Re(d) ; d2=Im(d)
q=(d1-d2)/(c1-c2)
# y-c2=q*(x-c1)
# q*x - y = q*c1 - c2
M=matrix(c(p,-1,q,-1),2,2,b=T)
v=c(p*a1-a2, q*c1-c2)
s=solve(M,v)
s[1]+1i*s[2]
}
三角形ABCの内部に点DをとりADとBC、BDとAC、CDとABの交点を各々E,F,Gとする。
このとき点Dをうまく選べば三角形EFGを任意の三角形に相似にすることが可能であるという命題は真か偽か？
# ある点が三角形の内部にあるか？
oup <- function(A,B){ # 外積 outer prodct
Ax=A[1];Ay=A[2];Az=A[3]
Bx=B[1];By=B[2];Bz=B[3]
c(Ay*Bz-Az*By, Az*Bx-Ax*Bz, Ax*By-Ay*Bx)
}
# 二次元なので Z軸の値の正負のみが必要
# Ax=Re(a);Ay=Im(a);Az=0
# Bx=Re(b);By=Im(b);Bz=0
# c(Ay*Bz-Az*By, Az*Bx-Ax*Bz, Ax*By-Ay*Bx)
opc <- function(a,b){ # outer product on complex plane
Re(a)*Im(b)-Im(a)*Re(b)
}
align <- function(ABC){ # ベクトルABとベクトルACの外積が0なら3点は直線上にある
opc(ABC[2]-ABC[1],ABC[3]-ABC[1])==0
}
in3 <- function(P,A,B,C){ # is P inside triangle ABC?
sum(opc(B-A,P-A)>0,opc(C-B,P-B)>0,opc(P-A,C-A)>0)%%3==0
# 右ねじ外積の方向がZ軸で全て正か全て負かで三角形の内部と確認
}
100円玉3個と50円玉2個を同時に投げて、100円玉の表の出た枚数をX、50円玉の表を出た枚数をYとする。（X.Y)の2次元分布を書き、X.Yが独立であるかどうかを言いなさい。
当たり前のことを確認するのはわりと面倒
dec2nw <- function(num, N, digit = 4){
r=num%%N
q=num%/%N
while(q > 0 | digit > 1){
r=append(q%%N,r)
q=q%/%N
digit=digit-1
}
return(r)
}
(z=t(sapply(0:31, function(x) dec2nw(x,2,5))))
f=function(x) c(sum(x[1:3]),sum(x[4:5]))
xy=apply(z,1,f)
x=xy[1,] ; y=xy[2,]
table(x)
table(y)
px=as.bigq(table(x)/32)
py=as.bigq(table(y)/32)
outer(px,py)
gr=expand.grid(0:3,0:2)
g=function(x){
count=0
for(i in 1:32) count=count+(x[1]==xy[1,i] & x[2]==xy[2,i])
return(count)
}
as.bigq(matrix(apply(gr,1,g),nrow=4,ncol=3)/32)
なるほどね
>>
イギリス+560(7/23)
イタリア+252(7/24)
香港+123(7/24)
韓国+113(7/24)
中国+34(7/24)
マレーシア+21(7/24)
タイ+8(7/23)
ベトナム+7(7/23)
台湾+3(7/24)
日本+777(7/24)
やっぱり低学歴には何をやらせてもダメだな
他より劣っていても平気でいられる感覚が染み付いてる
tan(θ)*(x-x0)+y0+cos(sqrt(x^2+z0^2))=0
がxについて解けない。
コロナ対策で様々な設備投資をしたら、それはそれで赤字。
コロナ患者を受け入れれば受け入れるほど赤字になる、と病院関係者が訴えてるが、安倍政権はGOTOキャンペーンに躍起。
Gacha <- function(p){ # p: probability of each Gacha item , sum(p) <=1
if(sum(p)>1) warning("sum(p)>1")
sum.rev <- function(x){ # i,j,k -> 1/(p[i]+p[j]+p[k])
n=length(x)
s=numeric(n)
for(i in 1:n) s[i]=p[x[i]]
1/sum(s)
}
n=length(p)
re=numeric(n)
for(i in 1:n) re[i]=(-1)^(i-1)*sum(apply(combn(n,i),2,sum.rev))
sum(re)
}
Gacha.fm <- function(p,write=FALSE){
n=length(p)
par=letters[1:n]
fm <- function(v){
nv=length(v)
re=character(nv)
for(j in 1:nv) re[j]=par[v[j]]
s=paste(re,collapse='+')
if(nv==1) paste0('1/',s)
else paste0('1/(',s,')')
}
fm1 <- function(mat){
paste(apply(mat,2,fm),collapse='+')
}
re=list()
for(i in 1:n) re[[i]]=fm1(combn(n,i))
re1=re[[1]]
for(i in 2:(n-1)){
re1=c(re1,ifelse(i%%2,' + ',' - '),'{',re[[i]],'}')
}
output=paste(paste(re1,collapse=""),ifelse(n%%2,'+','-'), re[[n]])
cat(output,'\n')
if(write) write(output,'output.txt')
invisible(output)
}
rm(list=ls())
library(gmp)
dec2nw <- function(num, N, digit = 4){
r=num%%N
q=num%/%N
while(q > 0 | digit > 1){
r=append(q%%N,r)
q=q%/%N
digit=digit-1
}
return(r)
}
is.plus<-function(x) (sum(x)+sum(x-1))>0 # is plus balance?
fn <- function(n){
balance=0
for(i in 1:(2^n)){
balance=balance+is.plus(dec2nw(i-1,2,n))
}
p=as.bigq(balance/2^n)
list(p,as.numeric(p))
}
fn(8)
n=1:15*2
re=lapply(n,fn)
θ傾けたワイングラスの支柱方向に積分
回転軸をy軸にしてy=tの断面での関数
x=(t-y0)/tan(θ) + x0
z=sqrt(acos(-t)+x^2)
x=z=seq(-pi,pi,0.1)
f<-function(x,z) -cos(sqrt(x^2+z^2))
f=Vectorize(f)
y=outer(x,z,f)
contour(x,z,y)
abline
x=z=seq(-pi,pi,0.1)
f<-function(x,z) -cos(sqrt(x^2+z^2))
f=Vectorize(f)
y=outer(x,z,f)
t=runif(1,-1,1)
contour(x,z,y,level=t)
abline(v=(t-y0)/tan(θ)+ x0)
>>313 theta=pi/19
x=z=seq(-pi,pi,0.1)
f<-function(x,z) -cos(sqrt(x^2+z^2))
f=Vectorize(f)
y=outer(x,z,f)
(t=runif(1,-1,1))
contour(x,z,y,level=t)
z0=0
df <- function(x) (x*sin(sqrt(x^2 + z0^2)))/sqrt(x^2 + z0^2)
df=Vectorize(df)
x0=uniroot(function(x) df(x)-tan(theta),c(pi/2,pi+1e-12),tol=1e-12)$root
y0=f(x0,0)
abline(v=(t-y0)/tan(theta)+ x0)
moon <- function(m,r=1){ # moon area above horizon
x1= -sqrt(r^2-m^2)
x2= sqrt(r^2-m^2)
if(m>0) {
a=function(x) sqrt(r^2-x^2)-m
integrate(a,x1,x2)$value
}else{
b=function(x) m+sqrt(r^2-x^2)
pi*r^2-integrate(b,x1,x2)$value
}
}
#
#
TWG <- function(theta){ # Tilted Wine Glass (0<= theta < pi/4)
f<-function(x,z) -cos(sqrt(x^2+z^2)) # curved surface of wine glass
f=Vectorize(f)
df <- function(x,z0=0) (x*sin(sqrt(x^2 + z0^2)))/sqrt(x^2 + z0^2) # f'
df=Vectorize(df)
# (x0,y0) upper coordinates of wine
x0=uniroot(function(x) df(x)-tan(theta),c(pi/2,pi+1e-12),tol=1e-12)$root
y0=f(x0,0)
# (u0x,u0y) lower coordinates of wine
u0x=uniroot(function(x,z0=0) tan(theta)*(x-x0)+y0+cos(sqrt(x^2+z0^2)), c(-pi,pi/4))$root
u0y=f(u0x,0)
moon <- function(m,r=1){ # return area of demi-circle above y=m
x1= -sqrt(r^2-m^2)
x2= sqrt(r^2-m^2)
if(m>0) {
a=function(x) sqrt(r^2-x^2)-m
integrate(a,x1,x2)$value
}else{
b=function(x) m+sqrt(r^2-x^2)
pi*r^2-integrate(b,x1,x2)$value
}
}
area <- function(t){ # when y=t
r=acos(-t) # t -> radius
xL=(t-y0)/tan(theta)+ x0 # surface border
if(t>u0y){ # defected moon
moon(xL,r)
}else{
return(pi*r^2) # full moon
}
}
Area=Vectorize(area)
integrate(Area, -1,y0)$value
}
TWG(0)
TWG(pi/19)
WG <- function(deg) TWG(deg*pi/180)
WG(0)
WG(9)/WG(0)
WG(10)/WG(0)
WG=Vectorize(WG)
uniroot(function(x) WG(x)/WG(0)-1/2,c(9,10))$root
tan(θ)*(x-pi+asin(tan(θ)))+cos(asin(tan(θ)))+cos(x)=0
θは定数でxについて解く必要がある。
>>320 α*x + β + cos(x) = 0
α=taｎθ
β=-pi*taｎθ+taｎθasin(taｎθ) + cos(asin(taｎθ))
α*x + β + cos(x) = 0
α=tanθ
β=-pi*tanθ+tanθasin(tanθ) + cos(asin(tanθ))
新型コロナウイルス対策 in 医者板 Part.13
http://2chb.net/r/hosp/1594803201/712 712 名前：卵の名無しさん[sage] 投稿日：2020/07/30(木) 22:57:30.04 ID:ym0dFMP6
このまま行くと超過死亡また増えるね
①発熱→おことわり
②コロナ→赤字になるからやらない
③逃げられない感染指定、都立、国立→おなかいっぱいになったら崩壊
④日本全国医療機関患者激減→経営困難
⑤具合悪くてもコロナの恐怖で病院控える→手遅れになり死亡
⑥介護施設クラスター→受け入れ先無し
⑦コロナによる死亡
⑤が一番の恐怖でコロナより死亡が増える
④は国が救済しないと破綻する所が出てくる
②は一波の時さんざんな目にあった→スタッフの体勢が準備出来てません、などなど。
歌舞伎町のクラスターの時点で全自動さっさと認可して二桁多い検査と隔離してたら
こんなに経済に負担が掛からなかったのに、重傷者まだ少ないし、政府は投げやり
コロナが増える＝さまざまな経済や医療やナイナス要素しかない
コロナはやっぱクラスター出たら全力で掃討しないと結局みんな損する
でも得する一部の投資家や利権などなど。
自民から民主になろうが利権は継続する糸引いてる富豪が変わらない
まあ資本主義と格差社会の象徴だな。コロナはここを突いてくる厄介な敵
integral π (π - cos^(-1)(x))^2 dx = π (2 π sqrt(1 - x^2) - 2 (sqrt(1 - x^2) + π x) cos^(-1)(x) + (π^2 - 2) x + x cos^(-1)(x)^2) + 定数
"正弦回転体のワイングラスにストローを刺して半分飲む"
x=z=seq(-pi,pi,0.01)
f<-function(x,z=0) -cos(sqrt(x^2+z^2))
f=Vectorize(f)
curve(f(x),-pi,pi,ann=F,bty='n',axes=F)
segments(x,f(x),x,1,col='orange')
lines(x,f(x),lwd=2)
juice <- function(h){
# v <- function(x)pi*( 2*pi*sqrt(1-x^2)-2*(sqrt(1-x^2)+pi*x)*acos(x)
# +(pi^2-2)*x+x*(acos(x)^2) )
# v(-1+h) - v(-1) , v(-1) = 2*pi
# v(h-1) - 2*pi
pi*( 2*pi*sqrt(1- (h-1)^2)-2*(sqrt(1- (h-1)^2)+pi* (h-1))*acos( (h-1))
+(pi^2-2)* (h-1)+ (h-1)*(acos( (h-1))^2) ) -2*pi
}
juice(2) ; pi*(pi^2-4) # π(π^2-4)
uniroot( function(h) juice(h)/juice(2) - 1/2, c(0,2), tol = 1e-12)$root/2
library(tidyverse)
6 %>% rerun(1:2) %>% expand.grid
'%&%' <- function(x,y) paste0(x,y)
eval(str2lang("expand.grid(" %&% paste0(rep("1:2",6),collapse=',') %&% ")"))
expand.grid(replicate(6,1:2,simplify = FALSE))
rerun(6,1:2)
10 %>% rerun(rnorm(5))
# 正方形の対角線の座標から残りの対角線の座標を返す
dia <- function(a,b){
a1=a[1] ; a2=a[2]
b1=b[1] ; b2=b[2]
A=a1+1i*a2
B=b1+1i*b2
AB=B-A
th=Arg(AB)
r=abs(AB)
R=r/sqrt(2)
THc=th+pi/4
THd=th-pi/4
C=R*(cos(THc)+1i*sin(THc))+A
D=R*(cos(THd)+1i*sin(THd))+A
c1=Re(C) ; c2=Im(C)
d1=Re(D) ; d2=Im(C)
list(c(c1,c2),c(d1,d2))
}
正方形の対角線の座標から残りの対角線の座標を返す
dia <- function(a,b){
a1=a[1] ; a2=a[2]
b1=b[1] ; b2=b[2]
A=a1+1i*a2
B=b1+1i*b2
AB=B-A
th=Arg(AB)
r=abs(AB)
R=r/sqrt(2)
THc=th+pi/4
THd=th-pi/4
C=R*(cos(THc)+1i*sin(THc))+A
D=R*(cos(THd)+1i*sin(THd))+A
c1=Re(C) ; c2=Im(C)
d1=Re(D) ; d2=Im(D)
list(c(c1,c2),c(d1,d2))
}
dia(c(2,2),c(1,1))
交点の座標を返す
intsect <- function(a,b,c,d)){
a1=Re(a) ; a2=Im(a)
b1=Re(b) ; b2=Im(b)
p=(b1-b2)/(a1-a2)
# y-a2=p*(x-a1)
# p*x - y = p*a1 - a2
c1=Re(c) ; c2=Im(c)
d1=Re(d) ; d2=Im(d)
q=(d1-d2)/(c1-c2)
# y-c2=q*(x-c1)
# q*x - y = q*c1 - c2
M=matrix(c(p,-1,q,-1),2,2,b=T)
v=c(p*a1-a2, q*c1-c2)
s=solve(M,v)
s[1]+1i*s[2]
}
# 正方形の対角線の複素座標から残りの対角線の座標を返す
dia <- function(a,b){
if(is.complex(a)){
a1=Re(a) ; a2=Im(a)
}else{
a1=a[1] ; a2=a[2]
}
if(is.complex(b)){
b1=Re(b) ; b2=Im(b)
}else{
b1=b[1] ; b2=b[2]
}
A=a1+1i*a2
B=b1+1i*b2
AB=B-A
th=Arg(AB)
r=abs(AB)
R=r/sqrt(2)
THc=th+pi/4
THd=th-pi/4
C=R*(cos(THc)+1i*sin(THc))+A
D=R*(cos(THd)+1i*sin(THd))+A
if (is.complex(a)) return(list(C,D))
else{
c1=Re(C) ; c2=Im(C)
d1=Re(D) ; d2=Im(D)
return(list(c(c1,c2),c(d1,d2)))
}
dia(c(2,2),c(1,1))
dia(0i,3+3i)
# 正方形の対角線の複素座標から残りの対角線の座標を返す
dia <- function(a,b){
if(is.complex(a)){
a1=Re(a) ; a2=Im(a)
}else{
a1=a[1] ; a2=a[2]
}
if(is.complex(b)){
b1=Re(b) ; b2=Im(b)
}else{
b1=b[1] ; b2=b[2]
}
A=a1+1i*a2
B=b1+1i*b2
AB=B-A
th=Arg(AB)
r=abs(AB)
R=r/sqrt(2)
THc=th+pi/4
THd=th-pi/4
C=R*(cos(THc)+1i*sin(THc))+A
D=R*(cos(THd)+1i*sin(THd))+A
if (is.complex(a)) return(list(C,D))
else{
c1=Re(C) ; c2=Im(C)
d1=Re(D) ; d2=Im(D)
return(list(c(c1,c2),c(d1,d2)))
}
}
dia(c(2,2),c(1,1))
dia(0i,3+3i)
"AB=4,BC=5,CA=6の△ABCの周および内部の領域をDとする。
D内に以下の条件を全て満たすように2つの正方形SとTを配置したい。
Sの一辺の長さsを求めよ。ただしTの一辺の長さをtとすると、s≧tである。
(i)SとTはともにDに含まれる。
(ii)SはTの外部にあるか、またはSとTは外接している。
(iii)条件(i)(ii)を満たすS,Tの配置は様々であるが、その中で積stが最大である。
"
rm(list=ls())
source('toolmini.R')
# 正方形の対角線の複素座標から残りの対角線の座標を返す
dia <- function(a,b){
if(is.complex(a)){
a1=Re(a) ; a2=Im(a)
}else{
a1=a[1] ; a2=a[2]
}
if(is.complex(b)){
b1=Re(b) ; b2=Im(b)
}else{
b1=b[1] ; b2=b[2]
}
A=a1+1i*a2
B=b1+1i*b2
AB=B-A
th=Arg(AB)
r=abs(AB)
R=r/sqrt(2)
THc=th+pi/4
THd=th-pi/4
C=R*(cos(THc)+1i*sin(THc))+A
D=R*(cos(THd)+1i*sin(THd))+A
if (is.complex(a)) return(list(C,D))
else{
c1=Re(C) ; c2=Im(C)
d1=Re(D) ; d2=Im(D)
return(list(c(c1,c2),c(d1,d2)))
}
}
# ある点P（複素点)が三角形ABCの内部にあるか？
opc <- function(a,b){ # outer product on complex plane
Re(a)*Im(b)-Im(a)*Re(b)
}
in3 <- function(P,A,B,C){ # is P inside triangle ABC?
sum(opc(B-A,P-A)>0,opc(C-B,P-B)>0,opc(P-A,C-A)>0)%%3==0
# 右ねじ外積の方向がZ軸で全て正か全て負かで三角形の内部と確認
}
# ある点Pが四角形の内部にあるか
in4 <- function(P,A,B,C,D){
in3(P,A,B,C) | in3(P,A,C,D)
}
sim <- function(z=c(3,3,2.5,1, 1,1,1.2,0.5),print=FALSE){
s1x=z[1] ; s1y=z[2] ; s2x=z[3] ; s2y=z[4]
t1x=z[5] ; t1y=z[6] ; t2x=z[7] ; t2y=z[8]
s1=s1x+1i*s1y ; s2=s2x+1i*s2y
t1=t1x+1i*t1y ; t2=t2x+1i*t2y
# s1,s2,t1,t2が三角形の外部なら0を返す
if(!(in3(s1,A,B,C) & in3(s2,A,B,C) & in3(t1,A,B,C) & in3(t2,A,B,C))) return(0)
# 残りの対角点が三角形の外部なら0を返す
if(all(unlist(lapply(dia(s1,s2),function(x) in3(x,A,B,C))))==FALSE) return(0)
if(all(unlist(lapply(dia(t1,t2),function(x) in3(x,A,B,C))))==FALSE) return(0)
s34=dia(s1,s2)
s3=s34[[1]] ; s4=s34[[2]]
t34=dia(t1,t2)
t3=t34[[1]] ; t4=t34[[2]]
# 正方形が重なっていれば０を返す
if(any(in4(s1,t1,t3,t2,t4), in4(s2,t1,t3,t2,t4), in4(s3,t1,t3,t2,t4),in4(s4,t1,t3,t2,t4),
in4(t1,s1,s3,s2,s4), in4(t2,s1,s3,s2,s4), in4(t3,s1,s3,s2,s4),in4(t4,s1,s3,s2,s4)
)){ return(0)
}else{
if(print){
plot(NULL,xlim=c(0,4),ylim=c(0,6),ann=F,bty='l',asp=1)
A=0i
B=4+0i
C=27/8+1i*sqrt(36-(27/8)^2)
seg(A,B) ; seg(A,C) ; seg(B,C)
pt(A,'A') ; pt(B,'B') ; pt(C,'C')
pt(s1,'s1') ; pt(s2,'s2') ; pt(t1,'t1') ; pt(t2,'t2')
pt(s3,'s3') ; pt(s4,'s4')
pt(t3,'t3') ; pt(t4,'t4')
par(lwd=2)
seg(s1,s3,col=2) ;seg(s2,s4,col=2) ; seg(s2,s3,col=2) ;seg(s1,s4,col=2)
seg(t1,t3,col=2) ;seg(t2,t4,col=2) ; seg(t2,t3,col=2) ;seg(t1,t4,col=2)
par(lwd=1)
}
s=abs(s1-s3)
t=abs(t1-t3)
if(s<t) return(0)
else return(s*t)
}
}
sim(print=T)
(opt=optim(par=c(3,3,2.5,1, 1,1,1.2,0.5),fn=sim,control=list(fnscale=-1,reltol=1e-16)))
sim(opt$par,print=T)
出来上がり
# 平行なときはNAを返す
# 交点の座標を返す
intsect <- function(a,b,c,d){
a1=Re(a) ; a2=Im(a)
b1=Re(b) ; b2=Im(b)
p=(a2-b2)/(a1-b1)
# y-a2=p*(x-a1)
# p*x - y = p*a1 - a2
c1=Re(c) ; c2=Im(c)
d1=Re(d) ; d2=Im(d)
q=(c2-d2)/(c1-d1)
# y-c2=q*(x-c1)
# q*x - y = q*c1 - c2
if(p==q) return(NA)
else{
M=matrix(c(p,q,-1,-1),nrow=2)
v=c(p*a1-a2, q*c1-c2)
s=solve(M,v)
s[1]+1i*s[2]}
}
# 交点の座標を返す
intsect <- function(a,b,c,d){
a1=Re(a) ; a2=Im(a)
b1=Re(b) ; b2=Im(b)
p=(a2-b2)/(a1-b1)
# y-a2=p*(x-a1)
# p*x - y = p*a1 - a2
c1=Re(c) ; c2=Im(c)
d1=Re(d) ; d2=Im(d)
q=(c2-d2)/(c1-d1)
# y-c2=q*(x-c1)
# q*x - y = q*c1 - c2
if(p==q) return(NA)
else{
# M=matrix(c(p,q,-1,-1),nrow=2)
# v=c(p*a1-a2, q*c1-c2)
# s=solve(M,v)
# s[1]+1i*s[2]
x= ((p*a1 - a2) - (q*c1 - c2))/ (p-q)
y= p*x - ( p*a1 - a2)
x + 1iy
}
}
ウォーキングで10kmの坂道を減速し続けながら登る。
走行距離に比例して速度は減速する。
時速6km/hで登り始め、時速4km/hで頂上に到着したものとする。
このとき、坂道を登るのに要した時間はいくらか？
>>340 v0=6 ; v1=4 ; s1=10
v(t)=ds(t)/dt=as(t)+v0
s(t)= Ce^(at) - v0/a
v(t)=aC*e^(at)
t0=0
v(t0)=aC=v0 ∴ C=v0/a
v(t1)=aC*e^(at1)=v1 ∴ e^(at1)=v1/(aC)=v1/v0
s(t1)=Ce^(at1)-v0/a=s1 ∴ (v0/a)*(v1/v0)-v0/a=s1
a = (v1 - v0)/s1
C = v0/a
= v0*s1/(v1-v0)
# 距離を与えて所要時間を返す
t <- function(s1,v0=6,v1=4){ # s1:距離 v0:初速 v1:終速
a = (v1 - v0)/s1
C= v0*s1/(v1-v0)
t = log((a*s1 + v0)/(a*C))/a
return(t)
}
t(10)
t(20)
curve(t(x),0,50,bty='l',xlab='走行距離',ylab='所要時間')
# 時間を与えて走行距離を返す
s <- function(t1,s1=10,v0=6,v1=4){
a = (v1 - v0)/s1
C = v0*s1/(v1-v0)
s = C*exp(a*t1) - v0/a
return(s)
}
s(1)
s(2.027326)
s(5)
curve(s(x),0,30,xlab='走行時間',ylab='到達距離',bty='l')
>>342 これ、ｔの方は間違えているので撤回します。
どんどん減速するから、そんなに長距離を進める筈がないｗ
ウォーキングで10kmの坂道を減速し続けながら登る。
走行距離に比例して速度は減速する。
時速6km/hで登り始め、時速4km/hで頂上に到着したものとする。
このとき、坂道を登るのに要した時間はいくらか？
v(t)=ds(t)/dt=as(t)+v0
s(t)= Ce^(at) - v0/a
v(t)=aC*e^(at)
t0=0
v(t0)=aC=v0 ∴ C=v0/a
v(t1)=aC*e^(at1)=v1 ∴ e^(at1)=v1/(aC)=v1/v0
s(t1)=Ce^(at1)-v0/a=s1 ∴ (v0/a)*(v1/v0)-v0/a=s1
a = (v1 - v0)/s1
C = v0/a
= v0*s1/(v1-v0)
# 距離を与えて所要時間を返す
t <- function(s,s1=10,v0=6,v1=4){ # s1:距離 v0:初速 v1:終速
a = (v1 - v0)/s1
C= v0*s1/(v1-v0)
t = ifelse(s>-v0/a,NA,log((a*s + v0)/(a*C))/a)
return(t)
}
t(10)
t(20)
t(25)
curve(t(x),0,30,bty='l',xlab='走行距離',ylab='所要時間')
# 時間を与えて走行距離を返す
s <- function(t1,s1=10,v0=6,v1=4){
a = (v1 - v0)/s1
C = v0*s1/(v1-v0)
S = C*exp(a*t1) - v0/a
return(S)
}
s(1)
s(2.027326)
s(24)
curve(s(x),0,30,xlab='走行時間',ylab='到達距離',bty='l')
# 距離を与えて所要時間を返す
> t(10)
[1] 2.027326
> t(20)
[1] 5.493061
> t(25)
[1] 8.958797
> # 時間を与えて走行距離を返す
>>405 > s(1)
[1] 5.438077
> s(2.027326)
[1] 10
> s(24)
[1] 29.75311
スレ主ウリュウヒロユキいうのか
ふーん
フフフフフ
P : (p1,p2)
Q : (q1,q2)
Q2 : (r1,r2)
角Q2-P-Q = atan((r2-p2)/(r1-p1)) - atan((q2-p2)/(q1-p1)
atanはtanの逆関数、x=tan(θ) θ=atan(x)
>>347 違うけど。
俺、医科歯科卒。
あんたは？
# 交点の座標を返す
intsect <- function(a,b,c,d){
a1=Re(a) ; a2=Im(a)
b1=Re(b) ; b2=Im(b)
p=(a2-b2)/(a1-b1)
# y-a2=p*(x-a1)
# p*x - y = p*a1 - a2
c1=Re(c) ; c2=Im(c)
d1=Re(d) ; d2=Im(d)
q=(c2-d2)/(c1-d1)
# y-c2=q*(x-c1)
# q*x - y = q*c1 - c2
if(p==q) return(NA)
else{
# M=matrix(c(p,q,-1,-1),nrow=2)
# v=c(p*a1-a2, q*c1-c2)
# s=solve(M,v)
# s[1]+1i*s[2]
x= ((p*a1 - a2) - (q*c1 - c2))/ (p-q)
y= p*x - ( p*a1 - a2)
x + 1i*y
}
}
plot(NULL,xlim=c(-10,30),ylim=c(0,25),xlab='',ylab='',type='n',bty='l',asp=1)
A=0;B=20;C=20+20i;D=20i
pt(A,'A') ; pt(B,'B'); pt(C,'C') ; pt(D,'D')
seg(A,B,col=8) ; seg(B,C,col=8) ; seg(C,D,col=8) ; seg(D,A,col=8)
E=20+3i ; F=30+3i ; G=30+13i ; H=20+13i
pt(E,'E') ; pt(F,'F') ; pt(G,'G') ; pt(H,'H')
seg(E,F,col=8) ; seg(F,G,col=8) ; seg(G,H,col=8)
seg(D,B,col=8) ; seg(A,C,col=8) ; seg(F,H,col=8) ; seg(E,G,col=8)
pt(P,'P')
pt(Q,'Q',cex=1.2)
P
Q
seg(P,Q,col=2)
cir(Re(P),Im(P),abs(P-Q),lty=3)
Q2=abs(Q-P)*(cos(Arg(Q-P)+pi/6)+1i*sin(Arg(Q-P)+pi/6))+P
pt(Q2,'Q2',cex=1.2)
seg(P,Q2,col=2)
"
△ABCの外部に3つの正三角形△PBC,△QCA,△RABをとる（いずれの三角形も△ABC内部の領域と共通部分を持たない）。
△ABCの形状が色々変化するとき、以下のrの取りうる値の範囲を求めよ。
r = {max(AP,BQ,CR)}/(AB+BC+CA)
source('toolmini.R')
# ある点P（複素点)が三角形ABCの内部にあるか？
opc <- function(a,b){ # outer product on complex plane
Re(a)*Im(b)-Im(a)*Re(b)
}
in3 <- function(P,A,B,C){ # is P inside triangle ABC?
sum(opc(B-A,P-A)>0,opc(C-B,P-B)>0,opc(P-A,C-A)>0)%%3==0
# 右ねじ外積の方向がZ軸で全て正か全て負かで三角形の内部と確認
}
# 線分PQの座標から正三角形PQR,PQSを作るR,Sの座標を返す
seg2tri <- function(P=runif(1)+1i*runif(1),Q=runif(1)+1i*runif(1),print=FALSE,...){
PQ=Q-P
R=abs(PQ)*(cos(Arg(PQ)+pi/3)+1i*sin(Arg(PQ)+pi/3))+P
S=abs(PQ)*(cos(Arg(PQ)-pi/3)+1i*sin(Arg(PQ)-pi/3))+P
if(print) { seg(P,R,...) ; seg(Q,R,...) ; seg(P,S,...) ; seg(Q,S,...)}
return(c(R,S))
}
# demo seg2tri(print=TRUE,col=8)
# △PBC,△QCA,△RAB
par(lwd=2)
art <- function(print=FALSE) { # adjacent regular triangle
plot(0,type='n',axes=F,ann=F,xlim=c(-1.5,1.5),ylim=c(-1,1.5),asp=1)
A= -0.5 ; B= 0.5
x=runif(1) ; y=runif(1)
C=x+1i*y
if(print){pt(A,'A');pt(B,'B');pt(C,'C') ; seg(A,B);seg(A,C);seg(B,C)}
r=seg2tri(A,B,print=FALSE)
r12=c(opc(B-A,r[1]-A),opc(B-A,r[2]-A))
R=r[ifelse(opc(B-A,C)>0,which.min(r12),which.max(r12))]
if(print) {pt(R,'R') ; seg(A,R,col=2) ; seg(B,R,col=2)}
p=seg2tri(B,C,print=FALSE)
p12=c(opc(C-B,p[1]-B),opc(C-B,p[2]-B))
P=p[ifelse(opc(C-B,A)>0,which.min(p12),which.max(p12))]
if(print) {pt(P,'P') ; seg(B,P,col=2) ; seg(C,P,col=2)}
q=seg2tri(C,A,print=FALSE)
q12=c(opc(A-C,q[1]-C),opc(A-C,q[2]-C))
Q=q[ifelse(opc(A-C,B)>0,which.min(q12),which.max(q12))]
if(print) {pt(Q,'Q') ; seg(A,Q,col=2) ; seg(C,Q,col=2)}
# r = {max(AP,BQ,CR)}/(AB+BC+CA)
r=max(abs(A-P),abs(B-Q),abs(C-R))/(abs(A-B)+abs(B-C)+abs(C-A))
if(print) legend('bottom',bty='n',legend=paste('r =',round(r,2)))
return(r)
}
art(print=TRUE)
layout(matrix(1:9,3))
replicate(9,art(T))
layout(1)
par(lwd=1)
re=replicate(1e4,art(F))
range(re)
> re=replicate(1e4,art(F))
> range(re)
[1] 0.4340035 0.5773468
>>352 動作確認してみた。
>>356 これをいつまで経っても答がだせない、アホだらけだよ。
前々スレからのド底辺シリツ医への宿題
若い女性研修医（嘘つきかどうかは不明）から
「あなたのいうことが正しければ手コキかフェラをしてあげる、そうでなければセンズリを命じる」と言われた。
フェラをしてもらうには何と言えばいいか？
>>349 フフ、私立だがバッチリ医学科
出てるぞ
歯科は医者ではなーい！
ハハハハ
>>359 >358に答えてみ！
できなきゃ裏口認定
# draw text y at x and perpendicular line
ptl <- function(x,y=NULL,...){
if(is.complex(x)) {a=Re(x) ; b=Im(x)}
else{a=x[1] ; b=x[2]}
text(a,b, ifelse(is.null(y),'+',y), ...)
segments(a,0,a,b,lty=3) ; segments(0,b,a,b,lty=3)
}
rm(list=ls())
source('toolmini.R')
θ=pi/3
α=0.1303291
eclip <- function(x,z){
sqrt(x^2+z^2)/tan(θ) - (tan(α)*(x-sin(θ))+cos(θ))
}
eclipse=Vectorize(eclip)
x=z=seq(-sin(θ),sin(θ),0.01)
y=outer(x,z,eclipse)
contour(x,z,y,levels=0,drawlabels = F,xlim=c(-1,1),asp=1)
我々底辺私立卒医こそ大正義
貧乏国立卒医と違って上級国民だよｗ
でも底辺私立卒医と言っても
早慶非医学部より難関だけどなｗ
ワイングラスの形状が円錐面とする。
グラス底での角度２θは１２０°する。（θ＝６０°)
これを傾けて満杯のワインを半分にするには何度傾ければよいか？
cos(θ+α)/cos(θ-α)= 4^(-1/3)
>>363 早稲田の理工と川崎医って川崎医の方が難しいの？
>>364 α = acos(sqrt(sin^2(θ) - cos^2(θ) + 2^(1/3) + 1)/sqrt(2))
>>365 早稲田の理工なら>364を解けるが川崎だと無理だろう。
あんたにも無理だろうから>358でも答えてみ！
solve cos(θ+x)=p^(2/3)*cos(θ-x) for x where θ=pi/3 and p=0.5 and 0<x<pi/2
円錐の展開図を描いて、その側面部に円を描きます。この展開図を組み立てて円錐としたとき、側面の円はどのような図形になるのでしょうか。
>>372>>971
グラフ化してみました。割と大変だったな。
プログラムができたから
蚊取り線香を円錐側面に載せてみました。
graph <- function(p=0.5){ # θ:cone angle, α:tilt, P:volume proportion
θ=seq(0,pi/2,0.01)
α=seq(0,pi/2,0.01)
fn <- function(θ,α,P=p) cos(θ+α)- P^(2/3)*cos(θ-α)
fn=Vectorize(fn)
z=outer(θ,α,fn)
contour(θ,α,z,levels = 0, drawlabels = F,xlab='θ(rad)',ylab='α(rad)',asp=1,bty='l')
}
graph()
tilt <- function(th,p=0.5){ # p=0.5 and 0< θ < pi/2
fn <- function(theta=th,x,P=p) cos(theta+x) - P^(2/3)*cos(theta-x)
fn=Vectorize(fn)
uniroot(function(x) fn(th,x,p),c(0,pi/6))$root
}
> tilt(pi/3)*180/pi
[1] 7.466948
約7.5°だな。
Schema <- function(){
plot(NULL,type='n',xlim=c(-1,1),ylim=c(0,1.5),asp=1,ann=F)
abline(h=0,v=0,col=8,lty=3)
α=25*pi/180
pt(-0.025+0.125i,'α')
th=pi/2-α
seg(0,-cos(th)+1i*sin(th),col=8,lty=3)
seg(-cos(th)+1i*sin(th),0,col=8,lty=3)
a=2*pi*cos(th) # 2*pi*sin(θ/2)
seg(0,cos(pi/2-a/2)+1i*sin(pi/2-a/2))
seg(0,cos(pi/2+a/2)+1i*sin(pi/2+a/2))
curve(sqrt(1-x^2),cos(pi/2+a/2),cos(pi/2-a/2),add=T)
# 2β=2πr
# r=sin(α)=β/π
# ∴ β=π*sin(α)
β=pi*sin(α)
α=asin(β/pi)
r=β/pi
seg(-r+1i*cos(α),1i*cos(α),lty=3,col=8)
curve(sqrt(0.25^2-x^2),-0.25/tan(pi/2-β),0,col=8,lty=2,add=T)
pt(-0.2+0.2i,'β')
pt(-0.2+0.925i,'r')
p=0.7 ; q=sqrt(1-p^2)
A=p+1i*q ; pt(A+0.1,'A(p,q)')
seg(0,A,col=8)
# z=2*r=2*β/pi
# y=cos(α)=cos(asin(β/pi))
# x=cos(-pi/2+β/r)=sin(β/r)
cir(0,1+r,r,col=4) ; pt(c(0,1+r))
pt(0.05+0.125i,'θ')
θ=atan(p/q)
(xA=r*cos(-pi/2+θ/r))
r*sin(θ/r)
(β/pi)*sin(pi*θ/β)
(β/pi)*sin(pi*atan(p/q)/β)
Adash=xA+1i*(sqrt(r^2-xA^2)+1+r)
pt(Adash,'A\'') ; pt(0.2+1.5i,'r')
seg(Adash,(1+r)*1i,lty=3,col=8)
(yA=sqrt(p^2+q^2)*cos(θ))
sqrt(p^2+q^2)*cos(atan(p/q))
(zA=sqrt(p^2+q^2)*r*2)
}
Schema()
r’=sqrt(p^2+q^2) β/pi
γ=θpi/β
x=r'sin(γ)
y=√()cos(β)
z= √()+r'-r'cos(θpi/β)
β=pi*sin(α)
α=asin(β/pi)
r=β/pi
>>382 A(p,q):展開図上の座標
tan(θ)=q/p , θ=atan(q/p)
r':Aの円錐上で点A’を通る円Cの半径
γ:x=0面と、A'と円Cの中心を結ぶ線とAの角度
cone <- function(p,q,α){
θ=atan(p/q)
β=pi*sin(α)
γ=pi*θ/β
PQ=sqrt(p^2+q^2)
rdash=PQ*β/pi
x=rdash*sin(γ)
y=PQ*cos(β)
z=PQ+rdash-rdash*cos(γ)
c(x,y,z)
}
oncone <- function(p,q,α=pi/6){ # (p,q) 展開図上の座標、頂点の角度=２α
PQ=sqrt(p^2+q^2)
β=pi*sin(α)
θ=atan(p/q)
rdash=PQ*β/pi
γ=PQ*θ/rdash
x=rdash*sin(γ)
y=PQ/(tan(α)*sqrt(1+tan(α)^-2))
z=rdash*(1-cos(γ))
c(x=x,y=y,z=z)
}
onCone=Vectorize(oncone)
onCone(1:3,4:6)
library(rgl)
p0=0 ; q0=0.5 ; r=0.3
theta=seq(-pi,pi,0.01)
p=r*cos(theta)+p0
q=r*sin(theta)+q0
points(p,q,asp=1,col=2)
re=onCone(p,q)
x=re['x',] ;y=re['y',];z=re['z',]
rgl::plot3d(x,y,z,col='brown')
library(scatterplot3d)
scatterplot3d(x, y, z, highlight.3d=TRUE, col.axis="blue",
col.grid="lightblue", main="メガホンに輪ゴム", pch=20)
>>378 頭が悪いのを金で補うのが普通だってｗ
さては売らシリツ医だな。
numlockキーをbackspaceキーに変更するレジストリ（要再起動）
Windows Registry Editor Version 5.00
[HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Control\Keyboard Layout]
"Scancode Map"=hex:00,00,00,00,00,00,00,00,02,00,00,00,0e,00,45,00,00,00,00,00
母線の長さが１、円錐角（母線と軸のなす角）がθの円錐側面の展開図を頂点を原点にｙ軸に対称に置く。円錐底面の円は考えない。
展開図上の点Aの座標を(p,q)とすると展開図を円錐化したときのAの三次元座標をp,q,θで表わせ。
( x, y ) → √(x*x+y*y) * ( sinΘ*cos(atan2(y, x) /sinΘ), r*sinΘ*sin(atan2(y, x) /sinΘ), cosΘ )
f <- function(x){
m=sum(x)
sub <- function(n){
if(n==1) return(1)
else{
return(n*Recall(n-1))
}
}
sub(m)
}
f(c(1,2,3))
>>392 # x=sqrt(p^2+q^2)*sin(α)*sin(atan(p/q)/sin(α))
# y=sqrt(p^2+q^2)/(tan(α)*sqrt(1+tan(α)^-2))
# z=sqrt(p^2+q^2)*sin(α)*(1-cos(atan(p/q)/sin(α)))
# 円錐角から展開図を表示
opened <- function(α=25*pi/180,R=1){
plot(NULL,type='n',xlim=c(-R,R),ylim=c(-R,R),asp=1,ann=F,axes=F)
abline(h=0,v=0,col=8,lty=3)
β=pi*sin(α)
seg(0,-R*sin(α)+R*1i*cos(α))
seg(0, R*sin(α)+R*1i*cos(α))
seg(-R*sin(α)+R*1i*cos(α),R*sin(α)+R*1i*cos(α))
seg(0,-R*sin(β)+R*1i*cos(β),lty=2)
seg(0, R*sin(β)+R*1i*cos(β),lty=2)
pt(R*0.2*(-sin(α/2)+1i*cos(α/2)),'α')
alpha=seq(pi/2,pi/2+α,0.01)
lines(0.2*R*cos(alpha),0.2*R*sin(alpha),col=8)
pt(R*0.3*(-sin(β/2)+1i*cos(β/2)),'β')
beta=seq(pi/2,pi/2+β,0.01)
lines(0.3*R*cos(beta),0.3*R*sin(beta),col=8)
Beta=seq(pi/2-β,pi/2+β,0.01)
lines(R*cos(Beta),R*sin(Beta),lty=2)
}
opened(40*pi/180)
底辺リシツ医師は問題外だが
自治医大卒の尾身をなんとかみんなでどうにかしてくれ～
ＰＣＲ増えないね
f <- function(s,t) s^2 + 4*s*t - 2*t^2 - 3*s + 2
s=t=seq(0,1,0.01)
z=outer(s,t,f)
contour(s,t,z)
inside <-function(x,y,z){
(x>=0 & z^2+y^2 < 1/2*( sqrt(4*x + 1) + 2*x + 1 - 2*x^2))|
(x<0 & (z^2+y^2 < 1/2*( sqrt(4*x + 1) + 2*x + 1 - 2*x^2)) &
(z^2+y^2 > 1/2*(-sqrt(4*x + 1) + 2*x + 1 - 2*x^2)))
}
N=1e4
x=runif(N,-0.25,2)
y=runif(N,-1.3,1.3)
z=runif(N,-1.3,1.3)
v=diff(range(x))*diff(range(y))*diff(range(z))
w=NULL
counter=0
for(i in 1:N){
if(inside(x[i],y[i],z[i])){
w=rbind(w,c(x[i],y[i],z[i]))
counter=counter+1
}
}
counter/N*v
rgl::plot3d(w[,1],w[,2],w[,3],col='red',asp=1)
rgl::plot3d(w[,1],w[,2],w[,3],col=sample(c('black','red')),asp=1)
rgl::plot3d(w[,1],w[,2],w[,3],col=sample(colours()),asp=1)
アベがベトナム移民を連れてきた
x=√(p^2+q^2)sin(α)
y=rdash/tan(α)=√(p^2+q^2)sin(α)tan(α)
gamma=atan(p/q)/sin(alpha)
√(p^2+q^2)sin(alpha)(1-cos(atan(p/q)/sin(alpha))
z=√(p^2+q^2)sin(α)(1-cos(atan(p/q)/sin(α))
rm(list=ls())
source('toolmini.R')
# 円錐角から展開図を表示
opened <- function(α=40*pi/180,R=1){
plot(NULL,type='n',xlim=c(-R,R),ylim=c(-R,R),asp=1,ann=F,axes=T)
abline(h=0,v=0,col=8,lty=3)
β=pi*sin(α)
seg(0,-R*sin(α)+R*1i*cos(α))
seg(0, R*sin(α)+R*1i*cos(α))
# seg(-R*sin(α)+R*1i*cos(α),R*sin(α)+R*1i*cos(α))
seg(0,-R*sin(β)+R*1i*cos(β),lty=2)
seg(0, R*sin(β)+R*1i*cos(β),lty=2)
pt(R*0.2*(-sin(α/2)+1i*cos(α/2)),'α') ; pt(R*0.2*(sin(α/2)+1i*cos(α/2)),'α')
alpha=seq(pi/2-α,pi/2,0.01)
lines(0.18*R*cos(alpha),0.18*R*sin(alpha),col=8)
alpha=seq(pi/2,pi/2+α,0.01)
lines(0.20*R*cos(alpha),0.20*R*sin(alpha),col=8)
pt(R*0.3*(-sin(β/2)+1i*cos(β/2)),'β') ; pt(R*0.3*(sin(β/2)+1i*cos(β/2)),'β')
beta=seq(pi/2,pi/2+β,0.01)
lines(0.3*R*cos(beta),0.3*R*sin(beta),col=8)
beta=seq(pi/2-β,pi/2,0.01)
lines(0.28*R*cos(beta),0.28*R*sin(beta),col=8)
Beta=seq(pi/2-β,pi/2+β,0.01)
lines(R*cos(Beta),R*sin(Beta),lty=2)
pt(-0.025i*R,'O')
p=0.7*R;q=0.3*R
A=p+1i*q ; pt(A,'A(p,q)')
seg(A,0,col=8)
OA=abs(A-0)
(θ=atan(q/p)) ; Arg(A)
pt(0.1*OA*cos(θ/2)+1i*0.1*OA*sin(θ/2),'θ')
th=seq(0,θ,0.01)
lines(0.2*OA*cos(th),0.2*OA*sin(th),col=8)
th=seq(pi/2-β,pi/2+β,0.01)
lines(OA*cos(th),OA*sin(th),col=8)
B=OA*1i ; pt(B,'B',cex=1.2)
C=OA*cos(pi/2-β)+1i*OA*sin(pi/2-β) ; pt(C,'C')
(rdash=OA*β/pi) # ⌒BC＝πｒ' where β = pi*sin(α), then rdash=OA*sin(α)
cir(0,OA+rdash,rdash,col=8)
D=1i*(OA+rdash) ; pt(D,'D')
th=seq(θ,pi/2,0.1)
lines(OA*cos(th),OA*sin(th),col=2,lwd=2)
# arc(BA)＝arc(BE) OA*(pi/2-θ)=rdash*δ
δ=OA*(pi/2-θ)/rdash # OA*(pi/2-θ)/OA*sin(α) = (pi/2-θ)/sin(α)
th=seq(-pi/2,-pi/2+δ,0.01)
lines(rdash*cos(th),rdash*sin(th)+(OA+rdash),lwd=2,col=4)
lines(0.2*rdash*cos(th),0.2*rdash*sin(th)+(OA+rdash),col=8)
E=rdash*sin(δ)+1i*(rdash*(1-cos(δ))+OA) ; pt(E,'E')
seg(D,E,col=8)
pt((D+E)/2,'r\'')
pt(0.2*rdash*cos(-pi/2+δ/2)+1i*0.2*rdash*sin(-pi/2+δ/2)+D,'δ')
}
opened(40*pi/180)
oncone <- function(p,q,α=40*pi/180){ # (p,q) 展開図上の座標、頂点の角度=２α
OA=sqrt(p^2+q^2)
θ=Arg(p+1i*q)
β=pi*sin(α) # π*r=R*β ; r=R*sin(α)
rdash=OA*sin(α) # r'== OA*β/π, r'*π == OA*β : hemi-circle==arc(B-c)
δ=(pi/2-θ)/sin(α) # r'*δ == OA*(π/2-θ) ; δ == OA*(π/2-θ)/r'
x=rdash*sin(δ) # Re(E)
y=rdash/tan(α) # tan(α)=r'/y
z=rdash-rdash*cos(δ) # IM(E-B) ; rdash+rdash(cos(π-δ))
c(x=x,y=y,z=z)
}
onCone=Vectorize(oncone)
oncone <- function(p,q,α=40*pi/180){ # (p,q) 展開図上の座標、頂点の角度=２α
OA=sqrt(p^2+q^2)
θ=Arg(p+1i*q)
β=pi*sin(α) # π*r=R*β ; r=R*sin(α)
rdash=OA*sin(α) # r'== OA*β/π, r'*π == OA*β : hemi-circle==arc(B-c)
δ=(pi/2-θ)/sin(α) # r'*δ == OA*(π/2-θ) ; δ == OA*(π/2-θ)/r'
x=rdash*sin(δ) # Re(E)
y=rdash/tan(α) # tan(α)=r'/y
z=rdash-rdash*cos(δ) # IM(E-B) ; rdash+rdash(cos(π-δ))
c(x=x,y=y,z=z)
}
ド底辺シリツ医には解けないであろう問題。
プログラムして２０度以外でも答がでるようにしてみた。
intsect <- function(a,b,c,d){
a1=Re(a) ; a2=Im(a)
b1=Re(b) ; b2=Im(b)
p=(a2-b2)/(a1-b1)
c1=Re(c) ; c2=Im(c)
d1=Re(d) ; d2=Im(d)
q=(c2-d2)/(c1-d1)
if(p==q) return(NA)
else{
x= ((p*a1 - a2) - (q*c1 - c2))/ (p-q)
y= p*x - ( p*a1 - a2)
x + 1i*y
}
}
foo <- function(N20=20){
plot(NULL,type='n',xlim=c(0,2),ylim=c(0,2),asp=1,ann=F)
u=pi/180
A=cos(N20*u)+1i*sin(N20*u) ; pt(A,'A')
seg(0,A)
B=cos(2*N20*u)+1i*sin(2*N20*u) ; pt(B,'B')
seg(0,B)
seg(A,B)
abline(h=0,col=8)
a=Arg(A-B)/u+N20
f <- function(x) tan(a*u)*(x-Re(B))+Im(B)
curve(f(x),add=T,col=8)
C=intsect(0i,1+0i,B,1i*f(0)) ; pt(C,'C')
seg(C,A)
(Arg(A-C)-Arg(B-C))/u
}
foo=Vectorize(foo)
x=foo(1:35)
data.frame(angle=1:35,x=x)
>>413 
atanだと返り値が-pi/2,pi/2なのでうまくいかなかった。
偏角を返すArgにしてようやくデバッグできた。
x = (a^2 - b^2 + c^2)/(2 a),
y = sqrt(c^2 - (a^2 - b^2 + c^2)^2/(4 a^2))
x^2+y^2=c^2, (x-a)^2+y^2=b^2
売国してんのは他ならぬ自称保守層（笑）だからな
IR汚職で中国から献金貰って逮捕されたのは靖国にも参拝する自民議員と維新だろ
竹島の日削除したのも自民党
北方領土献上したのも自民党
尖閣諸島で何もしないのも自民党
# draw arc A:center theta:angle
Arc <- function(A,B,theta,...){
th0=Arg(B-A)
th1=th0+theta
th=seq(th0,th1,0.01)
r=abs(B-A)
z=r*cos(th)+1i*r*sin(th)+A
lines(z,...)
}
source('toolmini.R')
plot(NULL,type='n',xlim=c(0,2),ylim=c(0,2),asp=1,ann=F)
p=ngon(7,col=0,digit=F,axes=F)
r=abs(p[7]-p[3])
th=BAC(p[4],p[7],p[3])[1]
for(i in 1:4) Arc(p[i],p[i+3],th,lwd=2)
for(i in 5:7) Arc(p[i],p[(i+3)%%7],th,lwd=2)
50ペンス硬貨の輪郭
HK
2:18 / 2:34
Prince Rupert’s cube live demonstration
ダウンロード＆関連動画＞＞
@YouTube これが医師国家試験問題とは! 単なる比例計算。中学入試より易しい。
中学入試
Xの角度は？（立体ではなくて平面図）
ド底辺シリツ医のこれが現実
１次方程式もできないド底辺シリツ医大卒の記録
実際、算数の掛け算すら怪しいシリツ医がこういう事故を起こしている。
カージオイドの面積だけなら、極形式のままでモンテカルロで計算できる。
# r=func(θ)を描く
Draw <- function(func,th=seq(-pi,pi,length=500),...){
r=func(th)
x=r*cos(th)
y=r*sin(th)
plot(x,y,bty='l',type='l', ann=F,lwd=2,...)
invisible(list(x=x,y=y))
}
Draw(function(th) 1 + cos(th),asp=1,col='red')
abline(h=0,v=0,lty=3)
N=1e8
x=runif(N,-0.25,2)
y=runif(N,-1.3,1.3)
s=diff(range(x))*diff(range(y))
r=sqrt(x^2+y^2)
th=atan2(y,x) # Arg(x+1i*y)
s*mean(r<1+cos(th)) ; 3/2*pi
N=9
str='floor(x)+'
for (i in 2:(N-1)) {
str=c(str,paste0('floor(',i,'*x)+',collapse=''))
}
str=c(str,paste0('floor(',N,'*x)'))
str=paste0(str,collapse='')
str
f <- function(n){
m=sum(1:N)-1
x=n/m
eval(str2lang(str)) - m*x
}
ジュースディスペンサー
例
に１００％天然果汁が１０L入っていて常に撹拌されている。
すなわち、濃度はいつも均一とする設定。
コックにトラブルがあって１分間に１０ｍLずつ漏れている。
それを補うために１分間に１０ｍLの天然水を補っているとする。
５０％天然果汁のジュースになるのは何分後か？
(1-0.001*t)^n=0.5
lim[t→0] t*log(0.5)/log(1-0.001t)
補充が５mLで１分毎に間欠的行われるとすると
v(0)=10000
v(1)=10000-10+5
v(t)=10000-5*t
c(0)=1
c(1)=9990/9995=c(0)*(v(0)-10)/v(1)
c(2)=c(1)*(v(1)-10)/v(2)
c(t+1)=c(t)*(v(t)-10)/v(t+1)
=c(t)*(10000-5*t-10)/(10000-5(t+1))
V(0)=10000
V(1)=10000-10+5
V(t)=10000-5*t
C(0)=1
C(1)=9990/9995=C(0)*(V(0)-10)/V(1)
C(2)=C(1)*(V(1)-10)/V(2)
C(t+1)=C(t)*(V(t)-10)/V(t+1)
C=numeric()
C[1]=9990/9995
for(t in 1:1000){
C[t+1]=C[t]*(10000-5*t-10)/(10000-5*(t+1))
}
C
V(0)=10000
V(1)=10000-10+5
V(t)=10000-5*t
C(0)=1
C(1)=9990/9995=C(0)*(V(0)-10)/V(1)
C(2)=C(1)*(V(1)-10)/V(2)
C(t+1)=C(t)*(V(t)-10)/V(t+1)
C=numeric()
C[1]=9990/9995
for(t in 1:1000){
C[t+1]=C[t]*(10000-5*t-10)/(10000-5*(t+1))
}
C
V(0)=10000
V(1)=10000-10+5
V(t)=10000-5*t
C(0)=1
C(1)=9990/9995=C(0)*(V(0)-10)/V(1)
C(2)=C(1)*(V(1)-10)/V(2)
C(t+1)=C(t)*(V(t)-10)/V(t+1)
C=numeric()
C[1]=9990/9995
for(t in 1:1000){
C[t+1]=C[t]*(10000-5*t-10)/(10000-5*(t+1))
}
C
これみてこんな問題を思いついた。
カージオイドr=1+cosθ
で囲まれた面をｙ軸の周りに回転させてできる立体の体積をVとする。直線x=aを軸に回転させてできる立体の体積がV/2であるようなaの値はいくらか？
D(expression((1+cos(θ))*sin(θ)),'θ')
f60_90 <- function(th) pi*((1+cos(th))*cos(th))^2*(-sin(th)^2+cos(th)^2+cos(th))
(vb=integrate(f60_90,0,pi/3)$value)
(vg=integrate(f60_90,pi/2,pi/3)$value)
(vb - vg)*2
> (vb - vg)*2
[1] 24.90338
１分毎に間欠的に5mLの水を補充するモデルで考えた。
V(t):t分後のジュースの総量
C(t):をt分後の濃度
V(0)=10000
V(1)=10000-10+5
V(t)=10000-5*t
C(0)=1
C(1)=9990/9995=C(0)*(V(0)-10)/V(1)
C(2)=C(1)*(V(1)-10)/V(2)
C(t+1)=C(t)*(V(t)-10)/V(t+1)
１分毎に間欠的に5mLの水を補充するモデルで考えた。
V(t):t分後のジュースの総量
C(t):をt分後の濃度
V(0)=10000
V(1)=10000-10+5
V(t)=10000-5*t
C(0)=1
C(1)=9990/9995=C(0)*(V(0)-10)/V(1)
C(2)=C(1)*(V(1)-10)/V(2)
C(t+1)=C(t)*(V(t)-10)/V(t+1) = C(t)*(10000-5*t-10)/(10000-5*(t+1))
ヤラセの質疑応答の原稿を晒してしまっている。
ジュースディスペンサー
例
に１００％天然果汁が１０L入っていて常に撹拌されている。
すなわち、濃度はいつも均一。
コックにトラブルがあって１分間に１０ｍLずつジュースが漏れている。
それを補うために１分毎に間欠的に５ｍLの天然水を補っているとする。
５０％天然果汁のジュースになるのは何分後か？そのときのジュースの総量は？
ジュースディスペンサー
例
に１００％天然果汁が１０L入っていて常に撹拌されている。
すなわち、濃度はいつも均一。
コックにトラブルがあって１分間に１０ｍLずつジュースが漏れている。
それを補うために１分毎に間欠的に５ｍLの天然水を補っているとする。
５０％天然果汁のジュースになるのは何分後か？そのときのジュースの総量は？
とりあえず、作図（n=3）のとき。
#Recall二題
f <- function(...){
x=c(...)
if(length(x) == 0) return(1)
abs(x[1]) * Recall(x[-1])
}
f(1:100)
f <- function(...){
v=c(...)
n=length(v)
sub<-function(n){
if(n==0) return(1)
else abs(v[n])*Recall(n-1)
}
sub(n)
}
f(1:100)
世界の平均年収(円)
1995年→2005年→2015年
アメリカ:460→546→658
ドイツ:251→522→587
ポーランド:53→137→312
フランス:226→533→568
韓国:77→219→385
日本:445→440→415
世界中で日本だけ25年前から下がり続け、欧州諸国にはとっくに追い抜かされ差を広げられ続け、
韓国にすら追いつかれている(所得中央値は韓国以下)
この25年間以上、世界中で貧しくなったのは、【日本だけ】
小泉・竹中が築き上げた非正規雇用天国の日本は、貧困層激増し、これからも未婚率&少子化は大促進する
「高収入」が「1000万円以上」とされてたのはバブルの頃既に。
それから40年たっても未だに高収入が1000万円以上。
一方、諸外国では順調に給料をのばしたので、日本人の給料が
どんどん安い側に落ちてきている。
典型的なのが自動車で、昔は600万円程度だったクルマが今は
千何百万円とかになってるが日本人の給料はほとんど変わらないので
もの凄い高嶺の花になってしまった。昔は200万円程度だった日本車が
今は３百数十万くらいで「高くて買えない」になってる。
熊に襲われて死ぬのは年間1人か2人だから、熊の対策なんていらないな。
暴力団の抗争に巻き込まれて死ぬ人も数人出ればいいとこだし、特に問題ない。
地下鉄サリン事件での死者は14人くらいだから。
安心して経済活動を行ってくれればいい
ミンス時代と違って幸せで穏やかで平和な日々が続いて心からウレシイ
じっさい、安倍政権になってから
めだって大きな災害は減り続けて最近は、疫病の流行もほぼゼロだよね
なんども来てた台風はなかなか来ないし水害も地震もミンス時代と違ってそんなに起きてない
あの東日本大震災は、自民党を裏切った国民に対して天が下した罰だったんだよ
ベタだけど「安倍総理のもとコロナに立ち向かう嬉しさよ、日本に生まれて良かった！」
ｓｑｒｔ（１＋ｓｑｒｔ（２＋ｓｑｒｔ（３＋ｓｑｒｔ（４＋．．．
↑これ収束しそうなんですがどういう値か求める方法教えてくれませんか？
といおう投稿があったので数式を書くプログラムを書いてみた。
ｓｑｒｔｓｅｑ ＜－ ｆｕｎｃｔｉｏｎ（ｎ）｛ ＃ ３ －＞ ＂ｓｑｒｔ（１＋ｓｑｒｔ（２＋ｓｑｒｔ（３）））＂
＇％＆％＇ ＜－ ｆｕｎｃｔｉｏｎ（ｘ，ｙ） ｐａｓｔｅ０（ｘ，ｙ）
ｓ ＝ ｖｅｃｔｏｒ（＇ｌｉｓｔ＇）
ｓ［［１］］ ＝ ＂ｓｑｒｔ（１）＂
ｉｆ（ｎ＝＝１） ｒｅｔｕｒｎ（ｓ［［１］］）
ｆｏｒ（ｉ ｉｎ ２：ｎ）｛
ｎｃ ＝ ｎｃｈａｒ（ｓ［［ｉ－１］］）
ｅｎｄ＿ｓ＝ｐａｓｔｅ０（ｒｅｐ（＇）＇，ｉ），ｃｏｌｌａｐｓｅ＝＇＇）
ｓ［［ｉ］］＝ｓｕｂｓｔｒ（ｓ［［ｉ－１］］，１，ｎｃ－ｉ＋１） ％＆％ ＂＋ｓｑｒｔ（＂ ％＆％ ｉ ％＆％ ｅｎｄ＿ｓ
｝
ｒｅｔｕｒｎ（ｓ［［ｎ］］）
｝
ｓｑｒｔｓｅｑ（５０）
＞ ｓｑｒｔｓｅｑ（５０）
［１］ ＂ｓｑｒｔ（１＋ｓｑｒｔ（２＋ｓｑｒｔ（３＋ｓｑｒｔ（４＋ｓｑｒｔ（５＋ｓｑｒｔ（６＋ｓｑｒｔ（７＋ｓｑｒｔ（８＋ｓｑｒｔ（９＋ｓｑｒｔ（１０＋ｓｑｒｔ（１１＋ｓｑｒｔ（１２＋ｓｑｒｔ（１３＋ｓｑｒｔ（１４＋ｓｑｒｔ（１５＋ｓｑｒｔ（１６＋ｓｑｒｔ（１７＋ｓｑｒｔ（１８＋ｓｑｒｔ（１９＋ｓｑｒｔ（２０＋ｓｑｒｔ（２１＋ｓｑｒｔ（２２＋ｓｑｒｔ（２３＋ｓｑｒｔ（２４＋ｓｑｒｔ（２５＋ｓｑｒｔ（２６＋ｓｑｒｔ（２７＋ｓｑｒｔ（２８＋ｓｑｒｔ（２９＋ｓｑｒｔ（３０＋ｓｑｒｔ（３１＋ｓｑｒｔ（３２＋ｓｑｒｔ（３３＋ｓｑｒｔ（３４＋ｓｑｒｔ（３５＋ｓｑｒｔ（３６＋ｓｑｒｔ（３７＋ｓｑｒｔ（３８＋ｓｑｒｔ（３９＋ｓｑｒｔ（４０＋ｓｑｒｔ（４１＋ｓｑｒｔ（４２＋ｓｑｒｔ（４３＋ｓｑｒｔ（４４＋ｓｑｒｔ（４５＋ｓｑｒｔ（４６＋ｓｑｒｔ（４７＋ｓｑｒｔ（４８＋ｓｑｒｔ（４９＋ｓｑｒｔ（５０））））））））））））））））））））））））））））））））））））））））））））））））））＂
＞
"
SEIR MODEL
dS(t)/dt = mu*(N-S) - b*S(t)*I(t)/N - nu*S(t)
dE(t)/dt = b*S(t)I(t)/N - (mu+sig)*E(t)
dI(t)/dt = sig*E(t) - (mu+g)*I(t)
dR(t)/dt = g*I(t) - mu*R + nu*S(t)
mu:自然死亡率 b:感染率(S->I)
nu:ワクチン有効率(S->R) sig:発症率(E->I),g:回復率(I->R)
"
SEIRモデルのパラメータ
SEIR2 <- function(
# Parameters
contact_rate = 10, # number of contacts per day
transmission_probability = 0.01, # transmission probability
beta = contact_rate * transmission_probability, # tranmission rate
infectious_period = 20, # infectious period
gamma = 1 / infectious_period, # Prob[infected -> recovered]
latent_period = 5, # latent perior
sigma = 1/latent_period, # The rate at which an exposed person becomes infective
mu = 0, # The natural mortality rate
nu = 0 , # vaccination moves people from susceptible to resistant directly, without becoming exposed or infected.
Ro = beta/gamma, # Ro - Reproductive number.
# Initial values for sub-populations.
s = 99, # susceptible hosts
e = 0, # exposed hosts
i = 1, # infectious hosts
r = 0, # recovered hosts
# Compute total population.
N = s + i + r + e,
# Output timepoints.
timepoints = seq (0, 365, by=0.5),
)
今月号の数学セミナー
＊感染症数理モデル元年に機構と外挿の狭間に立つ……西浦 博 8
＊感染症数理モデル入門／SIRコンパートメントモデルと
基本再生産数……小林鉄郎・西浦 博 14
＊集団免疫論を超えて……稲葉 寿 19
＊国内の流行初期のデータによる予測とその評価……國谷紀良 26
＊大規模流行の発生確率にまつわる数理……安齋麻美・西浦 博 30
＊新型コロナウイルスの生体内感染動態の定量化とその応用／
数理科学で挑む新型コロナウイルス感染症治療の確立
……岩波翔也・キム・クァンス・藤田泰久・江島啓介・岩見真吾 33
＊感染症流行の収束にまつわる数理……ナタリー・リントン・西浦 博 40
そりゃ安倍売国奴が7年も居座るような国ですから
日本国民の多くは安倍の異常性に気付くの遅過ぎ
野党ガーパヨクガーで思考停止してきた罰だわ
低学歴総理の日本モデル
デマサポ「円高放置ガー」
現実は民主党政権は９２年以降、倒産件数最小です。
2012年（平成24年）の全国企業倒産1万2,124件
https://www.tsr-net.co.jp/news/status/yearly/2012_2nd.html >件数が過去20年間で最少の1万2,124件 円滑化法などの金融支援で抑制続く
経済馬鹿用語
1.財政ファイナンス（そんな言葉ねぇよｗ）
2.ハイパーインフレ（年間で7京円以上の物やサービスが買われないとならないよｗ）
3.インフレ制御不能（30年以上制御したくも無いのに制御出来ている国がある）
4.預金封鎖（憲法違反ですｗ）
5.国の借金（単なる貨幣供給量。返している国など無い。日本は少なすぎて不況）
Na <- 6.0022*10^23 # アボガドロ数
TCs134 <- 2.0652*365.2425*24*60*60 # 半減期（秒）
# λ:崩壊定数, 放射能A=-dN/dt=λN, N=A/λ=A*T/log2, λ=log2/T
(Cs134g_Bq <- TCs134/(log(2)*Na)*134) # Cs134:1ベクレルのグラム数
(Cs134Bq_pg <- (1/Cs134g_Bq)/(1*10^12)) # Cs134:1pgのベクレル
TCs137 <- 30.16171*365.2425*24*60*60
(Cs137g_Bq <- TCs137/(log(2)*Na)*137) # Cs137:1ベクレルのグラム数
(Cs137Bq_pg <- (1/Cs137g_Bq)/(1*10^12)) # Cs137:1pgのベクレル
# 半減期を秒で計算
# λ=log2/T
λCs134 <- log(2)/TCs134
λCs137 <- log(2)/TCs137
N0 <- 1
Cesium134 <- function(s){
N0*exp(-λCs134*s)
}
Cesium137 <- function(s){
N0*exp(-λCs137*s)
}
#原子数=放射能/崩壊定数=放射能/(log2/半減期)=放射能*半減期*log2
#放射能が同じなら原子数∝半減期
cesium_now <- function(Date=NULL,RCs134=1,RCs137=1){
t=ifelse(is.null(Date),as.numeric((Sys.Date()-as.Date("2011/3/11"))/365.2425)
,as.numeric(as.Date(Date)-as.Date("2011/3/11"))/365.2425)
TCs134 <- 2.0652 # half-life(year)
TCs137 <- 30.16171
# mol ratio
cs <- RCs134*TCs134*(1/2)^(t/TCs134) + RCs134*TCs137*(1/2)^(t/TCs137)
cs0 <- RCs134*TCs134 + RCs134*TCs137
ratio=cs/cs0
# radioavtivity ratio
# decay constant = log(2)/half-life
# ratioactivity ∝ decay constant * mol
CS <- (1/2)^(t/TCs134) + (1/2)^(t/TCs137)
CS0 <- TCs134 + TCs137
Ratio=CS/CS0
list(mol_ratio=ratio,radioactivity_ratio=Ratio)
}
cesium_now()
# 放射能比=1:1
TCs134 <- 2.0652 # 半減期(年）
TCs137 <- 30.16171
CS <- function(t) (1/2)^(t/TCs134) + (1/2)^(t/TCs137)
curve(CS(x),0,30)
uniroot(function(t,u0=1/2) CS(t)/CS(0)- u0, c(0,30))$root
GoTo初日（７月２２日）
東京・銀座のステーキ店「銀座ひらやま」
自民党の二階俊博幹事長らと会食。
①首相動静（７月２３日）
午前中は来客なく、私邸で過ごす。
午後も来客なく、私邸で過ごす。
②首相動静（７月２４日）
午前中は来客なく、私邸で過ごす。
午後６時から同１分、報道インタビュー
「国民は予防を徹底しろ」
③首相動静（７月２５日）
午前中は来客なく、私邸で過ごす。
午後も来客なく、私邸で過ごす。
④首相動静（７月２６日）
午前中は来客なく、私邸で過ごす。
午後も来客なく、私邸で過ごす。
7/30 医師会オコ会見「コロナに夏休みは無い」
米国債を売ろうした中川財務大臣はアメリカに抹殺された。
例の泥酔会見の直前、中川さんのワイングラスに薬を入れた実行犯も
正真正銘のCIAスパイ正力松太郎が作った読売新聞・日本テレビの記者「越前谷知子」「原聡子」と特定されてる。
ちなみに歴代首相で唯一、アメリカからの命令書（年次改革要望書）の受け取りを拒否した鳩山由紀夫元首相も
この直後からホワイトハウスからルーピー呼ばわりされ、電通CIA傘下のマスゴミもそれに追随、何の落ち度もないまま辞任に追い込まれた。
都合が悪い時は
定義を変える
解釈を変える
受け手側が勝手に勘違いした事にする
知らなかった事にする
想定外だった事にする
報告書を受け取らない
改竄する
隠蔽する
破棄した事にする
まわりが勝手に忖度した事にする
担当者が間違えた事にする
美しい国
感染者で「コロナはただの風邪」と言ってる奴がいない以上、感染してもない奴がただの風邪と泣き喚いたって何の説得力もない
だから自分が感染者になって証明するしかねーんだよ。
ただの風邪なら、かかったらところでリスクは低いんだからさぁ
鳩山のアメリカと中国でバランス取る外交は
日本の国益や防衛という意味でも別に悪くは無いと思うんだ
もう中国潰すなんて無理だし付き合うしか無いからな
>>466 尖閣を盗もうとしてる侵略国家とまともに付き合うのは無理。
Package ‘XXX’ was installed before R 4.0.0: please re-install it
.libPaths()
update.packages(ask=FALSE, checkBuilt=TRUE)
>>468 満州を奪おうとした日本もそう思わrているだろうよ。
まあ、元寇の損害賠償を！とか言い出せば面白いとは思うけど。
>>827 貼れと言われた気がするんで貼っておきますね
これが安倍内閣の功績
経済回せって
コロナ感染者が余計に増えて経済どん底。
残念ながら感染対策が最も有効な経済政策だとわからないアホの国が日本。
それを理解した中国は大量検査で制圧しているみたいだな。
>>473 人のブログなんて糞にもならないソースで偉そうに笑
>>475 政府なんぞ専門家という匿名ソースだぞ。
# 問題「4/5より大きく5/6より小さい分数で、分母がいちばん小さい分数はなに？」
fn <- function(lo=4/5,up=5/6){
i=1
flg=FALSE
while(flg==FALSE){
for(j in 1:i){
flg = lo<j/i & j/i<up
if(flg==TRUE){
ans=paste0(j,'/',i)
break
}
}
i=i+1
}
cat(ans)
invisible(c(j,i))
}
fn()
fn(3/4,13/17)
fn(1/2,16/31)
πの近似分数として
22/7= 3.142857
355/113= 3.141593
が知られている。
355/113より大きく22/7より小さい分数で、分母がいちばん小さい分数は何か？
仮分数でも計算できるように修正
fn <- function(lo=355/113,up=22/7){
i=1
flg=FALSE
while(flg==FALSE){
for(j in 1:ceiling(i*up)){
flg = lo<j/i & j/i<up
if(flg==TRUE){
ans=paste0(j,'/',i)
break
}
}
i=i+1
}
cat(ans)
invisible(c(j,i))
}
fn <- function(lo=355/113,up=22/7){
i=1
flg=FALSE
while(flg==FALSE){
for(j in 1:ceiling(i*up)){
flg = lo<j/i & j/i<up
if(flg==TRUE){
ans=paste0(j,'/',i)
break
}
}
i=i+1
}
cat(ans,'\n')
invisible(c(j,i))
}
fn(1/2,2/3)
fn(2/3,3/4)
fn(3/4,4/5)
fn(4/5,5/6)
fn(5/6,6/7)
fn(6/7,7/8)
fn(7/8,8/9)
fn(8/9,9/10)
# πの近似分数
fn(355/113,22/7)
現実は民主党政権は９２年以降、倒産件数最小です。
2012年（平成24年）の全国企業倒産1万2,124件
https://www.tsr-net.co.jp/news/status/yearly/2012_2nd.html >件数が過去20年間で最少の1万2,124件 円滑化法などの金融支援で抑制続く
経済回せって
コロナ感染者が余計に増えて経済どん底。
残念ながら感染対策が最も有効な経済政策だとわからないアホの安倍がリーダーの国が日本。
感染対策こそが経済政策と理解した中国は大量検査で制圧しているみたいだな。
# サイコロ6個振って目の合計が26を超える確率
library(gtools)
pm0=permutations(6,6,rep=T)
f<-function(x) sum(x) > 26
s=sum(apply(pm0,1,f))
S=nrow(pm0)
cat(s,'/',S,'\n')
s/S
#
dec2n <- function(num, N, digit = 6){
r=num%%N
q=num%/%N
while(q > 0 | digit > 1){
r=append(q%%N,r)
q=q%/%N
digit=digit-1
}
return(r)
}
pm=sapply(0:(6^6-1),function(x) dec2n(x,6))
f<-function(x) sum(x) > 26-6
s=sum(apply(pm,2,f))
S=ncol(pm)
cat(s,'/',S,'\n')
s/S
library(gtools)
library(fitdistrplus)
pm0=permutations(6,6,rep=T)
f<-function(x) sum(x) > 26
s=sum(apply(pm0,1,f))
S=nrow(pm0)
cat(s,'/',S,'\n')
s/S
d=apply(pm0,1,sum)
hist(d)
mean(d) ; var(d) ; sd(d)
fit=fitdistrplus::fitdist(d,'norm')
plot(fit)
table(d)
plot(table(d))
plot(table(d)/S,ann=F)
#
x=1:6
n=length(x)
(m=mean(x))
(SS=sum((x-m)^2))
(var=var(1:6)) ; SS/(n-1) ; SS/n
(sd=sd(x))
N=100
(M=m*N)
(Var=var*N)
(Sd=sqrt(Var))
curve(dnorm(x,M,Sd),N,6*N)
pnorm(3*N,M,Sd,lower=T)
>>486 サイコロ10回振って目の合計を当てる賭けをするときいくつにかけるのが最も有利か？
サイコロ100回振って目の合計が300未満の確率はおよそいくらか？正規分布表を使ってよい。
rm(list=ls())
source('toolmini.R')
library(gtools)
library(fitdistrplus)
N=6
(pm0=permutations(6,N,rep=T))
f<-function(x) sum(x) > 26
s=sum(apply(pm0,1,f))
S=nrow(pm0)
cat(s,'/',S,'\n')
s/S
d=apply(pm0,1,sum)
hist(d)
mean(d) ; var(d)
N*mean(1:6) ; N*sum((1:6-mean(1:6))^2)/N
fit=fitdistrplus::fitdist(d,'norm')
plot(fit)
table(d)
plot(table(d))
plot(table(d)/S,ann=F)
#
x=1:6
n=length(x)
(m=mean(x))
(SS=sum((x-m)^2))
(var=var(1:6)) ; SS/(n-1) ; SS/n
(sd=sd(x))
N=100
(M=m*N)
(Var=var*N)
(Sd=sqrt(Var))
curve(dnorm(x,M,Sd),N,6*N)
pnorm(3*N,M,Sd,lower=T)
コロナはただ風邪という人は唾をかけられても平気なのか？
「これでお前も感染した」英で唾かけられたタクシー運転手死亡
https://mainichi.jp/articles/20200523/k00/00m/030/075000c 駅係員、唾掛けられた後死亡 「感染」主張の男から―英
https://www.jiji.com/jc/article?k=2020051300657&;g=int
経済回せって
コロナ感染者が余計に増えて経済どん底。
残念ながら感染対策が最も有効な経済政策だとわからないアホの安倍がリーダーの国が日本。
感染対策こそが経済政策と理解した中国は大量検査で制圧して経済復活しているようだな。
サヨクの最終目標・・・移住・移民が自由にできる世界
安倍晋三・・・移民を受け入れる政策実施
サヨクの悲願を実現したということはサヨクのヒーローだから
ようは, 安倍＝パヨク＝ネトウヨ
ネットはパヨク内のネトウヨ派とパヨク派の内ゲバ.
仮病演技と憔悴アピールを用いるという情けない首相、
子供がズル休みしたい時、前もって体調悪いアピールをやり出しますよね。それと同じ気がしますよね
コピペだがなるほどと思った
>>
俺も発熱したけど、ダマで(ﾏﾏ)出勤してたよ
「風俗いったでしょ」って決めつけられて社会的に終わるからな
アレルギーで鼻水出てるってことにして、ふらふらでも押し通したよ
正直、それで通ってしまう世の中
休んだ不利益だけおっかぶせて、組織は責任を取らないという風潮
<<
不安な人は手軽に検査を受けられるようにして
陰性なら安心して旅行や帰省もできる、
陽性ならば不安なく仕事を休んで療養できる社会を作った国が勝者だろうね。
ケンサーズとか言っているような日本が負け組になるのは必至だな。
rm(list=ls())
# サイコロ10回振って目の合計を当てる賭けをするときいくつにかけるのが最も有利か？
# その確率は？
>>209 N=10
#
dicesum <- function(num, N=6){
r=num%%N
q=num%/%N
while(q > 0){
r=append(q%%N,r)
q=q%/%N
}
return(sum(r))
}
d35=0
i=0
while(i<6^N){
if(dicesum(i)==3.5*N) d35=d35+1
i=i+1
}
d35
6^N
d35/6^N
rm(list=ls())
# サイコロ10回振って目の合計を当てる賭けをするときいくつにかけるのが最も有利か？
# その確率は？
N=10
#
pipsum <- function(num, N=6){
r=num%%N
q=num%/%N
while(q > 0){
r=append(q%%N,r)
q=q%/%N
}
return(sum(r)+N)
}
dmax=0
i=0
while(i<6^N){
if(pipsum(i)==3.5*N) dmax=dmax+1
i=i+1
}
dmax
6^N
dmax/6^N
# sim
sim <- function(n=35) sum(sample(6,10,rep=T))==n
mean(replicate(1e5,sim()))
>>497 １０回程度では正規分布での近似はあてはまりがよくないな。
m=mean(1:6)
v=var(1:6)
M=10*m
V=10*v
SD=sqrt(V)
pnorm(35.5,M,SD)-pnorm(34.5,M,SD)
>>497 N10=10
#
pipsum <- function(num, N=6){
r=num%%N
q=num%/%N
while(q > 0){
r=append(q%%N,r)
q=q%/%N
}
return(sum(r)+N10)
}
dmax=0
i=0
while(i<6^N10){
if(pipsum(i)==3.5*N10) dmax=dmax+1
i=i+1
}
dmax # 4395456
6^N10 # 60466176
options(digits = 10)
dmax/6^N10 # 0.072692805974698974
N10=10
#
pipsum <- function(num, N=6){
r=num%%N
q=num%/%N
while(q > 0){
r=append(q%%N,r)
q=q%/%N
}
return(sum(r)+N10)
}
pip=numeric(6*N10)
pip[1:9]=0
i=0
while(i<6^N10){
idx=pipsum(i)
pip[idx]=pip[idx]+1
i=i+1
}
plot(pip)
# サイコロをn10個振ったときの目の合計の分布
n10=10
pipsum <- function(num, N=6){
r=num%%N
q=num%/%N
while(q > 0){
r=append(q%%N,r)
q=q%/%N
}
return(sum(r)+n10)
}
pip=numeric(6*n10)
i=0
while(i<6^n10){
idx=pipsum(i)
pip[idx]=pip[idx]+1
i=i+1
}
plot(pip)
>>501 グラフ化
data.frame(sum=10:60,pips=pips[10:60])
sum pips
1 10 1
2 11 10
3 12 55
4 13 220
5 14 715
6 15 2002
7 16 4995
8 17 11340
9 18 23760
10 19 46420
11 20 85228
12 21 147940
13 22 243925
14 23 383470
15 24 576565
16 25 831204
17 26 1151370
18 27 1535040
19 28 1972630
20 29 2446300
21 30 2930455
22 31 3393610
23 32 3801535
24 33 4121260
25 34 4325310
26 35 4395456
27 36 4325310
28 37 4121260
29 38 3801535
30 39 3393610
31 40 2930455
32 41 2446300
33 42 1972630
34 43 1535040
35 44 1151370
36 45 831204
37 46 576565
38 47 383470
39 48 243925
40 49 147940
41 50 85228
42 51 46420
43 52 23760
44 53 11340
45 54 4995
46 55 2002
47 56 715
48 57 220
49 58 55
50 59 10
51 60 1
Vectorにfreewareをアップロードしていると秀丸エディターを無料で使える特典がもらえたが当時はVzやWzを使っていたから、
アイコンのダサさがいやで使ってなかった。
Resource Hacker
http://www.angusj.com/resourcehacker/ を使ってアイコンデータを書き換えても使えた。
起動時にCRCやハッシュ値は照合していないようだ。
半角→全角の変換もできてまあ、便利だな。
薄型のノートってHDD交換とか手順が面倒だな。
ダウンロード＆関連動画＞＞
@YouTube 持ち出すことはまずなくて省スペース目的でのノートなら、厚手でバッテリー交換もねじ回しなしでやれる機種が楽だな。
買ってから気づいた。
powershell
Start-Process powershell.exe -Verb runas
reagentc /info
安倍政権は病気をたてにメディアを利用して騒がせて表に出ないようにして居るずるい政権
なんで最長政権になったか。
どんな不祥事があっても辞めないからだよ。
歴代首相には矜持があった。だから問題を抱えたら辞めた。
保守って何か？ 継続性だよ。自分が辞めても次の者が受け継ぐという確信、それが保守政治なんだ。安倍は自分のステージしか考えてない。
政治信条は受け継がれる、という発想すらないんだ。
ただの自己承認欲求が強いだけのガキだよ。
仮病演技と憔悴アピールを用いるという情けない首相
その安倍政権の雰囲気作りにまんまと乗せられるメディア
もうね、以前のようなインバウンドの幻影から目を覚ましたほうがいいよ 当分、旅館ホテルは無理だから 潰れるとこは潰れて淘汰されるよ で、潰れた処を中国資本が安く買って時を同じくして馬鹿政府が中国からの観光客の入国制限を緩和するシナリオだろ？ 所詮、中国贔屓の2Fの利権 分かり易いなw
Exp <- function(x,n=20) {
k=0:n
sum(x^k/factorial(k))
}
Exp(1)
exp(1)
Sin <- function(x,n=20){
k=0:n
sum((-1)^k*x^(2*k+1)/factorial(2*k+1))
}
Sin(1)
sin(1)
Cos <- function(x,n=20) {
k=0:n
sum((-1)^k*x^(2*k)/factorial(2*k))
}
Cos(1)
cos(1)
私立医大！私立医大！って自分で言ってた同じ医学部のブス彼女持ちの浮気男がいたな。
自分でイケメンと謳っていたが残念だったわ。
ちなみに、私立底辺医大と自分で豪語していたが底辺という文字が抜けていた。
面白い人がいるもんだね。
witoutコロナで三密で生産できるのが中国。
withコロナで三密を避けて生産する日本。
どちらが生産性がよいかは自明だと思う。
春節ウェルカムで疫病輸入して再入国規制もせずに強毒株も追加輸入、そして今はGOTOで全国に拡散。
すべては安倍の採った政策。
イギリスのジョンソン首相は感染して回復したけど
そこそこ症状重くて苦しかったから
それ以降コロナを舐めた発言はしてないんだよな
アホ層は自分が苦しい経験をしないと学習しない。
witｈoutコロナで三密で生産できるのが中国。
withコロナで三密を避けて生産する日本。
どちらが生産性がよいかは自明だと思う。
春節ウェルカムで疫病輸入して再入国規制もせずに強毒株も追加輸入、そして今はGOTOで全国に拡散。すべては安倍の採った愚策。
潰瘍性大腸炎患者の食事ｗ
キムチ・マッコリ・ホルモン
タバスコ
安倍総理大臣になってから
・過去最低の少子化を達成
・史上最悪のGDP成長率
・日本の憲政史上、最も実質賃金を引き下げた
・日本の憲政史上、最も実質消費を引き下げた
・日本の憲政史上、最も少子化を進め、人口を減らした
Windows Registry Editor Version 5.00
[HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Control\Keyboard Layout]
"Scancode Map"=hex:00,00,00,00,00,00,00,00,02,00,00,00,0e,00,45,00,00,00,00,00
num lockキーをback space(BS)に設定する。
Windows Registry Editor Version 5.00
[HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Control\Keyboard Layout]
"Scancode Map"=hex:00,00,00,00,00,00,00,00,02,00,00,00,0e,00,45,00,00,00,00,00
m=c(rep(0,9),1)
sim <- function(){
i=sample(10,1)
a=m[i]
j=sample(9,1)
b=m[-i][j]
c=m[-i][-j]
c(a,b,c)
}
replicate(5,sim())
安倍って詐病じゃないのか？
数々の虚言と不節制な食事をみると詐病の疑いが払拭できない。
自称潰瘍性大腸炎患者の食事
マッコリ・ホルモン
タバスコ
虚言のほんの一例
詐病じゃなければ
「安倍しかいない」と、ストレスで悪化する難病を抱える人に重責を押し付けてきた自民党は人権無視の政党ということになる。
安倍「持病が悪化したので総理大臣辞めます。（二回目」
英霊「国家国民の為ならば死にます。」
首相は自身の体調について、6月の検診で持病再発の兆候が見られ、7月に異変を感じるようになったと説明。
首相動静 会食 6月分
●6月19日 虎ノ門「ザ ダヴァン&ラウンジ」麻生、菅、甘利
●6月20日 永田町 レストラン「ORIGAMI」秘書官と食事
●6月22日 千代田区日本料理店「和田倉」細田元幹事長と
●6月24日 赤坂日本料理店「たい家」二階氏、林幹雄氏
●6月29日 永田町日本料理店「水簾」
首相動静 会食記録 7月分
●7月3日 日本料理店「もりかわ」JR東海葛西氏、北村氏
●7月21日 松濤仏料理店「シェ松尾」首相補佐官、外務審議官、秘書官
●7月22日 銀座ステーキ店「銀座ひらやま」二階幹事長、林幹雄氏、王貞治氏、杉良太郎氏他
●7月30日 丸の内日本料理店「和田倉」岸田氏と会食
そんなに悪いなら谷垣さんみたく議員も辞めてリハビリや療養に専念すべしよね
まともに働いたことが無いボンボンなのに
経済再生！
子供がいないのに
少子化解消！
東京の高級マンションに住んで
地方創生！
安倍総理の唯一の業績は
世襲の低学歴を総理にすると国が衰退する
ということを示したことだな。
羽田孜も低学歴だったが最短命だったから実害がなかった。
長期政権の秘訣
安倍晋三の主張
・検査増やす
・アビガン認める
・消費税は減税（森友問題が出てきてすぐに撤回）
厚労省の主張
・検査すんな
・アビガン認めんな
財務省の主張
・消費税増税
安倍なんか官僚の操り人形だよ
solve (a1-p)^2+(a2-q)^2=(b1-p)^2+(b2-q)^2,(a1-p)^2+(a2-q)^2=(c1-p)^2+(c2-q)^2 for p,q
p = (a1^2 (-b2) + a1^2 c2 - a2^2 b2 + a2^2 c2 + a2 b1^2 + a2 b2^2 - a2 c1^2 - a2 c2^2 - b1^2 c2 - b2^2 c2 + b2 c1^2 + b2 c2^2)/(2 (-a1 b2 + a1 c2 + a2 b1 - a2 c1 - b1 c2 + b2 c1))
q = -(a1^2 (-b1) + a1^2 c1 + a1 b1^2 + a1 b2^2 - a1 c1^2 - a1 c2^2 - a2^2 b1 + a2^2 c1 - b1^2 c1 + b1 c1^2 + b1 c2^2 - b2^2 c1)/(2 (-a1 b2 + a1 c2 + a2 b1 - a2 c1 - b1 c2 + b2 c1)) and -a1 b2 + a1 c2 + a2 b1 - a2 c1 - b1 c2 + b2 c1!=0 and a2 - c2!=0
bac <- function(B,A,C){ # 座標から角BACをラジアンで返す
if(is.complex(B)|is.complex(A)|is.complex(C)){ # 複素平面 1+2i
a=c(Re(A),Im(A)); b=c(Re(B),Im(B)); c=c(Re(C),Im(C))
}else{a=A;b=B;c=C} # 直交座標 (1,2)
ab=b-a
ac=c-a
dot=sum(ab*ac) # |ab|*|ac|*cos(θ) 内積
bac=acos(dot/sqrt(sum(ab^2))/sqrt(sum(ac^2))) # θ
return(bac)
}
oncircle <- function(A.B,C,D)
bac <- function(B,A,C){ # 座標から角BACをラジアンで返す
if(is.complex(B)|is.complex(A)|is.complex(C)){ # 複素平面 1+2i
a=c(Re(A),Im(A)); b=c(Re(B),Im(B)); c=c(Re(C),Im(C))
}else{a=A;b=B;c=C} # 直交座標 (1,2)
ab=b-a
ac=c-a
dot=sum(ab*ac) # |ab|*|ac|*cos(θ) 内積
bac=acos(dot/sqrt(sum(ab^2))/sqrt(sum(ac^2))) # θ
return(bac)
}
oncircle <- function(A.B,C,D){
bac(A,C,B)==bac(A,D,B)
bac <- function(B,A,C){ # 座標から角BACをラジアンで返す
if(is.complex(B)|is.complex(A)|is.complex(C)){ # 複素平面 1+2i
a=c(Re(A),Im(A)); b=c(Re(B),Im(B)); c=c(Re(C),Im(C))
}else{a=A;b=B;c=C} # 直交座標 (1,2)
ab=b-a
ac=c-a
dot=sum(ab*ac) # |ab|*|ac|*cos(θ) 内積
bac=acos(dot/sqrt(sum(ab^2))/sqrt(sum(ac^2))) # θ
return(bac)
}
oncircle <- function(A.B,C,D){
bac(A,C,B)==bac(A,D,B)
}
gr=expand.grid(1:3,1:3)
node=mapply(function(x,y) x+1i*y,gr[,1],gr[,2])
onCircle <- function(x) oncircle(x[1],x[2],x[3],x[4])
combn(9,4,onCircle)
円周角の一致でなくて半径と中心が一致することで同一円と判定するようにアルゴリズムを変更
N=7
gr=expand.grid(1:N,1:N)
(node=mapply(function(x,y) x+1i*y,gr[,1],gr[,2]))
tric <- function(A,B,C){ # 複素点３点を通る円の中心と半径を返す
a1=Re(A) ; a2=Im(A)
b1=Re(B) ; b2=Im(B)
c1=Re(C) ; c2=Im(C)
p = (a1^2*(-b2) + a1^2*c2 - a2^2*b2 + a2^2*c2 + a2*b1^2 + a2*b2^2 - a2*c1^2 - a2*c2^2 - b1^2*c2 - b2^2*c2 + b2*c1^2 + b2*c2^2)/(2*(-a1*b2 + a1*c2 + a2*b1 - a2*c1 - b1*c2 + b2*c1))
q = -(a1^2*(-b1) + a1^2*c1 + a1*b1^2 + a1*b2^2 - a1*c1^2 - a1*c2^2 - a2^2*b1 + a2^2*c1 - b1^2*c1 + b1*c1^2 + b1*c2^2 - b2^2*c1)/(2*(-a1*b2 + a1*c2 + a2*b1 - a2*c1 - b1*c2 + b2*c1))
Ce=p+1i*q
r=abs(Ce-A)
c(Center=Ce,Radius=r)
}
onCir <- function(x){ # 中心と半径が一致するかを返す
all(tric(node[x[1]],node[x[2]],node[x[3]])==
tric(node[x[1]],node[x[2]],node[x[4]]))
}
sum(combn(N^2,4,onCir),na.rm=TRUE)
７×７個だと
> sum(combn(N^2,4,onCir),na.rm=TRUE)
[1] 5704
6個まで数えました
ただもっとありそうなので教えてください
fn <- function(M=4,N=6){
gr=expand.grid(1:M,1:N)
(node=mapply(function(x,y) x+1i*y,gr[,1],gr[,2]))
tric <- function(A,B,C){
a1=Re(A) ; a2=Im(A)
b1=Re(B) ; b2=Im(B)
c1=Re(C) ; c2=Im(C)
p = (a1^2*(-b2) + a1^2*c2 - a2^2*b2 + a2^2*c2 + a2*b1^2 + a2*b2^2 - a2*c1^2 - a2*c2^2 - b1^2*c2 - b2^2*c2 + b2*c1^2 + b2*c2^2)/(2*(-a1*b2 + a1*c2 + a2*b1 - a2*c1 - b1*c2 + b2*c1))
q = -(a1^2*(-b1) + a1^2*c1 + a1*b1^2 + a1*b2^2 - a1*c1^2 - a1*c2^2 - a2^2*b1 + a2^2*c1 - b1^2*c1 + b1*c1^2 + b1*c2^2 - b2^2*c1)/(2*(-a1*b2 + a1*c2 + a2*b1 - a2*c1 - b1*c2 + b2*c1))
Ce=p+1i*q
r=abs(Ce-A)
c(Center=Ce,Radius=r)
}
onCir <- function(x){
all(tric(node[x[1]],node[x[2]],node[x[3]])==
tric(node[x[1]],node[x[2]],node[x[4]]))
}
sum(combn(M*N2,4,onCir),na.rm=TRUE)
}
fn(3,3)
fn(5,5)
fn(4,6)
fn <- function(M=4,N=6){
gr=expand.grid(1:M,1:N)
(node=mapply(function(x,y) x+1i*y,gr[,1],gr[,2]))
tric <- function(A,B,C){
a1=Re(A) ; a2=Im(A)
b1=Re(B) ; b2=Im(B)
c1=Re(C) ; c2=Im(C)
p = (a1^2*(-b2) + a1^2*c2 - a2^2*b2 + a2^2*c2 + a2*b1^2 + a2*b2^2 - a2*c1^2 - a2*c2^2 - b1^2*c2 - b2^2*c2 + b2*c1^2 + b2*c2^2)/(2*(-a1*b2 + a1*c2 + a2*b1 - a2*c1 - b1*c2 + b2*c1))
q = -(a1^2*(-b1) + a1^2*c1 + a1*b1^2 + a1*b2^2 - a1*c1^2 - a1*c2^2 - a2^2*b1 + a2^2*c1 - b1^2*c1 + b1*c1^2 + b1*c2^2 - b2^2*c1)/(2*(-a1*b2 + a1*c2 + a2*b1 - a2*c1 - b1*c2 + b2*c1))
Ce=p+1i*q
r=abs(Ce-A)
c(Center=Ce,Radius=r)
}
onCir <- function(x){
all(tric(node[x[1]],node[x[2]],node[x[3]])==
tric(node[x[1]],node[x[2]],node[x[4]]))
}
sum(combn(M*N,4,onCir),na.rm=TRUE)
}
fn(3,3)
fn(5,5)
fn(4,6)
>>459 終値ベースで7000円台は
小泉政権では２３日
麻生政権では４３日
民主党政権は０日
これで民主党は株価ガー経済ガーとなる理由がわからん
しかもデマサポは鳩山と菅を叩くが8000円台のほとんどは
デマサポが唯一評価する野田政権の時だし
安倍政権の実績
Chapter 1 潰瘍性大腸炎の食事の基本
www.mochida.co.jp/believeucan/enjoyfood/
脂肪の多い食品や揚げ物など、油を多く使用している料理は控えめに。
安倍「6月13日に定期検診で潰瘍性大腸炎が再発 と診断された」
https://www.tokyo-np.co.jp/article/51755?rct=politics
↓
その後、バターやチーズなどが基本のフランス料理を食いまくりw
●6月20日 永田町 レストラン「ORIGAMI」秘書官と食事
↑
フランス料理店
●7月21日 松濤仏料理店「シェ松尾」首相補佐官、外務審議官、秘書官
↑
フランス料理店
w 実は金持ちなんだよ
頭が悪いから大学受験失敗、仕方なく就職、夜間で法政へ
これだとゴミストーリーだから苦労人エピソードに改変
安倍晋三がストレス性の過敏性腸症候群を指定難病の潰瘍性大腸炎に改変したのと一緒
騙されるなよ
solve (sin(8/x)*sin(pi/3)/sin(pi*2/9))^2+(cos(8/x)*cos(12/x)+sin(8/x)*sin(12/x)*cos(pi/3))^2=1
x = 4/(2 π n + π) and n element Z
x = 2/(π n) and n<=-1 and n element Z
>>546 国家の教育への介入で憲法違反の虞があるよなぁ。
現在の65歳くらいの底辺私立医大卒の医師って
ほぼ全入の時代だったんでしょ。
お金さえあればほぼ全入だったんだって。
そういう医者から専門医を取れ！とか言われてもな。
欲しくないものは欲しくないので断ったら執拗に
嫌がらせされて、あることないこと院長に告げ口
されまくってウザいので結局辞めちゃった。
しかし食べ終わった弁当の空き殻などのゴミをゴミ箱に
捨ててたら、それを拾って来て俺の机の上に置かれてた
時はマジでビックリしたよ。
60歳半ばを過ぎた人間のやることじゃ無いよな。
>550
まともな医学部を卒業した人間なら、私立でも国立でもそういう職場で
働く機会はないでしょう。
流れ流れて地の果てですね。
カラオケで演歌でも歌うとぴったりですね。
>>551 いや東大出て官僚になったのに暗愚の安倍を養護する虚偽答弁をする羽目になった気の毒な人もいるよ。
そもそも3000万円とか5000万円とかいう法外な授業料を払わないと
卒業できないような大学がまともなわけがない。
>>554 そんな大金が払えるcategoryなら教育投資できたはず
金をかけても底辺シリツ医大へしか入れないのは
そういう頭脳ってこと。
>>554 そんな大金が払える家庭なら教育投資できたはず
金をかけても底辺シリツ医大へしか入れないのは
そういう頭脳ってこと。
Coefficient((sum[k=1,90]x^k)^10,x^100)
そもそも3000万円とか5000万円とかいう法外な授業料を払わないと
卒業できないような大学がまともなわけがないし、その上、女子学生と
多浪生は何の告知も無しに、勝手に合格が難しくなるように現役の
男子学生に加点（笑）。
それを指摘されると、大学側は現役の男子学生が優秀で、女子は
結婚するとすぐに子供が出来て家庭に入るから敬遠した、なんて
言い訳して開き直ってる（笑）。
大学の開学の祖も草葉の陰で泣いてるわ。
大学はそもそも勉強をしたいと言う意思を持ってる万人に対して開かれるべき。
3000～5000万円とか言う法外な授業料を払わないと卒業できないなんて本来の
大学のあるべき姿ではない。
国立も授業料が高すぎる。昔のように授業料を下げるべき。
私立もすべて国公立に変えるべき。
国家予算が云々いう輩がいるかもしれないけど、お金をかけるところを間違えてる。
全国の不法出稼ぎ外国人の隠れ蓑になってるFランを片っ端から潰せばよいだけ。
# 重複を許してｎ個からｒ個を選ぶ組み合わせを列挙する
fn <- function(n, r, v=1:n) {
if (r == 0)
NULL
else if (r == 1)
matrix(v, n, 1)
else if (n == 1)
matrix(v, 1, r)
else rbind(cbind(v[1], fn(n, r - 1, v)), fn(n - 1, r, v[-1]))
}
実例
> fn(3,4)
[,1] [,2] [,3] [,4]
[1,] 1 1 1 1
[2,] 1 1 1 2
[3,] 1 1 1 3
[4,] 1 1 2 2
[5,] 1 1 2 3
[6,] 1 1 3 3
[7,] 1 2 2 2
[8,] 1 2 2 3
[9,] 1 2 3 3
[10,] 1 3 3 3
[11,] 2 2 2 2
[12,] 2 2 2 3
[13,] 2 2 3 3
[14,] 2 3 3 3
[15,] 3 3 3 3
>>561 政治家とか官僚の天下り先にFラン私立大が使われているからなぁ。
中韓とパヨクをディスって悦にいっている自称「保守」が安倍の暗愚政治を許したようなものだな。
組み合わせの問題で教えて下さい。
①～⑩の名前のついた箱があります。
一つの箱には最低１以上～９１以下の数字が入ります。
このとき、１０個の合計が必ず１００になる条件とした場の組み合わせを
求める方法はあるでしょうか。
1個ずつ玉の入った名前付きの箱を10個用意して、その箱にあと90個の玉を入れるのと同じことだから、
10個の箱から重複を許して90回選ぶ選び方と同じ
なので重複組合せ
f <- function(Box,Sum){ # Box:箱の数,Sum：入った数字の合計の値
# 重複を許してｎ個からｒ個を選ぶ組み合わせを列挙する
H <- function(n, r, v=1:n) {
if (r == 0)
NULL
else if (r == 1)
matrix(v, n, 1)
else if (n == 1)
matrix(v, 1, r)
else rbind(cbind(v[1], H(n, r - 1, v)), H(n - 1, r, v[-1]))
}
h=H(Box,Sum-Box) # Box個の中から重複を許してSum-Box個を選ぶ
nh=nrow(h) # その組み合わせ数
re=matrix(rep(NA,Box*nh),nrow=nh,ncol=Box) # メモリ確保
a=numeric(Box)
for(i in 1:nh){ # 各々の選び方iに対して
for(j in 1:Box) a[j]=sum(j==h[i,]) # どの箱が何個選択されたかを
re[i,] =a # reのi行に入れる
}
return(re+1) # 1から始まる分を補正
}
f(Box=3,Sum=9)
f(Box=10,Sum=100)
> f(Box=3,Sum=9)
[,1] [,2] [,3]
[1,] 7 1 1
[2,] 6 2 1
[3,] 6 1 2
[4,] 5 3 1
[5,] 5 2 2
[6,] 5 1 3
[7,] 4 4 1
[8,] 4 3 2
[9,] 4 2 3
[10,] 4 1 4
[11,] 3 5 1
[12,] 3 4 2
[13,] 3 3 3
[14,] 3 2 4
[15,] 3 1 5
[16,] 2 6 1
[17,] 2 5 2
[18,] 2 4 3
[19,] 2 3 4
[20,] 2 2 5
[21,] 2 1 6
[22,] 1 7 1
[23,] 1 6 2
[24,] 1 5 3
[25,] 1 4 4
[26,] 1 3 5
[27,] 1 2 6
[28,] 1 1 7
エロ夫妻は同伴で最近パーティに出席し、そこには他の3組の夫婦が同伴で出席していた。いろいろな人々の間で接吻が行われた。
どの人も自分の同伴者とは接吻をせず、どの人も同じ人と2度以上は接吻をせず、また当然だが、誰も自分自身とは接吻をしなかった。
接吻をしたあと、エロ氏は彼の妻を含めた各人に、他人と何回接吻をしたかと尋ねた。驚いたことには、どの人も異なる回数を答えた。
さて、エロ夫人は何回接吻をしただろうか。
>>568 n=8
(co=combn(n,2)) # 8人から2人選ぶ
(pair=co[,-c(1,14,23,28)]) #(1,2),(3,4),(5,6),(7,8)は除外して24通り
# 2^24=16777216通りの組み合わせ
f <- function(num,digit=24){ # numを24桁の2進数で表示
N=2
r=num%%N
q=num%/%N
while(q > 0 | digit > 1){
r=append(q%%N,r)
q=q%/%N
digit=digit-1
}
shake=numeric(n) # 握手した人数の数列 1:イナ氏 2:イナ夫人
for(i in 1:n) shake[i]=sum(r[pair[1,]==i | pair[2,]==i])
if(all(0:7 %in% shake[-1])){ #イナ氏以外の握手人数がすべて異なれば
return(shake[2]) #イナ夫人の握手人数を返す
}
}
y=sapply(0:(2^24-1),f)
y
rm(list=ls())
library(gtools)
pm=permutations(2,24,0:1,rep=TRUE)
n=8
co=combn(n,2)
pair=co[,-c(1,14,23,28)]
g <- function(r){
shake=numeric(n)
for(i in 1:n) shake[i]=sum(r[pair[1,]==i | pair[2,]==i])
all(0:7 %in% shake[-1])
}
y=apply(pm,1,g)
pm[y,][,1:2]
>>568 rm(list=ls())
n=8
(co=combn(n,2)) # 8人から2人選ぶ
(pair=co[,-c(1,14,23,28)]) #(1,2),(3,4),(5,6),(7,8)は除外して24通り
# 2^24=16777216通りの組み合わせ
library(gtools)
pm=permutations(2,24,0:1,rep=TRUE)
n=8
g <- function(r){
shake=numeric(n)
for(i in 1:n) shake[i]=sum(r[pair[1,]==i | pair[2,]==i])
all(0:6 %in% shake[-1])
}
y=apply(pm,1,g)
(yi=which(y))
# demo
rbind(pair,pm[yi[1],])
SHAKES=NULL
for(j in 1:length(yi)){
zj=rbind(pair,pm[yi[j],])
shake=numeric(n)
for(i in 1:n) shake[i]=sum(zj[3,][pair[1,]==i | pair[2,]==i])
SHAKES=rbind(SHAKES,shake)
}
rownames(SHAKES)=NULL
SHAKES
エロ夫妻は同伴で最近パーティに出席し、そこには他の3組の夫婦が同伴で出席していた。いろいろな人々の間で合体が行われた。
どの人も自分の同伴者とは合体をせず、どの人も同じ人と2度以上は合体をせず、また当然だが、誰も自分自身とは合体をしなかった。
合体をしたあと、エロ氏は彼の妻を含めた各人に、他人と何回合体をしたかと尋ねた。驚いたことには、どの人も異なる回数を答えた。
さて、エロ夫人は何回合体をしただろうか。
rm(list=ls())
n=8
(co=combn(n,2)) # 8人から2人選ぶ
(pair=co[,-c(1,14,23,28)]) #(1,2),(3,4),(5,6),(7,8)は除外して24通り
# 2^24=16777216通りの組み合わせ
library(gtools)
pm=permutations(2,24,0:1,rep=TRUE) # pairが握手をしたかの数列
n=8
g <- function(r){
shake=numeric(n) # 握手した人数の数列
for(i in 1:n) shake[i]=sum(r[pair[1,]==i | pair[2,]==i])
all(0:6 %in% shake[-1]) # 握手した人数が異なるか
}
y=apply(pm,1,g)
(yi=which(y)) # 48通り
# demo
demo <- function(k=sample(48,1),CEX=3){
(y1=rbind(pair,pm[yi[k],]))
plot(y1[1,],y1[2,],xlim=c(1,8),ylim=c(1,8),bty='l',ann=F,
pch=ifelse(y1[3,]==1,'○','×'),cex=CEX)
points(y1[2,],y1[1,],
pch=ifelse(y1[3,]==1,'○','×'),cex=CEX)
points(1:8,1:8,pch='×',cex=CEX)
points(c(1,3,5,7),c(2,4,6,8),pch='×',cex=CEX)
points(c(2,4,6,8),c(1,3,5,7),pch='×',cex=CEX)
}
layout(1); demo()
par(mfrow=c(4,4))
for(k in 1:16) demo(k,1.5)
for(k in 17:32) demo(k,1.5)
for(k in 33:48) demo(k,1.5)
layout(1)
#
SHAKES=NULL
for(j in 1:length(yi)){
zj=rbind(pair,pm[yi[j],])
shake=numeric(n)
for(i in 1:n) shake[i]=sum(zj[3,][pair[1,]==i | pair[2,]==i])
SHAKES=rbind(SHAKES,shake)
}
rownames(SHAKES)=NULL
SHAKES
中学入試の方が医師国家試験より圧倒的に難しいなぁ。
同じ大きさのコインが10枚あり，9枚は鎖状につながって並んでいます。図のように，
コインCを9枚のコインのまわりをすべることなく回転させます。ただし，その途中で9枚全部に接していきます。
一周してもとの位置にもどるまでに，コインCは何回転するでしょうか。
http://sansuu.ciao.jp/essei/img43/image75[1].jpg
同じ大きさのコインが10枚あり，9枚は鎖状につながって並んでいます。
図のように，コインCを9枚のコインのまわりをすべることなく回転させます。
ただし，その途中で9枚全部に接していきます。
一周してもとの位置にもどるまでに，コインCは何回転するでしょうか。
こうやってまとめると、安倍政権って菅直人以後の民主党政権の延長だな。
図のように半径2cmの円が6個あります。となり合う円はすべてぴったりとくっついているとします。周りにひもをたるまないようにかけました。
このひもの長さを求めなさい。
http://sansuu.ciao.jp/essei/img43/image89[1].jpg
有事に仮病で逃げた首相、、、
【あれぇ？おかしいぞ】
6月13日
定期検診で潰瘍性大腸炎が再発
https://www.tokyo-np.co.jp/article/51755?rct=politics ↓
6月19日
安倍首相、ステーキ馬鹿食い
https://www.fnn.jp/articles/-/77180 その会食とは６月19日の夜に都内のホテルで行われた、安倍首相・麻生副総理・菅官房長官と甘利氏の4人での会合だ。
甘利氏はこんな裏話を披露した。
安倍首相との会食・6月19日
「最後の方にステーキが出たんですよね。（安倍首相は）ものすごい食欲があって出された肉はきれいに平らげられていました。
私はだいたい食べてるうちに『もういいかな』ってなるんですけれども。
総理と今まで何度も会食でご一緒しましたけれど、肉が出たら全部平らげますね」
library(gmp)
n=as.bigz(1476250)
ans=NULL
while(n<1e7){
m=as.bigz(1+3^n)
if((m%%n)==0){
print(n)
ans=append(ans,n)
}
n=n+10
}
ans
#include <stdio.h>
int main()
{
long a,b,c,d;
for(a=1000000;a<=10000000;a++){
for(b=a,c=3,d=1;b>0;b=b/2){
if (b%2 ==1) d = (d*c) % a;
c=(c*c) % a;
}
if (d + 1 == a){
printf("%d\n",a);
}
}
printf("done\n");
}
f <- function(lo=1,up=1e4){
a=lo
while(a<=up){
b=a
c=3
d=1
while(b>0){
if((b%%2)==1) d=(d*c)%%a
c=(c^2)%%a
b=b/2
}
if((d+1)==a) print(a)
a=a+1
}
}
f()
#include <stdio.h>
int main()
{
long a,b,c,d;
for(a=1000000;a<=10000000;a++){
for(b=a,c=3,d=1;b>0;b=b/2){
if (b%2 ==1) d = (d*c) % a;
c=(c*c) % a;
}
if (d + 1 == a){
printf("%d\n",a);
}
}
printf("done\n");
}
f <- function(lo=1,up=1e4){
a=lo
while(a<=up){
b=a
c=3
d=1
while(b>0){
if((b%%2)==1) d=(d*c)%%a
c=(c^2)%%a
b=b/2
}
if((d+1)==a) print(a)
a=a+1
}
}
f()
f <- function(lo=1,up=1e7,by=1){
for(a in lo:up){
b=a; c=3; d=1
while(b>0){
if((b%%2)==1) d=(d*c)%%a
c=(c*c)%%a
b=b%/%2
}
if((d+1)==a) cat(a,'\n')
a=a+by
}
}
f(1,10000)
f(10,1e8,10)
# 自然数nで「1+3^n は nで割り切れる」を満たすものはすべて分かりますか？
rm(list=ls())
library(gmp)
n=as.bigz(1)
ans=NULL
while(n<1e5){
m=as.bigz(1+3^n)
if((m%%n)==0){
print(n)
ans=append(ans,n)
}
n=n+1
}
ans
# 謎のアルゴリズム
f <- function(lo=1,up=1e7,by=1){
for(a in lo:up){
b=a; c=3; d=1
while(b>0){
if((b%%2)==1) d=(d*c)%%a
c=(c*c)%%a
b=b%/%2
}
if((d+1)==a) cat(a,'\n')
a=a+by
}
}
f(1,10000)
# 10の倍数らしいので
f(10,1e8,10)
# if((1+3^a) %% a == 0) print(a)
fn <- function(a,print=F){
b=a; c=3; d=1
while(b>0){
if(print) print(c(b,c,d))
if((b%%2)==1) d=(d*c)%%a
c=(c*c)%%a
b=b%/%2
}
if((d+1)==a) {
if(print) print(c(b,c,d))
cat(a,'\n')
}
}
fn(50,T)
日本の医療レベルが低いってことか？
862 卵の名無しさん 2020/09/07(月) 12:29:41.15 ID:hUXvwdzt
日本は昨日までコロナでの死者数が1357人で、韓国は334人、中国は4634人…
韓国と比べて人口は約2.4倍なのに死者数が4.1倍、中国の人口の9%なのに死者数が29.2%でダメだな
dアカウントは複アカ作り放題
dアカウントと口座との紐付けに本人確認がない
勝手に作られたdアカに口座紐付けされて引き出されてる。
【NTTドコモ】中国銀行でも #ドコモ口座 を利用した不正利用が発生 [WATeR★]
http://2chb.net/r/newsplus/1599493554/333 333 名前：不要不急の名無しさん[] 投稿日：2020/09/08(火) 02:32:29.51 ID:4j6hyZlO0
>>234 1. 口座番号のリストを作成する(銀行によっては作成順の連番？)
2. 口座番号をもとに、振り込み処理を途中まで掛けて氏名を確認
3. ↑で確認した氏名でdアカウントを作成
4. dアカウントに口座番号、氏名、固定の暗証番号(0101 とか)で登録をトライ
これを1万アカウント繰り返したら…
ドコモの本人確認が甘いのと、地銀のセキュリティ対応が甘いところを突いてる。
生年月日や登録電話番号なりで多要素認証がある銀行には通用しないよ。
最近、通帳やキャッシュカードのコピーを添付して、氏名や生年月日をどこかに伝えませんでしたか？
暗証番号抜かれてもキャッシュカードや通帳は盗まれてないから平気と思ってたらキャッシュカードもどきをドコモが提供していた。
最近、通帳・キャッシュカード・免許証のコピーを添付して、
氏名や生年月日をどこかに伝えませんでしたか？
自分の口座から引き落とし契約されている対象のサービスリストが
なぜ金を払ってる本人に提示されないのかがわからん
どんな理由で非公開なんだ
こんなもん銀行サイトのマイページに普通に掲載してていいめっちゃ基本情報なのに
それ掲載したら一体どんな不都合があるんだ。
Dux8sUjezkRK4t0E1qWdce8od8t674zQJ6LF7Hq1B5mb3M6UkJXKzHp3LhteyQRGUG2bqZmlVrEyjofViZoTO2m7fwJUokuNJ1OdvYUvQG2FTbif1jAnuhpebinmw71UJgoA1T5Q9dpqduMsZFRP3ZsXHSIa5n6jC7r92NDX5aYf2jabDbCiUoojR2ddnmn2TgjTvcTyHQq4yJacPtGs9SOQfPjCBn2QQCgZX0sKQZdTUKx6oY6MJWJrbitORoNbmvCtPDGTescHSWfPkT3buydBOA7ijY9c5deh0mcMTCo13urKc4bpDYA0JDnz4u6WbmtspwhAYpixuhiNlDFEE6MaF5vmueqwyavH1XwWicxBd6TuYU1s88WVLZ7ygQOqomafg6o65kfdsbRo2unuAWSXyuhd1iYbYmrsNGPQnwgUUrBIB5IiV4qkF6zW5t5dnhtYIENokZsgVre9R65nxqhClFfK0fvNlCI9XjcbhEmbmdn7fDFhx3PyyEJZB7oKGCWTFDJbhmcrRhAXX6XTl1QprrHBwwr8oKjKE2lQH5TUop4kILMJYd113BJvLUfVcW0Vrt26AgZ8BvWERmjoIBhld8yDSYRAdsZhoKy0YQZcnwEkeLE8ZurQTH8R9NwpeLfi7pRCWloS3T8qdUFPzKxduoohC8saGhUJ0WIC6iismxcWF9P46XtKpNfYTdRvmT0ZF1niYsOzIke0foq2WEW6zpJXNBCmyI9bTvO8dLeG8OgkYNKsdAnBJSAYXwAA7JT3qZCkJUdOuWEOeKkHWlZWWcypbMW8LqMNg0Gzly83FS5GU9Wd3Ldq1bJkzu5GmS88aCps19XjpHwd6a1GYiwSCFPvsmFj23taBv66eOIvqEVACmPDS0mmWuptvz4ALnvPBkBZlH7wbki7gybEczoYgC3bALf0gEcNotleTIx21SG3YSFNitZExyhPRcBT5anYO3ifruThSbylCj9i6vtlAwS3cHN8qp7bE47z
1500桁のパスワード
zDcQsMwbarLQNVbaFCmwDiaKvH9q44IvGVsKUoCDO0Rs0DXjDOXLRY7PYUGqUerqyJ4OvPKZPIuWl6OIqs8ZSkZCwrc1IDHgDHVjqrsbj5XeKsAtMCp6133KRNUX8uoK7t6DKIQ0VoywgHVAsAKj3WZK5n8VZK44lFTELvbuC4aVVYkEEOmlXPGDoEfoJxDtIKloau20vo9QDuxu9s8UjezkRK2UtkERqWdmKhdrvWZfBQxmeIf0Th4GjzKdhAkudYynwhm2B8Knud81Ni3ZLCSl7a6eHYP6So2JWwK9UHwacjMjJISkjnu7E7Z3kBClXcg31WDwHYerWrY3FIbT6xz2sWxQBRdR4rpimaY7LZWjw9gTOTYKfAfFLCgC8bDeLD6CoMrFwCIQMsMUZgbEyCWxwGYesgY9D46mLR1fSRxBLbwDtOQiBnghxX3CwSrtd0SyERh1EuGgRfu6lRQRaGUppLorl2LlryuguVfCv2hwwDdoqNtUemzUc2cLSN9MEdwzGBzn0ZzmWeFZF6WCgnPJ3ZUbGcyI73vUjWKGuEqBB58FbRPXpzVbkcDHkZQmUaTF0x2NbO0Bo2cqUnOEm43a55FLCjhbxyyefqhP4KwR5krwduNDAzpEB57DmW5fvlS9XA2Sj90prdPn33by1P7ktUbPUCNB7aWahNcWeVJ8Vro9oeafzdXIaiR5uP5dbbyb24kYAsWqQgyhWaxL3X7obozw8PrPODYB3tXMCWU64b31hnMRoDowODano3UddCrg5d2yjT9qYwzyXaez87B8oVEVSCzw2mF1pDRNoimMUEFQkW3V3BS1zHWYdC4f1bpDlXbGMT75nis2k21b6o6NahWk2Yle6gbAwpbHDhnU30x9Ph6XLM7hFHsCGPqDxzTE3UmidnkX8E2qzcNH6ILmimXLlPMJClQwCnxHDBe7TSy22nClwYxQ2h2TAMWJha1xOHxTlCKWNtGpTMoSpYpvAUcBdcE6A5Awbqp4jbqukiDr4Tf69Kb5WEfRfn343L38svFO0Ylp7x6CwFdy8uUqFUz06yV3v5YDrIyuxBaLLAtxQ0DTbsHgxfQiePTpSEmmKxG4Saz9R3RfRdceY2GS7dc9GlAxP7tdz4y5qkEOfH2H4FRLw55z95PKosMJtlTC6zzXoSJBe9jcvqHqUyYDkg24HjtTj86uSpuvihX3xol4vJsIE2tfegsJW6EhqUeJL6CV17JPeFBaDqUqnAyysFJiHF7h43wyXMcXLQduwZBpqrGdzV6UlKhvice3qa6galoCYOGE2C2wpfOesqdRTW0w64mdktcp7JWirLGwY69FXr4Hc3mjXZn3k4Rdjr392WU38XXxUnBy1bPohAbUlVPU6AbaCurk3i00Gf2LRxs8zVXaBU8SZ270uqE10NKPvSpNj6be1ZaWZjlCupgQut3Dg6CDl0vO6hdpGMcrEGSPVtXxjYjtsG186xCEWZQNY4JdOF9Sev056BDkTWI2Q656
random <- function(n=16,char=c(LETTERS,letters,0:9)){
rep=ifelse(n>length(char),TRUE,FALSE)
re=paste0(sample(char,n,replace=rep),collapse='')
cat(re,'\n')
invisible(re)
}
random(1500)
> random <- function(n=16,...){
+ char=c(LETTERS,letters,0:9,as.character(c(...)))
+ rep=ifelse(n>length(char),TRUE,FALSE)
+ re=paste0(sample(char,n,replace=rep),collapse='')
+ cat(re,'\n')
+ invisible(re)
+ }
> random(100,c('_','.','*'))
4kOf2HRLw5595KostlTzXBejcHqg24jT86uSuvhXxolvsItfe6UJ6CV7JeFaqqn*yFJH4wyXMcXLQwBprGdzV6Uvie3a6goY_wOs
悲惨ですよ、私立医は。
長男が私立医、今春、次男も私立医の医師会会員なんか、
コロナ不況の中、もう哀れで、哀れで・・・・
そもそも3000万円とか5000万円とかいう法外な授業料を払わないと
卒業できないような大学がまともなわけがない。
聖マリアンナとかいう医大のなかのキングオブ底辺
こんなとこに多浪して入るとかどんだけ学力低いんだよw？
地頭悪いんだろうな
マジでクソだわ
生きてて恥ずかしくならねーのかな？あいつ
いじめられっ子が
マジで腸が煮えくりかえるな
サイコ野郎が
4 + 2sin(x) + 2cos(y) + sin(x) cos(y) - cos(x) sin(y)
(sin(y)-cos(x))^2 + (sin(x)+cos(y))^2 +(1+sin(x))^2+ (1+cos(y))^2
架空求人で履歴書かき集めれば個人情報売買できる
そういう企業が今たくさんある
５ｃｈで噂になってる企業あるよね
履歴書よりウェブ応募がいいね
ある外資系企業の下請は幽霊法人で国外のクラウドサービスに被保険者番号からマイナンバーまで保管
国外は個人情報保護法の対象外なんだと
間抜けな法律のお陰で個人情報は国外保管
きっと中国にもたくさんある
法人サポートが中国の場合、法人口座や拠点住所一覧も中国に握られている
契約のみデータセンターからすべてアウトソース依存国家の末路は怖い
>>608 確か37か38くらいだったかな？w
なんちゃって外科医やってるよ
ビビるよ？wクッソ無能だからなw
前々スレからのド底辺シリツ医への宿題
若い女性研修医（嘘つきかどうかは不明）から
「あなたのいうことが正しければ手コキかフェラをしてあげる、そうでなければセンズリを命じる」と言われた。
フェラをしてもらうには何と言えばいいか？
>>609 しかもありとあらゆる工作隠蔽してるっていうねw
内科の領域もみれますみたいな装ってる無能w
もはや人殺しだなw
あんなのを救急で見させるとか病院もどうかと思うけどなw
病院ぐるみでやってんだろうなw
>>612 ＞内科の領域もみれます
ド底辺シリツ医大卒なので内科のことはさっぱりわかりません、と言えば誰もが納得してもらえるのに
やっぱり、頭が悪いんだね。
>>614 最悪な治療施されたからね
初めから受け入れるなと
あそこまでのヤブは見たことないわ
適当な診察ばっかしてんだろうな
医学部は最低でも早慶理工以上の学力ないと
入れないようにしないと
不幸な人間がうまれるだけだわ
>>612 で、まさかそいつとその家族はのうのうと生きてるのか？ 人の家族を滅茶苦茶にして？
それは許されないだろ普通に
どうなんだ？
公文書改竄するような今の政権下で国勢調査に協力したくないなぁ。
記者 「10年間くらい(消費税)引き上げなくてもいいという、その根拠ついては何だと考えられているのか」
菅 「まさに、アベノミクスを推進をし、経済を成長させる。まさに、経済成長…え…経済を再生させると、させなければ、財政健全化ないという、その政策のである」
アベちゃん以上にひどいじゃないか。完全に耄碌ジジイ。
安倍のほうがマシだったという時代が来そうだな。
記者 「10年間くらい(消費税)引き上げなくてもいいという、その根拠ついては何だと考えられているのか」
菅 「まさに、アベノミクスを推進をし、経済を成長させる。まさに、経済成長…え…経済を再生させると、させなければ、財政健全化ないという、その政策のである」
アベちゃん以上にひどいじゃないか。完全に耄碌ジジイ。
安倍のほうがマシだったという時代が来そうだな。
ダウンロード＆関連動画＞＞
@YouTube
1分15秒あたりから >>616 生きてんじゃねｗ
私立医大って事は父親も医者かそこそこの会社かだろ
ご両親がご健在なのか是非知りたいとこではあるなw
お宅の息子さんについてどうお考えなのかｗ
面拝みたいものだ
まぁカルマは深いだろうなｗ
何れにせよこれからさ これから始まる
こういうのは裏口シリツ医には解けないと思う。
司法試験予備試験の問題から、
球面上の異なる 2 点間の球面に沿った最短距離は，大円（球の中心を通る平面と球面が交わって共有する円）のそれら 2 点を端点とする弧の（長くない方の）長さである。地球上で北緯 45 度・東経 145 度，北緯 45 度・西経 125 度に位置する 2 地点間の地表面に沿った最短距離として最も近いものを，次の1から5までの中から選びなさい。ただし，地球は半径 6378 km の球とする。
1．5009 km 2．6679 km 3．8348 km 4．9017 km 5．9876 km
fn <- function(
ai=45, # 北緯°
ak=145, # 東経°
bi=45, # 北緯°(南緯はー°)
bk=-125){ # 東経°(西経はー°)
R=6378 # 地球の半径km
u=pi/180
A=R*c(cos(ai*u)*cos(ak*u),cos(ai*u)*sin(ak*u),sin(ai*u))
B=R*c(cos(bi*u)*cos(bk*u),cos(bi*u)*sin(bk*u),sin(bi*u))
AB=sqrt(sum((A-B)^2))
asin(AB/(2*R))*2*R
}
fn()
試験会場で計算しやすいように問題では数値設定してあるなぁ。
大塚とかいうヤブぱねー
歯を食いしばって苦しめばいいのな
てめえとてめえの家族がな
許さねーからな お前だけは
大塚君元気にされてるかな。
アッチ系の先生だったけど
良い人だったな～。
HP
コンピューターの電源を入れるか、再起動します。 画面に何も映っていないうちに、[F10] キーを押して BIOS 設定メニューに入ります。
BIOS 設定メニューは、一部のコンピュータにf2またはf6キーを押すことによりアクセス可能です。 BIOSが開いたら、ブート設定にアクセスします。
HPはロゴがでるまえにf10とは、大抵はロゴがでたらdeleteかf2だと思っていたのだが、特殊だなぁ。
Dell
BIOS セットアップの起動
ノートPC の電源を入れます（または再起動します）。
Dell のロゴが表示されたら、次のいずれかのアクションを実行し BIOS セットアッププログラムを起動します。 キーボードあり ? 「BIOS セットアップを起動」メッセージが表示されるまで、<F2> をタップします。
緊縮財政・構造改革・観光立国
この三つで衰退途上国日本の没落必須だな。
６日の参院予算委員会で、立憲民主党の小西洋之議員が安倍晋三氏に「安倍総理はよく『法の支配』とおっしゃいますが、法の支配の対義語は何ですか？法の支配の反対の意味の言葉は何ですか。」と尋ねたところ、安倍晋三氏は「まさに、反対語と言うよりも、法の支配、え、ということを申し上げているのはですね、あわば、あ～この～この海、まさに法の支配による、この国際秩序を維持し、平和な海を守っていくことが、それぞれの海の反映に繋がっていく、という考え方を示しているところでございます。」と、トンチンカンな答弁を行ってしまいました。
小西議員は「法の支配の対義語は、憲法を習う大学の１年生が一番最初の授業で習うことですよ。」と、法の支配の対義語を知らない安倍晋三氏に対し、「憲法がよって立つ基本原理すら理解せずに改憲を唱えている安倍総理に教えて差し上げます。法の支配の対義語は『人の支配』です。権力者の専断的行為によってルールをねじ曲げて、国民の権利や自由を侵害する、そういう時代がかつて人類にあったから、近代立憲主義に基づく憲法をつくる。その近代主義の憲法の基づく理念が『法の支配』の原理なんですよ。」と話し、立憲主義に基づく憲法の基本的な考え方を諭しました。
『法の支配』の対義語が『海の平和を守る』とは・・・。
『法の支配』の対義語が分からないのなら、『法の支配』の本当の意味も知らないということことなのではと疑いたくなります。
辺野古を見てもそのとおりではないでしょうか。
安倍晋三氏は、成蹊大学政治学部卒業という学歴を持っています。
近代民主主義の基本は立憲主義であり、そのことからも憲法について学ぶことは、政治学を学ぶうえで「いろはのい」であるはずです。
この方は本当に大学で政治学を修めてきたのでしょうか。
地球の大きさは，紀元前３世紀頃にエラトステネスによって初めて求められた。
アレキサンドリア 北緯31.20194ﾟN 東経29.91611ﾟE
アスワン 北緯24.08889ﾟN 東経32.89972ﾟE
両都市の地表での最短距離 843km
を用いて地球を球と仮定して赤道半径Rを推定せよ。
ai=31.20194
ak=29.91611
bi=24.08889
bk=32.89972
u=pi/180
A=c(cos(ai*u)*cos(ak*u),cos(ai*u)*sin(ak*u),sin(ai*u))
B=c(cos(bi*u)*cos(bk*u),cos(bi*u)*sin(bk*u),sin(bi*u))
AB=sqrt(sum((A-B)^2))
d=843
# asin(AB/2)*2*R=d
R=d/(asin(AB/2)*2)
R
Timeline: How The U.S. Reached 200,000 Deaths From COVID-19
トランプは２月の段階で
It's also more deadly than your, you know, even your strenuous flus.
と発言して正しい認識をしたたなぁ。
ダウンロード＆関連動画＞＞
@YouTube;feature=youtu.be&t=75
１分１５秒辺りから
【広島】「うわっブスじゃー」小柄で小太りの高齢男性が女子中学生に暴言を吐く事案が発生 ★2 [potato★]
http://2chb.net/r/newsplus/1600575993/1 1 名前：potato ★[] 投稿日：2020/09/20(日) 13:26:33.55 ID:GbdyZADl9
広島県警によると、１７日午前７時ごろ、東広島市西条町大沢で女子中学生への暴言が発生しました。（実行者の特徴：高齢男性、小柄、小太り、ジーパン、頭に白色系タオル巻く）
■実行者の言動や状況
・登校途中の女子生徒に暴言を吐いた。
・「うわっブスじゃー」
■現場付近の施設
・向陽中学校、★三升原交差点、国道３７５号線
2020/9/18 22:24 (JST)
https://this.kiji.is/679679671982326881 ※前スレ
http://2chb.net/r/newsplus/1600572224/ 底辺医大卒なんかに絶対自分とか家族を任せちゃいけない
公開する羽目になるよ
>>635 シリツ医でも手先の器用なのはいるよ。
頭が器用なら底辺シリツ医大なんかにゃいかないな。
"某女子大には決して嘘をつかない女子大生と必ず嘘をつく女子大生がいることがわかっている。
この女子大の学生（嘘つきかどうかは不明）から
「あなたのいうことが正しければ手コキかフェラをしてあげる、間違っていれば何もしてあげない」と言われた。
女子大生にフェラをしてもらうには何と言えばいいか？
"
rm(list=ls())
TE=cbind(rep(0:1,c(4,4)),rep(0:3,2))
colnames(TE)=c('JD','service')
TE # JD 0:嘘つき 1:正直, service 0:何もしない 1:手コキ 2:フェラ 3:手コキ＋フェラ
cond1 <- function(P,Q) !(P&!Q) # ｐならばQ
cond2 <- function(P,Q) cond1(P,Q) & cond1(!P,!Q) # （ｐならばQ） かつ（ｐでないならQでない）
f <- function(x){
x[1]==1 & cond2(cond2(x[1]==1,x[2]!=1),x[2]>0) | x[1]==0 & !cond2(cond2(x[1]==1,x[2]!=1),x[2]>0)
}
TE[(apply(TE,1,f)),]
cond3 <- function(P,Q) P==Q
f <- function(x){
x[1]==1 & cond3(cond3(x[1]==1,x[2]!=1),x[2]>0) | x[1]==0 & !cond3(cond3(x[1]==1,x[2]!=1),x[2]>0)
}
TE[(apply(TE,1,f)),]
医者ならば、シリツ卒なら馬鹿である から
シリツ卒ならば、医者ならば馬鹿である が、導けるか？
という論理命題の問題を臨床適用ｗするとこうなる。
甲状腺癌ならば、未分化癌なら予後不良である から
未分化癌ならば、甲状腺癌なら予後不良である が、導けるか？
Rに真理表を使って解答させるスクリプトは以下の通り。
# P->(Q->R) |- Q->(P->R)
library('gtools')
pm3=permutations(2,3,v=c(T,F),re=TRUE)
colnames(pm3)=c('P','Q','R'); pm3
imply <- function(x,y) !(x&&!y)
f <- function(P,Q,R) imply(imply(P,imply(Q,R)),imply(Q,imply(P,R)))
f1 <- function(pm) f(pm[1],pm[2],pm[3])
result=logical(8)
for(i in 1:8) result[i]=f1(pm3[i,])
cbind(pm3,result)
> cbind(pm3,result)
P Q R result
[1,] FALSE FALSE FALSE TRUE
[2,] FALSE FALSE TRUE TRUE
[3,] FALSE TRUE FALSE TRUE
[4,] FALSE TRUE TRUE TRUE
[5,] TRUE FALSE FALSE TRUE
[6,] TRUE FALSE TRUE TRUE
[7,] TRUE TRUE FALSE TRUE
[8,] TRUE TRUE TRUE TRUE
医者ならば、シリツ卒なら馬鹿である から
シリツ卒ならば、医者ならば馬鹿である が、導けるか？
という論理命題の問題を臨床適用ｗするとこうなる。
甲状腺癌ならば、未分化癌なら予後不良である から
未分化癌ならば、甲状腺癌なら予後不良である が、導けるか？
'%=>%' = function(P,Q) !(P & !Q)
M=c(T,F)
R=c(T,F)
C=c(T,F)
gr=expand.grid(M,R,C)
colnames(gr)=c('M','R','C')
gr
f4 <- function(M,R,C) (M %=>% (R %=>% C)) %=>% (R %=>% (M %=>% C))
mapply(f4,gr[,1],gr[,2],gr[,3])
Windows Registry Editor Version 5.00
[HKEY_CURRENT_USER\Control Panel\Personalization\Desktop Slideshow]
"LastTickLow"=dword:00000000
"LastTickHigh"=dword:00000000
"Interval"=dword:000249f0
"Shuffle"=dword:00000001
以下の中から論理的に同値な組み合わせをすべて列挙せよ。
a : 馬鹿ならば(シリツ医ならば裏口である）
b : (馬鹿ならばシリツ医)ならば裏口である）
c : 馬鹿ならば(裏口ならばシリツ医である
d : (馬鹿ならば裏口)ならばシリツ医である
e : シリツ医ならば(馬鹿ならば裏口である)
f : (シリツ医ならば馬鹿)ならば裏口である
g : シリツ医ならば(裏口ならば馬鹿である)
h : (シリツ医ならば裏口)ならば馬鹿である)
i : 裏口ならば(馬鹿ならばシリツ医である)
j : (裏口ならば馬鹿)ならばシリツ医である
k : 裏口ならば(馬鹿ならばシリツ医である)
l : (裏口ならば馬鹿)ならばシリツ医である)
以下の中から論理的に同値な組み合わせをすべて列挙せよ。
a : 馬鹿ならば(シリツ医ならば裏口である）
b : (馬鹿ならばシリツ医)ならば裏口である）
c : 馬鹿ならば(裏口ならばシリツ医である
d : (馬鹿ならば裏口)ならばシリツ医である
e : シリツ医ならば(馬鹿ならば裏口である)
f : (シリツ医ならば馬鹿)ならば裏口である
g : シリツ医ならば(裏口ならば馬鹿である)
h : (シリツ医ならば裏口)ならば馬鹿である)
i : 裏口ならば(馬鹿ならばシリツ医である)
j : (裏口ならば馬鹿)ならばシリツ医である
k : 裏口ならば(シリツ医ならば馬鹿である)
l : (裏口ならばシリツ医)ならば馬鹿である)
過去スレから同業者や患者の本音抜粋
同業者の発言：
【ウハも】 開業医達の集い 8診 【粒も】 [無断転載禁止]
670 名前：卵の名無しさん[] 投稿日：2017/05/20(土) 11:15:40.12 ID:46exOAAP
学会で川崎の医者が発表してたら、「馬鹿が何偉そうにしゃべってる。」と思う自分が嫌になるが、
これだけは学生時代から続く反射なので止められない。
患者の発言：
【医療】医者は患者にコレを言われると、内心ものすごくムッとする★4 [無断転載禁止]
810 名前：名無しさん＠１周年[] 投稿日：2017/05/21(日) 00:11:22.04 ID:+h+2h2fq0
旧帝医卒の医者が（患者としては嫌だが）
多少偉そうにしているのはわからんでもないが
底辺私立に偉そうにされたら
そりゃ患者としてはむかつくだろw
'%=>%' = function(P,Q) !(P & !Q)
B=c(T,F)
S=c(T,F)
U=c(T,F)
gr=expand.grid(B,S,U)
colnames(gr)=c('B','S','U')
gr
f <- function(B,S,U) (B %=>% (S %=>% U)) %=>% (S %=>% (B %=>% U))
mapply(f,gr[,1],gr[,2],gr[,3])
f <- function(B,S,U) (S %=>% (B %=>% U)) %=>% (B %=>% (S %=>% U))
mapply(f,gr[,1],gr[,2],gr[,3])
f <- function(B,S,U) (B %=>% (S %=>% U)) %=>% ((B %=>% S) %=>% U)
cbind(gr,mapply(f,gr[,1],gr[,2],gr[,3]))
f <- function(B,S,U) (B %=>% (S %=>% U)) %=>% ((B %=>% S) %=>% U)
mapply(f,gr[,1],gr[,2],gr[,3])
cbind(gr,mapply(f,gr[,1],gr[,2],gr[,3]))
シリツ医 ならば (馬鹿 ならば 裏口 である) という命題が真であるときに結論できるのは以下のいずれか？
1 : シリツ医 ならば (裏口 ならば 馬鹿 である)
2 : 馬鹿 ならば (シリツ医 ならば 裏口 である)
3 : 馬鹿 ならば (裏口 ならば シリツ医 である)
4 : 裏口 ならば (シリツ医 ならば 馬鹿 である)
5 : 裏口 ならば (馬鹿 ならば シリツ医 である)
安い指輪しててもブスで金だけの医学科の彼女持ちの私立底辺医大生君は元気かな？
スマホ・出会い系アプリの垢複数持ちしてまで浮気お疲れ様。
デートも食事も可愛い子には拒否られて裏でストーカー行為しながら、相手されずモテないからって自称ヤリチンアピすることしかできない可哀想な私立底辺非モテ医大男の貴方はある意味偉大です。
Last but not least, three laws of Do-Teihen Medical School, currently called Gachi'Ura by its graduates.
1: It is not the bottom medical school but its enrollee that is despicable, which deserves to be called a bona fide moron beyond redemption.
2: The graduates of Do-Teihen are so ashamed that none of them dare to mention their own alma mater which they have gone through.
3: The Do-Teihen graduates are so ashamed of having bought their way into the exclusively bottom-leveled medical school
that they tend to call a genuine doctor a charlatan who elucidates their imbecility
私立底辺医大生ぶっさくて草
イケメンって言ってあげましょう(笑)
うすむらさき
@xxxxxx
ヤリチンはたいていブサイク。
ヤリチン公言してるやつらはまずブサメン。
すかぽんさんがツイートしました
@xxxxxxxx
ブサイクのヤリチン、一杯いるじゃん…
お釈迦様さんがツイートしました
@xxxxxxxx
ブサイクなヤリチンが世界で1番たちが悪い。ブサイクはブスしか寄ってこねーから(笑)一生ブスどもとつるんでろよ。
sim <- function(){
x=sample(52)
flg=FALSE
i=1
while(flg==FALSE & i<52){
flg <- abs(x[i]-x[i+1])==26
i=i+1
}
return(flg)
}
sim()
【コロナ】20代の感染、「第2波」で10倍…無症状者の2割が入院後に重症化 和歌山県 [ばーど★]
http://2chb.net/r/newsplus/1600896274/ source('tools.R')
prop.test(c(7,68),c(63,167))
poisson.test(c(7,68),c(63,167))
jags4prop(7,68,63,167)
# 重症化率
binom::binom.exact(11,52)
# 有症化率
binom::binom.exact(11+21,52)
Three laws of lowest-ranked medicalschool
1: It is not the lowest-ranked medical school but its enrollee that is despicable, which deserves to be called a bona fide moron beyond redemption.
2: The graduates of lowest-ranked medical school are so ashamed that none of them dare to mention their own alma mater which they have gone through.
3: The lowest-ranked medical school graduates are so ashamed of having bought their way into such schools that they tend to call a genuine doctor a charlatan who elucidates their imbecility.
>>654 話題のフォントにしてみた。
with コロナで三密を避けて生産
without コロナで三密で生産
後者の方が生産性が高いのは自明。
中国は後者の戦略で経済回復しつつあるというね。
ド底辺医大の三法則
1: It is not the lowest-ranked medical school but its enrollee that is despicable, which deserves to be called a bona fide moron beyond redemption.
ド底辺シリツ医大が悪いのではない、本人の頭が悪いんだ。
2: The graduates of lowest-ranked medical school are so ashamed that none of them dare to mention their own alma mater which they have gone through.
ド底辺シリツ医大卒は恥ずかしくて、学校名を皆さま言いません。
3: The lowest-ranked medical school graduates are so ashamed of having bought their way into such schools that they tend to call a genuine doctor a charlatan who elucidates their imbecility.
ド底辺シリツ医大卒は裏口入学の負い目から裏口馬鹿を暴く人間を偽医者扱いしたがる。
- ショートカットを表示しない
[HKEY_CURRENT_USER\Software\Microsoft\Windows\CurrentVersion\Explorer]
"link"=hex:00,00,00,00
「保守」「ナショナリスト」がナショナリズムを解体するグローバリストの安倍を礼賛する一方、パヨクは「戦後レジーム」を確定させた安倍を「戦前回帰の復古主義者」と誤認する。
>>656 東京・江戸川区にある食品加工会社の工場で、新たに従業員73人が新型コロナウイルスに感染したことが確認され、これでこの工場での感染確認は78人になりました。
会社では、24日から工場の稼働を停止し、改めて消毒作業をすることにしています。
https://www3.nhk.or.jp/news/html/20200924/k10012632831000.html こういうのが続いて日本の生産性が低下、国が衰退していくんだろうなぁ。
with コロナで三密を避けて生産
without コロナで三密で生産
後者の方が生産性が高いのは自明。
中国は後者の戦略で経済回復しつつあるという。
主語が何かすら理解していない底辺シリツ医の症例報告
これは永久保存に価する！
小学校で習うはずに主語が何かすら習得していないのに、底辺シリツ医大に入学できるとは、裏口入学以外に説明ができるだろうか？
（補足）
主語と述語って何年生で習うのか調べたらこんな動画がヒットした。
授業「主語と述語をみつけよう」｜国語｜小１・小２｜群馬県
ダウンロード＆関連動画＞＞
@YouTube シリツ医は小学校１－２年で習うことすら習得できていない。
こんな学力でどうして大学に入学できるのだろうか？裏口入学以外に説明できる人がいたら御教授を賜りたい。
二 〇 一 四 年 の 世界 経済 フォーラム 年次 会議（ ダボス 会議） の 冒頭 演説 で 安倍 は、 徹底的 に 日本 の 権益 を 破壊 する と 宣言。 電力 市場 の 完全 自由化、 医療 の 産業 化、 コメ の 減反 の 廃止、 法人 税率 の 引き下げ、 雇用 市場 の 改革、 外国人 労働者 の 受け入れ、 会社法 の 改正 などを 並べ立て、「 その とき 社会 は あたかも リセット・ボタン を 押し た よう に なっ て、 日本 の 景色 は 一変 する でしょ う」 と 言い放っ た。
適菜収. 国賊論 (Kindle の位置No.248-252). ＫＫベストセラーズ. Kindle 版.
「保守」「ナショナリスト」がナショナリズムを解体するグローバリストの安倍を礼賛する一方、頭の悪い一部の左翼は「戦後レジーム」を確定させた安倍を「戦前回帰の復古主義者」と誤認する。自分の世界観に合わせて、都合よく現実を解釈するわけだ。
移民は「外国人材」、家族制度の破壊は「女性の活用」、戦争に巻き込まれることは「積極的平和主義」、秩序破壊のための実験は「国家戦略特区」、不平等条約のＴＰＰは「国家百年の計」、南スーダンの戦闘は「衝突」、米軍機の墜落は「不時着」……。
> 巷 には、 少子 高齢 化 を 迎える 日本 において は、 デフレ は 避け られ ない という 議論 も あり ます が、 これ は 誤り です。 実際 に 多く の 国 は、 人口 が 減少 し て い ても、 デフレ には 陥っ て い ませ ん。
(中略)
> 一方 で、 デフレ から 脱却 する ため には、 金融政策 と 同時に 財政政策 も 必要 と 考え て い ます。 国民 の 命 や 子ども たち の 安全 を 守る ため の 投資、 地域 が 生産性 を 高め、 競争 力 を 得る ため の 未来 への 投資 は 行う べき だ と 考え ます。
>ただ、 残念 ながら、 税率 を 上げる こと イコール 税収 が 増え て いく こと にはなり ませ ん。 一 九九 七年 に 消費税 を 三 パーセント から 五 パーセント に 上げ た とき は、 五十 四 兆 円 だっ た 税収 は、 翌 年度 は 四十 九 兆 円 に 減少 し、 それ 以降、 五十 四 兆 円 に 到達 し た こと は 一度 も ない。
安倍 晋三. 新しい国へ 美しい国へ 完全版
権力 の 分散 を 唱える のが 保守 で あり、 権力 の 集中 を 唱える のが 左翼 で ある。 理由 は 簡単 で、 保守 は 人間 理性 を 信用 し ない が、 左翼 は 合理的 かつ 理性的 で ある から だ。
裏口でなくて、学力考査で大学入れたなら、これくらいは答えられるだろ？
問題：
シリツ医 ならば (馬鹿 ならば 裏口 である) という命題が真であるときに結論できるのは以下のいずれか？
1 : シリツ医 ならば (裏口 ならば 馬鹿 である)
2 : 馬鹿 ならば (シリツ医 ならば 裏口 である)
3 : 馬鹿 ならば (裏口 ならば シリツ医 である)
4 : 裏口 ならば (シリツ医 ならば 馬鹿 である)
5 : 裏口 ならば (馬鹿 ならば シリツ医 である)
裏 医 問 嘘 「 と フ 子 嘘 「 と チ
口 師 題 を あ 言 ェ 供 を あ 言 ョ
馬 免 は つ な わ ラ 向 つ な わ コ
鹿 許 こ か た れ を き か た れ を
で も れ な の た し は な の た も
な っ い い ｡ て こ い い ｡ ら
い て 若 う も っ お う う
証 い い こ ら ち 菓 こ に
明 な 女 と う 子 と は
に い 医 が に 屋 が 何
サ 小 か 正 は か 正 と
ク 学 ら し 何 ら し 言
ッ 生 け と け え
と で れ 言 れ ば
答 も ば え ば い
え 正 手 ば チ い
た 解 コ い ョ か
ら す キ い コ ？
？ る か か か
ぞ フ ？ 飴
｡ ェ を
ラ あ
を げ
し る
て 」
あ
げ
る
」
１ 底
： 辺
ド 医
底 大
辺 の
シ 三
リ 法
ツ 則
医
大
が
悪
い
の
で
は
な
い
､
本
人
の
頭
が
悪
い
ん
だ
｡
裏 ド 底
口 底 辺
馬 辺 医
鹿 シ 大
を リ の
暴 ツ 第
く 医 三
人 大 法
間 卒 則
を は
偽 裏
医 口
者 入
扱 学
い の
し 負
た い
が 目
る か
｡ ら
ｒｍ（ｌｉｓｔ＝ｌｓ（））
ｘ＝”
東京医大の事件は裏口入学が現在進行形であること如実にしめした事件だよね。
しりつ医の使命は裏口入学撲滅国民運動の先頭に立つことだよ。
裏口入学の学生を除籍処分にしないかぎり、信頼の回復はないね。つまり、いつまで経ってもしりつ医大卒＝裏口ばかと汚名は拭えない。しりつ出身者こそ、裏口入学に厳しい処分せよを訴えるべき。
裏口入学医師の免許剥奪を！の国民運動の先頭に立てばよいぞ。
僕も裏口入学とか、言ってたら信頼の回復はない。
”
ｆ ＜－ ｆｕｎｃｔｉｏｎ（ｘ，ｓ＝２）｛
ｎ＝ｎｃｈａｒ（ｘ）
ｙ＝ＮＵＬＬ
ｆｏｒ（ｉ ｉｎ １：ｎ）｛
ｙ ＜－ ｐａｓｔｅ０（ｙ，ｓｕｂｓｔｒ（ｘ，ｉ，ｉ），ｐａｓｔｅ０（ｒｅｐ（’ ’，ｓａｍｐｌｅ（０：ｓ，１）），ｃｏｌｌａｐｓｅ＝’’））
｝
ｃａｔ（ｙ）
ｉｎｖｉｓｉｂｌｅ（ｙ）
｝
ｆ（ｘ）
さ て は シ リ ツ だ な 。
そ う い う の い い か ら サ ク っと正 解 し て み ！
こ れ に 即 答 が つ け ば即 、 終 わ っ たの に。
問 題は こ れ
嘘 をつ か な い 若 い女医 か ら
「あな た の い うこ と が 正 し け れば 手コ キかフ ェ ラ を し て あ げ る 」 と言わ れた 。
フ ェ ラ を し ても ら う に は 何 と言 え ばい い か ？
大 本 シ 学 鹿 扱
ド 卒 校 ん
が 人 リ の を い
底 は 名 。
悪 の ツ 負 暴 し
辺 ド 恥 を
ド い 頭 医 い く た
医 底 ず 皆
底 の が 大 目 人 が
大 辺 か さ
辺 で 悪 卒 か 間 る
の シ し ま
シ は い は ら を 。
三 リ く 言
リ な ん ド 裏 裏 偽
法 ツ て い
ツ い だ 底 口 口 医
則 医 、 ま
医 、 。 辺 入 馬 者
大 学 せ
扱 鹿 学 シ 本 大
ん 校 卒 ド
い を の リ 人 が
。 名 は 底
し 暴 負 ツ の 悪
を 恥 ド 辺
た く い 医 頭 い ド
皆 ず 底 医
が 人 目 大 が の 底
さ か 辺 大
る 間 か 卒 悪 で 辺
ま し シ の
。 を ら は い は シ
言 く リ 三
偽 裏 裏 ド ん な リ
い て ツ 法
医 口 口 底 だ い ツ
ま 、 医 則
者 馬 入 辺 。 、 医
せ 学 大
時 差 と は 識 払 バ か は 向 年 底 し で は わ
不 代 別 い 誰 的 っ カ っ 一 か 代 辺 て 軽 面 な
朽 に 感 う も に て だ て 人 っ の 医 る 蔑 と い
の 大 が イ 受 考 、 の 好 も て 人 卒 ん し 向 け
名 学 凄 メ 験 え し 裏 き い は 間 を だ 、 か ど
投 受 く ー し て か 口 好 ま 言 は 今 、 嘲 っ ね
稿 験 、 ジ よ 、 も だ ん せ わ 、 で こ 笑 て 。
を し 特 で う 数 同 の で ん な お も の し は
引 た 殊 開 と 千 業 と ド で い そ 「 裏 て 絶
用 け 民 業 す 万 者 散 底 し け ら 何 口 い 対
再 ど の 医 ら と か 々 辺 た れ く 偉 バ る に
掲 、 た の し い ら 罵 医 。 ど は そ カ よ そ
昔 め バ な う も ら に 本 、 ８ う が 。 ん
私 は の カ か 法 患 れ 行 人 俺 － な 」 当 な
は 今 特 息 っ 外 者 る く に く ９ こ と の こ
昭 よ 殊 子 た な か の 同 は ら 割 と 心 本 と
和 り 学 以 。 金 ら を 級 面 い は 抜 の 人 は
の も 校 外 常 を も わ 生 と の ド か 底 に 言
わ は で し 底 年 向 は か バ 払 識 は と 差 時
な 面 軽 て 辺 代 か 一 っ カ っ 的 誰 い 別 代 不
い と 蔑 る 医 の っ 人 て だ て に も う 感 に 朽
け 向 し ん 卒 人 て も 好 の 、 考 受 イ が 大 の
ど か 、 だ を 間 は い き 裏 し え 験 メ 凄 学 名
ね っ 嘲 、 今 は 言 ま 好 口 か て し ー く 受 投
。 て 笑 こ で 、 わ せ ん だ も 、 よ ジ 、 験 稿
は し の も お な ん で の 同 数 う で 特 し を
絶 て 裏 「 そ い で ド と 業 千 と 開 殊 た 引
対 い 口 何 ら け し 底 散 者 万 す 業 民 け 用
に る バ 偉 く れ た 辺 々 か と ら 医 の ど 再
そ よ カ そ は ど 。 医 罵 ら い し の た 、 掲
ん 。 が う ８ 、 本 に ら も う な バ め 昔
な 当 」 な － 俺 人 行 れ 患 法 か カ の は 私
こ の と こ ９ く に く る 者 外 っ 息 特 今 は
と 本 心 と 割 ら は 同 の か な た 子 殊 よ 昭
は 人 の 抜 は い 面 級 を ら 金 。 以 学 り 和
言 に 底 か ド の と 生 わ も を 常 外 校 も の
＃ ｓｔｒ －＞ ｍａｔｒｉｘ（ｔａｔｅ）
ｔａｔｅ ＜－ ｆｕｎｃｔｉｏｎ（ｓｔｒ，ｍｏｊｉ＝ＮＵＬＬ）｛ ＃ ｓｔｒ：文字列， ｍｏｊｉ：１列の文字数
ｘ＝ｇｓｕｂ（’￥ｎ’，’’，ｓｔｒ）
ｎ＝ｎｃｈａｒ（ｘ）
ｍ＝ｉｆｅｌｓｅ（ｉｓ．ｎｕｌｌ（ｍｏｊｉ），ｃｅｉｌｉｎｇ（ｓｑｒｔ（ｎ）），ｍｏｊｉ）
ａｄｄ＝ｍ＾２－ｎ
ｙ＝ｐａｓｔｅ０（ｘ，ｐａｓｔｅ０（ｒｅｐ（’ ’，ａｄｄ），ｃｏｌｌａｐｓｅ＝’’））
Ｙ＝ＮＵＬＬ
ｆｏｒ（ｉ ｉｎ １：ｍ＾２） Ｙ［ｉ］＝ｓｕｂｓｔｒ（ｙ，ｉ，ｉ）
Ｌ＝Ｒ＝ｍａｔｒｉｘ（Ｙ，ｍ，ｍ）
ｆｏｒ（ｉ ｉｎ １：ｍ） ｃａｔ（Ｌ［ｉ，］，’￥ｎ’）＃ 左から開始
ｆｏｒ（ｉ ｉｎ １：ｍ） Ｒ［，ｍ＋１－ｉ］＝Ｌ［，ｉ］ ＃
ｃａｔ（’￥ｎ￥ｎ’）
ｆｏｒ（ｉ ｉｎ １：ｍ） ｃａｔ（Ｒ［ｉ，］，’￥ｎ’）＃ 右から開始
｝
ｓｔｒ＝”
はなのいろは
うつりにけりな
いたずらに
わがみよにふる
ながめせしまに ”
ｎｃｈａｒ（ｓｔｒ）
ｘ＝ｇｓｕｂ（’￥ｎ’，’’，ｓｔｒ）
ｎｃｈａｒ（ｘ）
ｔａｔｅ（ｓｔｒ，１１）
> str="
+ はなのいろは
+ うつりにけりな
+ いたずらに
+ わがみよにふる
+ ながめせしまに "
> tate(str,11)
は わ な
な が が
の う み め
い つ よ せ
ろ り に し
は に い ふ ま
け た る に
り ず
な ら
に
な わ は
が が な
め み う の
せ よ つ い
し に り ろ
ま ふ い に は
に る た け
ず り
ら な
に
(sqrt(1+x)-sqrt(1+x^2))/(sqrt(1-x^2)-sqrt(1-x))
(sqrt(1+x)-sqrt(1+x^2))/(sqrt(1-x^2)-sqrt(1-x))
100日で崩壊する政権 コロナ禍日本、安倍政権の軌跡 (日本語)
思わず注文してしまった。
100日で崩壊する政権 コロナ禍日本、安倍政権の軌跡 (日本語)
を注文してした。
Kindle版もあったけど、家族にも読ませたいので紙の方にした。
東京女子医大、学費1200万円値上げ コロナで経営難 9/27(日) 21:00配信
私立大学の医学部で学費を値上げする動きが出ている。
東京女子医科大は2021年度の入学生について6年間で計1200万円上げる。
コロナ禍による大学病院の経営悪化の影響などが指摘されている。
東京女子医大がホームページで公開している入学案内によると、
6年間の学費は4621万4千円。
広報担当者によると年間200万円の施設設備費の項目が新たに加わったという。
値上げの詳しい理由はホームページでは示しておらず、取材にも回答していない。
河合塾が私立大医学部の20年度の募集要項などをまとめたところ、
主な選抜方式で総額が最も高いのは川崎医科大（岡山県）の4736万5千円。
今回の値上げで東京女子医大は21年度から、
金沢医科大（石川県）を上回り2番目に高いところになりそうだ。
>>685 そんなオマエは反日ド底辺の風邪風邪クルクルパー
医学的に入れないオマエの低脳さがそんなに悔しいのかいＷ
１ ２
表表 見たのが表1
表裏 見たのが表1
裏表 見たのが裏1
裏裏 見たのが裏1
表表 見たのが表2
表裏 見たのが裏2
裏表 見たのが表2
裏裏 見たのが裏2
# y=tan(A)(x-a1)+a2
# y=tan(B)(x-b1)+b2
koten <- function(a1,a2,a,b1,b2,b){
A=a*pi/180
B=b*pi/180
x = (a1* tan(A) - a2 - b1 *tan(B) + b2)/(tan(A) - tan(B))
y = (a1* tan(A)* tan(B) - b1 *tan(A)* tan(B) + b2 *tan(A) - a2* tan(B))/(tan(A) - tan(B))
c(x,y)
}
koten(0,0,60,1,0,120)
# y=tan(A)(x-a1)+a2 ,y=tan(B)(x-b1)+b2
koten <- function(a1,a2,a,b1,b2,b){
A=a*pi/180
B=b*pi/180
x = (a1* tan(A) - a2 - b1 *tan(B) + b2)/(tan(A) - tan(B))
y = (a1* tan(A)* tan(B) - b1 *tan(A)* tan(B) + b2 *tan(A) - a2* tan(B))/(tan(A) - tan(B))
c(x,y)
}
# coordinates -> angle BAC
BAC <- function(B,A,C){
if(is.complex(B)|is.complex(A)|is.complex(C)){
a=c(Re(A),Im(A)); b=c(Re(B),Im(B)); c=c(Re(C),Im(C))
}else{a=A;b=B;c=C}
ab=b-a
ac=c-a
dot=sum(ab*ac)
bac=acos(dot/sqrt(sum(ab^2))/sqrt(sum(ac^2)))
return(c(rad=bac,deg=bac*180/pi))
}
c=koten(0,0,9, 1,0,180-75)
d=koten(0,0,3, 1,0,180-51)
B=1+0i
C=c[1]+1i*c[2]
D=d[1]+1i*d[2]
BAC(D,C,B)
内視鏡の待機時間の暇つぶし
# y=tan(A)(x-a1)+a2 ,y=tan(B)(x-b1)+b2
koten <- function(a1,a2,a,b1,b2,b){
A=a*pi/180
B=b*pi/180
x = (a1* tan(A) - a2 - b1 *tan(B) + b2)/(tan(A) - tan(B))
y = (a1* tan(A)* tan(B) - b1 *tan(A)* tan(B) + b2 *tan(A) - a2* tan(B))/(tan(A) - tan(B))
c(x,y)
}
# coordinates -> angle BAC
BAC <- function(B,A,C){
if(is.complex(B)|is.complex(A)|is.complex(C)){
a=c(Re(A),Im(A)); b=c(Re(B),Im(B)); c=c(Re(C),Im(C))
}else{a=A;b=B;c=C}
ab=b-a
ac=c-a
dot=sum(ab*ac)
bac=acos(dot/sqrt(sum(ab^2))/sqrt(sum(ac^2)))
return(c(rad=bac,deg=bac*180/pi))
}
c=koten(0,0,9, 1,0,180-75)
d=koten(0,0,3, 1,0,180-51)
B=1+0i
C=c[1]+1i*c[2]
D=d[1]+1i*d[2]
BAC(D,C,B)
ド底辺シリツ医の三法則
一、ド底辺シリツ医大が悪いのではない、本人の頭が悪いんだ。
二、ド底辺シリツ医大卒は恥ずかしくて、学校名を皆さま言いません。
三、ド底辺シリツ医大卒は裏口入学の負い目から裏口馬鹿を暴く人間を偽医者扱いしたがる。
> naname()
底 リ 三 、 ツ で 頭 、 は を 、 入 く
ド シ の 一 リ の の 二 卒 名 三 口 暴
辺 医 シ い 人 大 校 裏 を 。
ツ 則 辺 悪 本 。 医 学 。 は 鹿 る
法 底 が 、 だ ツ 、 ん 卒 馬 が
ド 大 い ん リ て せ 大 口 た
医 な い シ く ま 医 裏 し
は 悪 辺 し い ツ ら い
が 底 か 言 リ か 扱
ド ず ま シ 目 者
恥 さ 辺 い 医
皆 底 負 偽
ド の を
学 間
ド 辺 ツ 法 ド 医 は が ド 恥 皆 ド 学 人
底 シ 医 則 底 大 な 悪 底 ず さ 底 の 間
リ の 辺 が い い 辺 か ま 辺 負 を
三 一 シ 悪 、 ん シ し 言 シ い 偽
、 リ い 本 だ リ く い リ 目 医
ツ の 人 。 ツ て ま ツ か 者
で の 医 、 せ 医 ら 扱
頭 二 大 学 ん 大 裏 い
、 卒 校 。 卒 口 し
は 名 は 馬 た
を 三 裏 鹿 が
、 口 を る
入 暴 。
く
一
、
ド
底
辺
シ
リ
ツ
医
大
が
悪
い
の
で
は
な
い
、
本
人
の
頭
が
悪
い
ん
だ
。
二
、
ド
底
辺
シ
リ
ツ
医
大
卒
は
恥
ず
か
し
く
て
、
学
校
名
を
皆
さ
ま
言
い
ま
せ
ん
。
三
、
ド
底
辺
シ
リ
ツ
医
大
卒
は
裏
口
入
学
の
負
い
目
か
ら
裏
口
馬
鹿
を
暴
く
人
間
を
偽
医
者
扱
い
し
た
が
る
。
つづら折り、斜め読み
一 辺 シ の で ん だ ず か 、 ド を 暴 。
、 底 リ い は い 。 恥 し 三 底 鹿 く
ド ツ 悪 な 悪 は く 辺 馬 人
医 が い が 二 卒 て 。 シ 口 間
大 、 頭 、 大 、 ん リ 裏 を
本 の ド 医 学 せ ツ ら 偽
人 底 ツ 校 ま 医 か 医
辺 リ 名 い 大 目 者
シ を 言 卒 い 扱
皆 ま は 負 い
さ 裏 の し
口 学 た
入 が
る
。
一 辺 シ の で ん だ ず か 、 ド を 暴 。
、 底 リ い は い 。 恥 し 三 底 鹿 く
ド ツ 悪 な 悪 は く 辺 馬 人
医 が い が 二 卒 て 。 シ 口 間
大 、 頭 、 大 、 ん リ 裏 を
本 の ド 医 学 せ ツ ら 偽
人 底 ツ 校 ま 医 か 医
辺 リ 名 い 大 目 者
シ を 言 卒 い 扱
皆 ま は 負 い
さ 裏 の し
口 学 た
入 が
る
。
> str="安倍は二回も仮病で逃亡した国賊"
> naname2(str)
安 は も 逃 賊
倍 回 で 国
二 病 た
仮 し
亡
安 倍 二 仮 亡
は 回 病 し
も で た
逃 国
賊
安 倍 も 仮 賊
は 回 病 国
二 で た
逃 し
亡
安 は 二 逃 亡
倍 回 で し
も 病 た
仮 国
賊
＃ １行斜め読み
ｎａｎａｍｅ ＜－ ｆｕｎｃｔｉｏｎ（
ｘ＝”さては裏口容疑者のしりつ医だな”，ｒｅｖｅｒｓｅ＝ＴＲＵＥ
）｛
ｓｔｒ＝ｐａｓｔｅ０（’ ’，ｘ，ｃｏｌｌａｐｓｅ＝’’）
ｎ＝ｎｃｈａｒ（ｓｔｒ）
ｉｆ（ｒｅｖｅｒｓｅ）
ｆｏｒ（ｉ ｉｎ １：ｎ） ｃａｔ（ｒｅｐ（’ ’，ｎ－ｉ＋１，）， ｓｕｂｓｔｒ（ｓｔｒ，ｉ，ｉ），’￥ｎ’）
ｅｌｓｅ
ｆｏｒ（ｉ ｉｎ １：ｎ） ｃａｔ（ｒｅｐ（’ ’，ｉ－１），ｓｕｂｓｔｒ（ｓｔｒ，ｉ，ｉ）， ’￥ｎ’）
｝
ｎａｎａｍｅ（）
＞ ｎａｎａｍｅ（）
さ
て
は
裏
口
容
疑
者
の
し
り
つ
医
だ
な
ｎａｎａｍｅ３ ＜－ ｆｕｎｃｔｉｏｎ（
ｓｔｒ＝”ど底辺しりつ医大卒は裏口入学の負い目から裏口馬鹿を暴く人間を偽医者扱いしたがる”，
ｎ＝１５）｛
ｘ＝ｃｈａｒａｃｔｅｒ（）
ｆｏｒ（ｉ ｉｎ １：ｎｃｈａｒ（ｓｔｒ）） ｘ［ｉ］＝ｓｕｂｓｔｒ（ｓｔｒ，ｉ，ｉ）
ｓ＝ｍａｔｒｉｘ（ｒｅｐ（’ ’，ｎ＾２），ｎ）
ｆｏｒ（ｉ ｉｎ １：ｎ） ｓ［ｉ，ｎ－ｉ＋１］ ＜－ ｘ［ｉ］
ｆｏｒ（ｉ ｉｎ １：（ｎ－１）） ｓ［ｉ＋１，ｎ－ｉ＋１］＝’ ’
ｆｏｒ（ｉ ｉｎ （ｎ＋１）：（ｎ＋ｎ－２）） ｓ［ｉ－ ｎ＋２ ， ２＊ｎ－ｉ＋１］ ＜－ ｘ［ｉ］
ｆｏｒ（ｉ ｉｎ １：（ｎ－３）） ｓ［ｉ＋３，ｎ－ｉ＋１］＝’ ’
ｆｏｒ（ｉ ｉｎ （２＊ｎ－１）：（２＊ｎ－１＋ｎ－５）） ｓ［ｉ－２＊ｎ＋６ ， ３＊ｎ－ｉ－１］ ＜－ ｘ［ｉ］
ｆｏｒ（ｉ ｉｎ １：（ｎ－５）） ｓ［ｉ＋５，ｎ－ｉ＋１］＝’ ’
ｆｏｒ（ｉ ｉｎ （３＊ｎ－５）：（３＊ｎ－５＋ｎ－７）） ｓ［ｉ－３＊ｎ＋１２， ４＊ｎ－ｉ－５］ ＜－ ｘ［ｉ］
ｆｏｒ（ｉ ｉｎ １：ｎ） ｃａｔ（ｎａ．ｏｍｉｔ（ｓ［ｉ，］），’￥ｎ’）
｝
ｎａｎａｍｅ３（）
ド
底
辺 負
シ い
リ 目 間
ツ か を
医 ら 偽
大 裏 医
卒 口 者
は 馬 扱
裏 鹿 い
口 を し
入 暴 た
学 く が
の 人 る
ド
底 の
辺 負
シ い 人
リ 目 間
ツ か を る
医 ら 偽
大 裏 医
卒 口 者
は 馬 扱
裏 鹿 い
口 を し
入 暴 た
学 く が
ド
底 馬
辺 鹿
シ を
リ 暴
ツ く
医 人
大 間
卒 を
は 偽
裏 医
口 者
入 扱
学 い
の し
負 た
い が
目 る
か
ら
裏
東
京 た
医 事
大 件 頭
の だ に
事 よ 立 か
件 ね つ ぎ
は 。 こ り
裏 と 、
口 シ だ 信
入 リ よ 頼
学 ツ 。 の
が 医 回
現 の 裏 復
在 使 口 は
進 命 入 な
行 は 学 い
形 裏 の ね
で 口 学 。
あ 入 生
る 学 を
こ 撲 除
と 滅 籍
如 国 処
実 民 分
に 運 に
し 動 し
め の な
し 先 い
つ
ま な
り い
、 。 べ
い シ き
つ リ 。 立
ま ツ て
で 出 裏 ば
経 身 口 よ
っ 者 入 い
て こ 学 ぞ
も そ 医 。
シ 、 師
リ 裏 の 僕
ツ 口 免 も
医 入 許 裏
大 学 剥 口
卒 に 奪 入
＝ 厳 を 学
裏 し ！ と
口 い の か
バ 処 国 、
カ 分 民 言
と せ 運 っ
汚 よ 動 て
名 を の た
は 訴 先 ら
拭 え 頭 信
え る に 頼
つ
ま 。
り
、 シ
い リ 裏
つ ツ 口 。
ま 出 入
で 身 学 僕
経 者 医 も
っ こ 師 裏
て そ の 口
も 、 免 入
シ 裏 許 学
リ 口 剥 と
ツ 入 奪 か
医 学 を 、
大 に ！ 言
卒 厳 の っ
＝ し 国 て
裏 い 民 た
口 処 運 ら
バ 分 動 信
カ せ の 頼
と よ 先 の
汚 を 頭 回
名 訴 に 復
は え 立 は
拭 る て な
え べ ば い
な き よ 。
い 。 い
ド シ 三 底 い が リ 名 シ 馬
底 リ 法 辺 の 悪 ツ を リ 鹿
辺 ツ 則 シ で い 医 皆 ツ を
医 リ は ん 大 さ 医 暴
の 一 ツ な だ 卒 ま 大 く
、 医 い 。 は 言 卒 人
ド 大 、 恥 い は 間
が 本 二 ず ま 裏 を
悪 人 、 か せ 口 偽
の ド し ん 入 医
頭 底 く 。 学 者
辺 て の 扱
シ 、 三 負 い
学 、 い し
校 ド 目 た
底 か が
辺 ら る
裏 。
口
ド シ 三 底 い が リ 名 シ 馬
底 リ 法 辺 の 悪 ツ を リ 鹿
辺 ツ 則 シ で い 医 皆 ツ を
医 リ は ん 大 さ 医 暴
の 一 ツ な だ 卒 ま 大 く
、 医 い 。 は 言 卒 人
ド 大 、 恥 い は 間
が 本 二 ず ま 裏 を
悪 人 、 か せ 口 偽
の ド し ん 入 医
頭 底 く 。 学 者
辺 て の 扱
シ 、 三 負 い
学 、 い し
校 ド 目 た
底 か が
辺 ら る
裏 。
口
左 上 白 な プ て は に
の が っ ロ み い く
空 無 て グ た え い
駄 い ラ 。 角 。
に た ム に
の を 省 文
で 改 ス 字
良 ペ が
し ー 並
ス ぶ
と と
読
み
左 空 に で し と み
の 駄 の 良 ス 読
上 無 た 改 ー と
が い を ペ ぶ
白 て ム ス 並
っ ラ 省 が
な グ 字
ロ 。 文
プ た に
み 角
て え
い 。
は い
く
に
左 駄 プ た に
上 に ロ 。 文
の な グ 字
空 っ ラ 省 が
白 て ム ス 並
が い を ペ ぶ
無 た 改 ー と
の 良 ス 読
で し と み
て は に
み い く
え い
角 。
医 底 で だ 恥 せ 学 い
ド の 辺 は 。 ず ん の し
底 三 シ な か 。 負 た
辺 法 リ い 二 し い が
シ 則 ツ 、 、 く 三 目 る
リ 医 本 ド て 、 か 。
ツ 一 大 人 底 、 ド ら
、 が の 辺 学 底 裏
ド 悪 頭 シ 校 辺 口
い が リ 名 シ 馬
の 悪 ツ を リ 鹿
い 医 皆 ツ を
ん 大 さ 医 暴
卒 ま 大 く
は 言 卒 人
い は 間
ま 裏 を
口 偽
入 医
者
扱
ツ ド の ん は ま 入 扱
リ 、 い い 卒 い 口 者
シ 一 悪 悪 大 言 裏 医
辺 が が 医 ま は 偽
底 則 大 頭 ツ さ 卒 を
ド 法 医 の リ 皆 大 間
三 ツ 人 シ を 医 人
の リ 本 辺 名 ツ く
医 シ 、 底 校 リ 暴
辺 い ド 学 シ を
底 な 、 、 辺 鹿
は 二 て 底 馬
で く ド 口
。 し 、 裏
だ か 三 ら
ず か
恥 。 目
ん い 。
せ 負 る
の が
学 た
し
い
東京医大の事件は裏口入学が現在進行形であること如実にしめした事件だ。
シリツ医の使命は裏口入学撲滅国民運動の先頭に立つこと。
裏口入学の学生を除籍処分にしないかぎり、信頼の回復はない。
つまり、いつまで経ってもシリツ医大卒＝裏口バカと汚名は拭えない。
シリツ出身者こそ、裏口入学に厳しい処分せよを訴えるべき。
裏口入学医師の免許剥奪を！の国民運動の先頭に立てばよい。
僕も裏口入学とか、言ってたら信頼の回復はない。
東 進 行 の 使 除 籍 ＝ 裏 医 師
京 在 形 医 命 を 処 卒 口 学 の 。
医 現 で ツ は 生 分 大 バ 入 免 い
大 が あ リ 裏 学 に 医 カ 口 許 な
の 学 る シ 口 の し ツ と 裏 剥 は
事 入 こ 入 学 な リ 汚 奪 復
件 口 と 。 学 入 い シ 名 。 を 回
裏 如 だ 撲 口 か も は き ！ の
は 実 件 滅 裏 ぎ て 拭 べ の 頼
に 事 国 り っ え る 国 信
し た 民 。 、 経 な え 民 ら
し 運 と 信 で い 訴 運 た
め 動 こ 頼 ま 。 を 動 て
の つ の つ よ の っ
先 立 回 い シ せ 先 言
に 復 、 リ 分 頭 、
頭 は り ツ 処 に か
な ま 出 い 立 と
い つ 身 し て 学
者 厳 ば 入
。 こ に よ 口
そ 学 い
、 入 。
口
裏 僕
も
裏
生活圏を超える人の移動は、確実に接触率を上げ、これが実効再生産数を挙げて、感染者数上昇を引き起こす。
現在、GOTOで東京のウィルスを全国に拡散中。
しばらくは、旅行を楽しむような若者や元気な人が隠れ陽性となり、感染者数は急には増えないが、やがてこれらが顕在化して爆発する。
世の中には、接客業を繁盛させることが「経済を回す」ことだと勘違いしてる馬鹿が多いので、
製造業がかなり疲弊していることが軽視されている。
景気が良くても派遣業者とかいう奴隷商人に賃金ピンはねされ
景気が悪くなれば真っ先にくびになる
そんな制度を作ったのが自民党
考え無しに投票した国民による意思だから喜んで解雇されれば良い
SAW VI
Did you know that in the Far East,
people pay their doctors
when they're healthy?
When they're sick,
they don't have to pay them.
So, basically,
they end up paying for what they want,
not what they don't want.
We got it all ass-backwards here.
記者 「10年間くらい(消費税)引き上げなくてもいいという、その根拠ついては何だと考えられているのか」
菅 「まさに、アベノミクスを推進をし、経済を成長させる。まさに、経済成長…え…経済を再生させると、させなければ、財政健全化ないという、その政策のである」
https://twitter.com/shin19infinity/status/1304367586738487297
アベちゃん以上にひどいじゃないか。完全に耄碌ジジイ。
安倍のほうがマシだったという時代が来そうだな。
https://twitter.com/5chan_nel (5ch newer account) D ア は 知 い も 医 は 現
S ス 削 識 い な 師 こ が
M ペ 除 を ぞ い に れ 、
- ル さ ア 。 真 最 ！ さ
I ガ れ ッ 理 も て
V ー た プ ア も イ は
で 症 こ デ ッ あ ン 裏 シ
候 と ー プ る パ 口 リ
群 く ト デ 。 ク シ ツ
ら し ー ト リ だ
い た ト （ が ツ な
方 す 例 あ 医
が る ） る で
必 レ こ あ
要 日 ッ の る
本 テ マ 。
の ル イ
貼 ル
り ド
な
表
そ 返 W タ て だ
う る O ー い な
い の R を る
う は D ス っ
レ N フ ル て
ス G ィ ー こ
が ル し と
そ 返 W タ て だ
う る O ー い な
い の R を る
う は D ス っ
レ N フ ル て
ス G ィ ー こ
が ル し と
ま グ の 種
あ ラ 練 の
、 ミ 習 道
プ ン で 楽
ロ グ 一
二〇 一一 年三 月 の 東日本大震災 と 東京 電力 福島第一原発事故 以降 にでも、
政府 による 圧倒的 な 産業 支援 や、 または 税制 優遇 を通じて 蓄電池 や それ にまつわる 半導体、 太陽光 パネル と それ に 関連 する 薄膜 技術、 あるいは ＥＶ を 想定 し た モーター と 電磁石 などの 技術 開発 に 投資 が 向かっ て いれ ば、 この 分野 で 日本 が 世界的 に 覇権 を 握る こと が 可能 で あっ た だろ う。
「戦わ ず し て 負ける 国」 という 文脈 で この 事象 を 見れ ば、 原発 依存 の 継続 は、 米国 が 仕組ん だ 日本 の「 経済的 武装解除」 だっ た のでは ない かと 私 は 推察 する。
二 一 世紀 の エネルギー 覇権 を 日本 が 握る こと は、 米国 にとって 許さ れ ない。 だから「 原発」 という 過去 の 負 の 遺産 を 背負わ せ 続ける。
そうして 世界 経済 の 中 で 戦える 武器 を 奪い取り、 経済的 属国 化 を 維持、 継続 しよ う と し た のでは ない か。
田崎基. 令和日本の敗戦 ──虚構の経済と蹂躙の政治を暴く (ちくま新書) (Kindle の位置No.2160-2164). 筑摩書房. Kindle 版.
A(t)=
at when 0<t<2400/a
2400 - a(t-2400/a)=4800-at when 2400/a<t<4800/a
B(t)=
2400 - bt when 0<t<2400/b
bt-2400 when 2400/b<t<4800/b
Aを原点して太郎君の速度をa,次郎君の速度をbとして
時刻tにおける太郎君の位置A(t)は
A(t)=
at when 0<t<2400/a
2400 - a(t-2400/a)=4800-at when 2400/a<t<4800/a
時刻tにおける太郎君の位置B(t)は
B(t)=
2400 - bt when 0<t<2400/b
bt-2400 when 2400/b<t<4800/b
一回目に出会う時刻をt1、その座標をx1として
x1=at1=2400-bt1
二回目に出会う時刻をt2、その座標をx2として
x2=4800-at2=bt2-2400
x1-x2=320なので
at1-(4800-at2)=320
at1-(bt2-2400)=320
2400-bt1-(4800-at2)=320
整理すると
at1+at2=5120
at1-bt2=-2080
at2-bt1=320-2400-4800
同時に出発してAとBの間を往復します。
ＡからＢへ向かって太郎君が，ＢからＡへ向かって次郎君が進みます。
ＡとＢ地点の間の距離は２４００メートルです。２回目に出会った地点は１回目に出会った地点よりも３２０メートルＡ側にずれた地点でした。このとき太郎と次郎の速さの比を答えなさい。
太郎君の速度をa,次郎君の速度をbとして
横軸に時間、縦軸にAからの距離をグラフにすると
黒が太郎、赤が次郎。交点の縦座標の差が320になる。
1st encounter
y=ax
y=2400-bx
を解いて
時間2400/(a+b)に2400a/(a+b))で1回の出会い
y=4800-ax
y=bx-2400
を解いて
時間7200/(a+b)に4800-7200a/(a+b))で2回目の出会い
Aからの距離の差が320ｍなので
2400a/(a+b) - ( 4800-7200a/(a+b) ) = 320
これを展開すると
7a=8b
a/b=8/7
太郎：次郎＝8：7
>>734 グラフに説明をいれてみた
taro <- function(t,v=80,d=2400){
to=d/v # time for oneway trip
if((t%/%to)%%2==0) return(v*t%%to)
else return(d - v*t%%to)
}
taro=Vectorize(taro)
t=seq(0,300,0.1)
plot(t,taro(t,v=80),type='l',bty='l',xlab='時間',ylab='Aからの距離',axes=F)
axis(2)
axis(1,labels = F)
jiro <- function(t,.v=70,.d=2400){
.d - taro(t,v=.v,d=.d)
}
jiro=Vectorize(jiro)
lines(t,jiro(t),col=2)
legend('bottom',bty='n',legend=c('太郎','次郎'),col=1:2,lwd=1)
発展問題を考えてみた。
太郎君と次郎君が同時に出発してAとBの間を往復を繰り返します。
ＡからＢへ向かって太郎君が，ＢからＡへ向かって次郎君が進みます。
ＡとＢ地点の間の距離は２４００メートルです。２回目に出会った地点は１回目に出会った地点よりも３２０メートルＡ側にずれた地点でした。
７回目に会う場所はA地点からどれだけ離れた点か答えなさい。
## distance between taro & jiro
dtj <- function(t,vT=80,vJ=70,d=2400){
jiro(t,vJ,d) - taro(t,vT,d)
}
t=seq(0,500,0.25)
plot(t,dtj(t),type='l',axes=F) ; abline(h=0,lty=3)
axis(2) ; axis(1,labels=F)
uniroot(dtj,c(50,100)) # 3rd encounter
taro(80) # its location
uniroot(dtj,c(200,210)) # 7th encounter
taro(208) # its location
taro(240) ; jiro(240) # 8th at point A
round(dtj(16+32*0:19),10)
data.frame(distance=taro(16+32*0:19))
# where is n_th encouter?
nthe <- function(n) taro(16+32*0:14)[ifelse(n%%15,n%%15,15)]
nthe=Vectorize(nthe)
nthe(777)
n=1:100
plot(n,nthe(n),type='l',xlab='n-th encounter',ylab='distance from A')
横軸を出会いが何回めか、縦軸に出会った点のAからの距離としてグラフにしてみた。
Vt:太郎の速度、Vj:次郎の速度
A1:１回目の出会いの点、A2=2回目の出会いの点
Vt/Vj=A1/(2400-A1)=((2400-A1)+(2400-A2))/(A1+A2)
A1=x、A2=x-320から
Vt/Vj=x/(2400-x)=((2400-x)+(2400-(x-320))) / (x+x-320)
これを解くとx=1280なので
Vt/Vj=1280/(2400-1280)=8/7
D=2400,d=320
y=x/(D-x)=((D-x)+(D-(x-d))) / (x+x-d)
x = (d + 2 D) /4
Vt/Vj = (2 D + d)/(2 D - d)
((D-x)+(D-(x-d))) - (x+x-d) where x = (d + 2 D) /4
== d
## 元利均等返済の支払総額 - 元金均等返済の支払総額
# D:借入額 r:月利(年利/12) N:返済月数
Dd <- function(D=10^8,r=0.01/12,N=120) D*N*r*(1+r)^N/((1+r)^N-1) - D*( 1 + r*(N+1)/2)
Dd()
１億円を年利１％で１０年返済で借りたとする。
元利均等返済の支払総額
元金均等返済の支払総額
の差はいくらか？
HKEY_LOCAL_MACHINE\SYSTEM\CurrentControlSet\Services\UsbStor
この中の「Start」の値を「4」にすればUSBメモリが使えなくなり、「3」にすればUSBメモリが使えるようになるという
Windows 10で自動サインインするには、次の手順にしたがって「netplwiz」というコマンドで設定を変更すればよい。
自動サインインは便利な反面、パスワードの入力を省くことにより、第三者に勝手にパソコンを利用されるリスクがあるなどの懸念がある。
しかし、個人利用のみで、自宅でしか使っていないパソコンなら、その種の心配は少ないだろう。
パスワードの入力の煩雑さにイライラしていた人は、ぜひ自動サインインで自宅の自分パソコンの起動を快適にして利用してみてはいかがだろうか。
https://news.livedoor.com/article/detail/17065047/ 左翼は正論で反駁するからダメなんだよね愚民というものの性質が分かってない。だから選挙で敗ける。
クリプトン電球(LDS100V54W)
LED電球(LDA6LHE17BHS)
>>747 スリープ解除時のパスワード入力を省略する
[スタートボタン] をクリックして [設定] をクリックします。
startsetting
[アカウント] をクリックします。
account
[サインインオプション] をクリックします。
「しばらく操作しなかった場合に・・・」から [常にオフ] を選択します。
pm=permutations(1:20,5)
f <- function(x,n) sum(any(1:5==x))==n
s=numeric(5)
for(i in 1:5){
s[i]=sum(apply(pm,1, function(x) f(x,i)))
}
s
rm(list=ls())
options(digits=22)
library(gtools)
pm=permutations(20,5,1:20) # 1-20から5個の順列
f <- function(x,n) sum(1:5==x)==n # 配列xのｎ番目にｎが配置された数を返す
s=numeric(5)
for(i in 1:5){
s[i]=sum(apply(pm,1, function(x) f(x,i))) #i番目がiの数(=正解数)を返す
}
# s 375045 41270 2410 75 1
N=choose(20,5)*factorial(5) # 1860480 20順列5
MASS::fractions(sum((1:5)*s)/N) # 期待値の分数表示
N-sum(s) # 1441679 ０点の場合の数
P0=(N-sum(s))/N
MASS::fractions(P0) # ０点の確率
P=c(P0,s/N) #０点～５点の確率
score=permutations(6,8,0:5,repeats=TRUE) # ８問のすべての点数(0-5)の順列
total_score=apply(score,1,sum) # 総得点の数列
(si=score[total_score>=24,]) # 総得点24点以上の数列
g <- function(x) prod(P[x+1]) # 点数配列→その確率
sum(apply(si,1,g) #その点数(24点以上）になる確率の総和
社労士試験２ <- function(
n20=20, # 選択肢数
n5=5, # 空欄数
n8=8, # 問題数
n24=24 # 合格最低点
){
library(gtools)
library(gmp)
pm=permutations(n20,n5,1:n20)
f <- function(x,n) sum(1:n5==x)==n
s=numeric(n5)
for(i in 1:n5){
s[i]=sum(apply(pm,1, function(x) f(x,i)))
}
N=chooseZ(n20,n5)*factorial(n5)
s0=N-sum(s)
S=c(s0,s)
score=permutations(n5+1,n8,0:n5,repeats=TRUE)
s24=score[apply(score,1,sum)>=n24,]
n=as.bigz(0) # numerator
for(i in 1:nrow(s24)){
n=add.bigz(n,prod.bigz(S[s24[i,]+1]))
}
P=n/(N^n8) # 分数表示
nP=asNumeric(P) # 少数表示
list(P,nP)
}
社労士試験２(20,5,8,24)
社労士試験２(15,5,8,30)
f <- function(Box,Sum){ # Box:箱の数,Sum：入った数字の合計の値
# 重複を許してｎ個からｒ個を選ぶ組み合わせを列挙する
H <- function(n, r, v=1:n) {
if (r == 0)
NULL
else if (r == 1)
matrix(v, n, 1)
else if (n == 1)
matrix(v, 1, r)
else rbind(cbind(v[1], H(n, r - 1, v)), H(n - 1, r, v[-1]))
}
h=H(Box,Sum-Box) # Box個の中から重複を許してSum-Box個を選ぶ
nh=nrow(h) # その組み合わせ数
re=matrix(rep(NA,Box*nh),nrow=nh,ncol=Box) # メモリ確保
a=numeric(Box)
for(i in 1:nh){ # 各々の選び方iに対して
for(j in 1:Box) a[j]=sum(j==h[i,]) # どの箱が何個選択されたかを
re[i,] =a # reのi行に入れる
}
return(re+1) # 1から始まる分を補正
}
箱３個合計９の場合
> f(Box=3,Sum=9)
'%=>%' = function(P,Q) !(P & !Q)
(gr=expand.grid(c(T,F),c(T,F)))
f <- function(P,Q) (P %=>% (Q & !Q)) %=>% !P
mapply(f,gr[,1],gr[,2])
# ロシアのワクチンは旧ソ連の人工衛星にちなみ「スプートニクＶ」と名付けられた。
# ランセットに掲載された論文によると、
# ７６人を対象に第１相および第２相の治験を行ったところ、
# 全員が新型コロナウイルスに対する抗体を獲得したという。
# 米Ｊ＆Ｊ、コロナワクチン治験中断 参加者が原因不明の病気
# 同社は９月、新型コロナワクチンの治験の最終段階に当たる第３相試験に着手したと発表。
# 最大６万人を対象に安全性や有効性を確認するとしていた。
# 治験が再開されて6万例でこの奇病1例だけと仮定して発生割合を1/60000とする。
# ロシアのワクチンではこの奇病の報告はないから発生割合は0/76
# 奇病発生率1/60000と0/76では、どちらが奇病発生が少ないといえるか？
rm(list=ls())
source('tools.R')
# Jeffereys prior
a=b=0.5
par(mfrow=c(2,1))
curve(dbeta(x,a+0,b+76),bty='l')
curve(dbeta(x,a+1,b+59999),col=2,bty='l')
k=1e6
SP=rbeta(k,a+0,b+76)
JJ=rbeta(k,a+1,b+59999)
mean(SP/JJ>1)
mean(SP-JJ>0)
jags4prop(0,1,76,60000,0.5,0.5)
# Uniform prior
a=b=1
par(mfrow=c(2,1))
curve(dbeta(x,a+0,b+76),bty='l')
curve(dbeta(x,a+1,b+59999),col=2,bty='l')
k=1e6
SP=rbeta(k,a+0,b+76)
JJ=rbeta(k,a+1,b+59999)
mean(SP/JJ>1)
mean(SP-JJ>0)
jags4prop(0,1,76,60000,1,1)
jags4prop <- function(r1,r2,n1,n2,alpha=1,beta=1,
ROPEdiff=c(-0.025,0.025),ROPErate=c(0.80,1.25),
NNT=FALSE){
library(rjags)
y=c(rep(1,r1),rep(0,n1-r1),rep(1,r2),rep(0,n2-r2))
s=as.numeric(factor(c(rep('D',n1),rep('U',n2))))
a=alpha ; b=beta # JAGS prior : beta(alpha,beta)
myData=data.frame(y=y,s=s)
Ntotal = length(y)
Nsubj = length(unique(s))
dataList = list(
y = y ,
s = s ,
Ntotal = Ntotal ,
Nsubj = Nsubj
)
# JAGS model
modelString = paste0("
model {
for ( i in 1:Ntotal ) {
y[i] ~ dbern( theta[s[i]] )
}
for ( sIdx in 1:Nsubj ) {
theta[sIdx] ~ dbeta(", a,',' , b," )
}
}
")
writeLines( modelString , con="TEMPmodel.txt" )
jagsModel = jags.model( file="TEMPmodel.txt" , data=dataList, quiet=TRUE)
update(jagsModel)
codaSamples = coda.samples( jagsModel , variable="theta", n.iter=10000 )
mcmcMat=as.matrix(codaSamples)
rate1=mcmcMat[,1]
rate2=mcmcMat[,2]
x11()
par(mfrow=c(2,2))
BEST::plotPost(rate1,col='gray')
if(NNT){
BEST::plotPost(abs(1/(rate1-rate2)), xlab ='NNT(NNH)',col='pink')}
else{
BEST::plotPost(rate1-rate2,compVal=0,ROPE=ROPEdiff,cex=1,col='pink')
}
BEST::plotPost(rate2,col='gray')
BEST::plotPost(rate1/rate2,compVal=1,ROPE=ROPErate,col='skyblue')
invisible(codaSamples)
}
source('tools.R')
# Jeffereys prior
a=b=0.5
par(mfrow=c(2,1))
curve(dbeta(x,a+0,b+76),bty='l')
curve(dbeta(x,a+1,b+59999),col=2,bty='l')
k=1e6
SP=rbeta(k,a+0,b+76)
JJ=rbeta(k,a+1,b+59999)
mean(SP/JJ>1)
mean(SP-JJ>0)
BEST::plotPost(SP/JJ,compVal = 1)
BEST::plotPost(SP-JJ,compVal = 0)
jags4prop(0,1,76,60000,0.5,0.5)
# Uniform prior
a=b=1
par(mfrow=c(2,1))
curve(dbeta(x,a+0,b+76),bty='l')
curve(dbeta(x,a+1,b+59999),col=2,bty='l')
k=1e6
SP=rbeta(k,a+0,b+76)
JJ=rbeta(k,a+1,b+59999)
mean(SP/JJ>1)
mean(SP-JJ>0)
BEST::plotPost(SP/JJ,compVal = 1)
BEST::plotPost(SP-JJ,compVal = 0)
jags4prop(0,1,76,60000,1,1)
安倍・自由移民党のおかげや
日本女性の梅毒患者数はこの5年間で25倍に増加
://biz-journal.jp/2017/03/post_18252.html
>>756 > # 全員が新型コロナウイルスに対する抗体を獲得したという。
ワロタ
options(digits=22)
par(bty='l')
par(mfrow=c(2,1))
f <- function(x) x^x
curve(f(x),-0.1,1)
D(expression(x^x),'x')
f1 <- function(x) x^(x - 1) * x + x^x * log(x)
curve(f1(x),-0.1,1) ; abline(h=0,lty=3)
uniroot(f1,c(0.01,1)) ; 1/exp(1)
f(1/exp(1)) ; exp(-1/exp(1))
>>762 値に０や１があるとカイ二乗検定が使えないから、ベイズ統計で処理することになるね。
sim <- function(n){
a=numeric()
a[1]=0
if(n==1) return(a)
a[2]=sample(0:2,1)
if(n==2) return(a)
for(i in 3:n){
x=sample(0:2,1)
a[i]=x
if(x==0){
i_max=max(which(a[1:(i-1)]==0))
b=a[(i_max+1):(i-1)]
if(all(b!=2)){
b[b==1]=0
a[(i_max+1):(i-1)]=b
}
}
}
return(a)
}
"
時刻t=0に、黒板に数字0が書かれている。
各時刻t=1,2,3,...において、数字0,1,2を下図のように1つずつ横一列に書いていく。
どの数字が書かれるかは同様に確からしい。
（t=0のとき）0
（t=5のときの一例）011212
各時刻tにおいて、数字を1つ書き終えた後、以下の操作を一回行う。
【操作】
この時刻に書かれた数字が0であった場合、そこから最も近い位置の0を探す。
この2つの0で挟まれた数字列の中に1がある場合、それら全てを0に書き換える。
ただしこの数字列の中に2が1つでも含まれる場合は、数字列に対する何らの操作も行わない。
"
rm(list=ls())
f<- function(t){ # 時刻tでの数列aを返す
a=numeric()
a[1]=0 # a[1]=0, t=0での数列
if(t==0) return(a)
for(i in 2:(t+1)){
x=sample(0:2,1) # 追加する数字0,1,2
a[i]=x
if(x==0){ # 0であれば
i_max=max(which(a[1:(i-1)]==0)) # i_max:追加前の最後の0のindex
b=a[(i_max+1):(i-1)] # b:追加前の最後の0からの追加した0を除く数列
if(all(b!=2)){ # bに2が含まれなければ
b[b==1]=0 # bの１を0に置き換えて
a[(i_max+1):(i-1)]=b # aの配列に置換する
}
}
}
return(a)
}
f(10)
sim <- function(n) sum(f(n)==0)
mean(replicate(1e4,sim(10)))
# 書かれた数列から変換後の結果を返す
f<- function(y=c(1,1,0,1,2,0,1)){
t=length(y)
a=numeric(t+1)
a[1]=0 # a[1]=0, t=0での数列
if(t==0) return(a)
for(i in 2:(t+1)){
x=y[i-1]
a[i]=x
if(x==0){ # 0であれば
i_max=max(which(a[1:(i-1)]==0)) # i_max:追加前の最後の0のindex
b=a[(i_max+1):(i-1)] # b:追加前の最後の0からの追加した0を除く数列
if(all(b!=2)){ # bに2が含まれなければ
b[b==1]=0 # bの１を0に置き換えて
a[(i_max+1):(i-1)]=b # aの配列に置換する
}
}
}
return(a)
}
f(c(1,1,0))
f(c(1,1,0,1,2,0,1))
> f(c(1,1,0))
[1] 0 0 0 0
> f(c(1,1,0,1,2,0,1))
[1] 0 0 0 0 1 2 0 1
問題：
シリツ医 ならば (馬鹿 ならば 裏口 である) という命題が真であるときに結論できるのは以下のいずれか？
1 : シリツ医 ならば (裏口 ならば 馬鹿 である)
2 : 馬鹿 ならば (シリツ医 ならば 裏口 である)
3 : 馬鹿 ならば (裏口 ならば シリツ医 である)
4 : 裏口 ならば (シリツ医 ならば 馬鹿 である)
5 : 裏口 ならば (馬鹿 ならば シリツ医 である)
# ならば の定義：(P かつ (Qでない))ではない
'%=>%' = function(P,Q) !(P & !Q)
A = function(S,B,U) S %=>% (B %=>% U)
B1 = function(S,B,U) S %=>% (U %=>% B)
B2 = function(S,B,U) B %=>% (S %=>% U)
B3 = function(S,B,U) B %=>% (U %=>% S)
B4 = function(S,B,U) U %=>% (S %=>% B)
B5 = function(S,B,U) U %=>% (B %=>% S)
C1 = function(S,B,U) A(S,B,U) %=>% B1(S,B,U)
C2 = function(S,B,U) A(S,B,U) %=>% B2(S,B,U)
C3 = function(S,B,U) A(S,B,U) %=>% B3(S,B,U)
C4 = function(S,B,U) A(S,B,U) %=>% B4 (S,B,U)
C5 = function(S,B,U) A(S,B,U) %=>% B5 (S,B,U)
gr=expand.grid(c(T,F),c(T,F),c(T,F))
all(mapply(C1,gr[,1],gr[,2],gr[,3]))
all(mapply(C2,gr[,1],gr[,2],gr[,3]))
all(mapply(C3,gr[,1],gr[,2],gr[,3]))
all(mapply(C4,gr[,1],gr[,2],gr[,3]))
all(mapply(C5,gr[,1],gr[,2],gr[,3]))
D2 = function(S,B,U) B2(S,B,U) %=>% A(S,B,U)
all(mapply(D2,gr[,1],gr[,2],gr[,3]))
"
問題 ： 「シリツ医 ならば (馬鹿 ならば 裏口 である)」という命題と同値な命題はどれか？
1 : シリツ医 ならば (裏口 ならば 馬鹿 である)
2 : 馬鹿 ならば (シリツ医 ならば 裏口 である)
3 : 馬鹿 ならば (裏口 ならば シリツ医 である)
4 : 裏口 ならば (シリツ医 ならば 馬鹿 である)
5 : 裏口 ならば (馬鹿 ならば シリツ医 である)
"
# PならばQ ≡ (P かつ (Qでない))ではない
'%=>%' = function(P,Q) !(P & !Q)
# premise
A = function(S,B,U) S %=>% (B %=>% U)
# choice
B1 = function(S,B,U) S %=>% (U %=>% B)
B2 = function(S,B,U) B %=>% (S %=>% U)
B3 = function(S,B,U) B %=>% (U %=>% S)
B4 = function(S,B,U) U %=>% (S %=>% B)
B5 = function(S,B,U) U %=>% (B %=>% S)
# premise => choice
C1 = function(S,B,U) A(S,B,U) %=>% B1(S,B,U)
C2 = function(S,B,U) A(S,B,U) %=>% B2(S,B,U)
C3 = function(S,B,U) A(S,B,U) %=>% B3(S,B,U)
C4 = function(S,B,U) A(S,B,U) %=>% B4(S,B,U)
C5 = function(S,B,U) A(S,B,U) %=>% B5(S,B,U)
# combination grid of TRUE & FALSE
gr=expand.grid(c(T,F),c(T,F),c(T,F))
# test for premise => choice
all(mapply(C1,gr[,1],gr[,2],gr[,3]))
all(mapply(C2,gr[,1],gr[,2],gr[,3])) # TRUE
all(mapply(C3,gr[,1],gr[,2],gr[,3]))
all(mapply(C4,gr[,1],gr[,2],gr[,3]))
all(mapply(C5,gr[,1],gr[,2],gr[,3]))
# choice -> premise
D1 = function(S,B,U) B1(S,B,U) %=>% A(S,B,U)
D2 = function(S,B,U) B2(S,B,U) %=>% A(S,B,U)
D3 = function(S,B,U) B3(S,B,U) %=>% A(S,B,U)
D4 = function(S,B,U) B4(S,B,U) %=>% A(S,B,U)
D5 = function(S,B,U) B5(S,B,U) %=>% A(S,B,U)
# test for choice -> premise
all(mapply(D1,gr[,1],gr[,2],gr[,3]))
all(mapply(D2,gr[,1],gr[,2],gr[,3])) # TRUE
all(mapply(D3,gr[,1],gr[,2],gr[,3]))
all(mapply(D4,gr[,1],gr[,2],gr[,3]))
all(mapply(D5,gr[,1],gr[,2],gr[,3]))
忘年会は自粛。罹ると面倒くさいし。
14日間隔離、家族や職場、飲みの近くにいる連中も検査して隔離され迷惑もかける。
さらに他人になんか言われそうだしな。
こんな面倒な病気に罹るのはマイナス面しかない
is.wholenumber <- function(x, tol = .Machine$double.eps^0.5) abs(x - round(x)) < tol
# combination grid of TRUE & FALSE
gr=expand.grid(c(T,F),c(T,F),c(T,F))
colnames(gr)=c('S','B','U')
# PならばQ ≡ (P かつ (Qでない))ではない
'%=>%' = function(P,Q) !(P & !Q)
# premise
A = function(S,B,U) S %=>% (B %=>% U)
# choice
B1 = function(S,B,U) S %=>% (U %=>% B)
B2 = function(S,B,U) B %=>% (S %=>% U)
B3 = function(S,B,U) B %=>% (U %=>% S)
B4 = function(S,B,U) U %=>% (S %=>% B)
B5 = function(S,B,U) U %=>% (B %=>% S)
gr
A =mapply(A , gr[,1],gr[,2],gr[,3])
B1=mapply(B1, gr[,1],gr[,2],gr[,3])
B2=mapply(B2, gr[,1],gr[,2],gr[,3])
B3=mapply(B3, gr[,1],gr[,2],gr[,3])
B4=mapply(B4, gr[,1],gr[,2],gr[,3])
B5=mapply(B5, gr[,1],gr[,2],gr[,3])
cbind(gr,A,B1,B2,B3,B4,B5)
オリンピック中止を国民に伝える前に、コロナのせいにするためGOTOキャンペーン推進中というのはうがった見方？？
モウロクジジイ菅ｗ
意味不明なことばかり言ってるお前が国民に理解されるべきだろうがｗ
菅って、陰湿・陰険な老害、説明能力ゼロの無理筋悪代官丸出し
総合的俯瞰的w
いくら頭が悪いにしても無理がありすぎ
この一ヶ月で分かった菅の特徴
・陰湿・陰険
・聞かれたことに答えない不誠実さ、トンチンカン、ピント外れ
・説明能力ゼロだから、答えずに逃げる
・論点ずらし
・同じ言葉の繰り返し
・やったこと自慢の昔話
・インタビューでも用意された原稿丸読み棒読みｗ
・自著で、早速、公文書管理の項目を改竄w
やってることも後付け言い訳もヤバすぎるだろ。ピント外れの陰湿モウロク爺さんを通り越してるぞｗ
米国が移民政策成功してるのって弱者が病気になろうと
気にせずゴミのように放置できるから社会コストが跳ね上がらないから。
日本だとこういうのもみんな無料医療で国保にタカらせ集中治療室まで使わせるからパンクする
>>780 フォルダのプロパティで
共有の設定も必要。
f = function(n,M=100) {
x=c(rep(0,n-1),M)
m=mean(x)
sd=sd(x)*sqrt((n-1)/n)
50+10*(M-m)/sd
}
f=Vectorize(f,vect='n')
f(10:15)
f(10:15,runif(1,1,1000))
裏口容疑者のシリツ医だとこういう計算は無理だろうな。
ある模試でクラスの中でひとりだけ満点、残りは全員０点であったとする。満点の学生の偏差値が80を超えるにはクラスに最低何人いる必要があるか？
"
【たばこ】喫煙率 男女合わせて16.7％(男性27.1％ 女性7.6％) 調査開始以降最低に [ばーど★]
厚生労働省は去年11月、全国の20歳以上の男女およそ5700人を対象に、生活習慣などを調査しました。
16.7*(m+f)=27.1*m + 7.6*f
x=m/f
16.7(x+1)=27.1*x + 7.6
solve 16.7(x+1)=27.1*x + 7.6 for x
x=8/7
"
5700*(8/15)
5700*(7/15)
#
https://www.stat.go.jp/data/jinsui/pdf/201802.pdf Male=sum(c(321,320,359,396,473,482,413,380,380,470,372,301,218,120,43,7,1))*1e4
Fem=sum(c(303,305,346,385,460,471,408,381,391,502,421,373,315,226,118,35,6))*1e4
prop.test(c(5700*8/15,Male),c(5700,(Male+Fem)))
poisson.test(c(5700*8/15,Male),c(5700,(Male+Fem)))
#
https://www.stat.go.jp/data/jinsui/pdf/201802.pdf Male=sum(c(321,320,359,396,473,482,413,380,380,470,372,301,218,120,43,7,1))*1e4
Fem=sum(c(303,305,346,385,460,471,408,381,391,502,421,373,315,226,118,35,6))*1e4
prop.test(c(5700*7/15,Male),c(5700,(Male+Fem)))
poisson.test(c(5700*7/15,Male),c(5700,(Male+Fem)))
p=Male/(Male+Fem)
binom.test(5700*7/15,5700,p)
>>783 "
16.7*(m+f)=27.1*m + 7.6*f
x=m/f
16.7(x+1)=27.1*x + 7.6
solve 16.7(x+1)=27.1*x + 7.6 for x
x=7/8
"
x=(16.7-7.6)/(27.1-16.7)
5700*(7/15)
5700*(8/15)
#
https://www.stat.go.jp/data/jinsui/pdf/201802.pdf Male=sum(c(321,320,359,396,473,482,413,380,380,470,372,301,218,120,43,7,1))*1e4
Fem=sum(c(303,305,346,385,460,471,408,381,391,502,421,373,315,226,118,35,6))*1e4
prop.test(c(5700*7/15,Male),c(5700,(Male+Fem)))
poisson.test(c(5700*7/15,Male),c(5700,(Male+Fem)))
p=Male/(Male+Fem)
binom.test(5700*7/15,5700,p)
rm(lisit=ls())
"
（1）Σ[k=1,n] k! の一の位の数字について、その偶奇を調べよ。
（2）Σ[k=1,n] k! が3の倍数となるためのnの条件を求めよ。
"
library(gmp)
f <- function(n){
re=as.bigz(0)
for(i in 1:n){
re = re + factorialZ(i)
}
asNumeric(re %% 10)
}
y=sapply(1:1000,f)
y[1:100]
y[900:1000]
【たばこ】喫煙率 男女合わせて16.7％(男性27.1％ 女性7.6％) 調査開始以降最低に [ばーど★]
厚生労働省は去年11月、全国の20歳以上の男女およそ5700人を対象に、生活習慣などを調査しました。
http://2chb.net/r/newsplus/1603849457/ 人 口 推 計－ 平 成 30 年 ２ 月 報 －
https://www.stat.go.jp/data/jinsui/pdf/201802.pdf の平成30年２月１日現在 (概算値)から成人の数の概算をだすと
男性：5056万人 女性5446万人になる。
喫煙率調査につかった5700人の男性割合は比較して
日本全体で5056万/(5056万+5446万)の母集団からランダムサンプリングされたと考えてよいか？
library(gtools)
a=combinations(6,2)
f <- function(x){
b=combinations(4,2,(1:6)[-x])
re=NULL
for(i in 1:6){
tmp=c(x,b[i,],(1:6)[-c(x,b[i,])])
re=rbind(re,tmp)
}
re
}
f(a[1,])
res=NULL
for(i in 1:15) res=rbind(res,f(a[i,]))
rownames(res)=NULL
res
v=LETTERS[res]
ans=matrix(v,ncol=ncol(res))
colnames(ans) = c('x','x','y','y','z','z')
print(ans,quote=F)
長方形ABCDの内部の点をPとして
PA=3,PB=4,PC=5のとき長方形の面積の最大値を求めよ。
x<m, y<l
x^2 + (y-l)^2=a^2 (1)
x^2 + y^2 =b^2 (2)
(x-m)^2 + y^2=c^2 (3)
(1)-(2)
l^2 -2yl = a^2-b^2
l=y+sqrt(y^2+a^2-b^2)
(3)-(2)
m^2 -2xm =c^2-b^2
m=x+sqrt(x^2+c^2-b^2)
lm=(y+sqrt(y^2+a^2-b^2))*(x+sqrt(x^2+c^2-b^2))
(2) x=b*cosθ, y=b*sinθ
"
rm(list=ls())
f <- function(a=3,b=4,c=5){
lm <- function(θ) (b*sin(θ)+sqrt((b*sin(θ))^2+a^2-b^2))*(b*cos(θ)+sqrt((b*cos(θ))^2+c^2-b^2))
curve(lm(x),asin(sqrt(b^2-a^2)/b),pi/2)
opt=optimise(lm,c(asin(sqrt(b^2-a^2)/b),pi/2),maximum = TRUE)
θ=opt$maximum
x=b*cos(θ); y=b*sin(θ)
l=y+sqrt(y^2+a^2-b^2)
m=x+sqrt(x^2+c^2-b^2)
data.frame(l=l,m=m,Area=opt$objective)
}
安倍政権が在留ベトナム人を増やした
第2次安倍政権 2012年12月26日～2020年9月16日
在留ベトナム人
2012年 5万2367
↓
2019年 41万1968人
外国人摘発1・1万人超 ベトナム、中国で過半数
https://www.nikkei.com/article/DGXMZO57608760T00C20A4CE0000/ 在留外国人、２９３万人で最多 不法残留は６年連続増―入管庁
https://www.jiji.com/jc/article?k=2020032701013&;g=soc
＞ベトナムは不法残留も３９．８％急増し、１万５５６１人で最多。以下、韓国（１万２５６３人）、中国（１万９０２人）の順となった。
スカ総理って論理的に説明できる能力が皆無なんじゃないのか？
記者 「10年間くらい(消費税)引き上げなくてもいいという、その根拠ついては何だと考えられているのか」
菅 「まさに、アベノミクスを推進をし、経済を成長させる。まさに、経済成長…え…経済を再生させると、させなければ、財政健全化ないという、その政策のである」
https://twitter.com/shin19infinity/status/1304367586738487297
アベちゃん以上にひどいじゃないか。完全に耄碌ジジイ。
安倍のほうがマシだったという時代が来そうだな。
https://twitter.com/5chan_nel (5ch newer account) 本当に経営者ってのはセコいやつばかりだなw
無利息融資とかも、大半が数字いじって申請してんだろコレw
普段は自分達のことを｢経営者｣とかいって偉ぶってるくせにやってることは、労基法ムシシタリ嘘の求人で人を集めたりセクハラパワハラ、そしてコロナ禍での火事場泥棒w
品性下劣なバカにはヤレヤレ
derive (sqrt(a^2-x^2)+sqrt(b^2-x^2))*(x+sqrt(x^2+c^2-b^2))
f(x) = (sqrt(a^2-x^2)+sqrt(b^2-x^2))*(x+sqrt(x^2+c^2-b^2))
f'(x) =(sqrt(a^2 - x^2) + sqrt(b^2 - x^2)) (x/sqrt(-b^2 + c^2 + x^2) + 1) + (-x/sqrt(a^2 - x^2) - x/sqrt(b^2 - x^2)) (sqrt(-b^2 + c^2 + x^2) + x) =0
f'(x)=0
x=a*b/sqrt(a^2+c^2)
長方形ABCDの内部または辺上の点をPとして
PA=3,PB=4,PC=5のとき長方形の面積の最大値と最小値を求めよ。
>>796 一般解が出せたので寝る。
最大値
a=3 b=4 c=5
# l
(a*sqrt(a^2 - b^2 + c^2) + b*c)/sqrt(a^2 + c^2)
# m
(c*sqrt(a^2 - b^2 + c^2) + a*b)/sqrt(a^2 + c^2)
# Area
b*sqrt(a^2 - b^2 + c^2) + a*c
検算
> (a*sqrt(a^2 - b^2 + c^2) + b*c)/sqrt(a^2 + c^2)
[1] 5.612792
> # m
> (c*sqrt(a^2 - b^2 + c^2) + a*b)/sqrt(a^2 + c^2)
[1] 5.696017
> # Area
> b*sqrt(a^2 - b^2 + c^2) + a*c # Area
[1] 31.97056
>448の値と一致
コピペだが激しく同意。
検査希望者が自主的に検査を受けて検査数を増やすやり方では、
いくら検査数が増えても効果が少ないのは、
アメリカや欧州を見てあきらか
おそらく高リスク群なのに検査受けない人が多いんでしょう
中国方式で検査数を増やすのがいちばん確実で効果がある
この地域で〇〇業種で働いてるやつ全員検査うけろ、
とか、この地域の住民全員検査受けろ、
とか、この工場で働いてるやつ全員検査、この学校のやつ全員検査、
みたいに、行政が検査対象を指定して1人も逃さず検査することが重要
正方形ABCDの内部の点をPとしてPA=3,PB=4,PC=5のとき正方形の面積を求めよ。
17 + 4*√(14)
正方形ABCDの内部の点をPとしてPA=１,PB=２,PC=３のとき正方形の面積を求めよ。
5 + 2 * sqrt(2)
正方形ABCDの内部の点をPとしてPA=a,PB=b,PC=cのとき正方形の面積を求めよ。
(1/2)*(a^2 + c^2 + sqrt(-a^4 + 2*a^2*(2*b^2+c^2)-(c^2-2*b^2)^2 ))
√ <- function(x) sqrt(x)
√(3)
俺の知る範囲だけど国内医療機関に補助金で救えと言っているのは自民党医系議員、共産党、れいわ新撰組だな。
俺の知る範囲だけど医療機関を補助金で救えと言っているのは自民党医系議員、共産党、れいわ新撰組だな。
大阪市廃止住民投票の反対割合の99.99%信頼区間。
> binom.confint(692996,692996+675829,conf.level = 0.9999)
method x n mean lower upper
1 agresti-coull 692996 1368825 0.5062707 0.5046081 0.5079332
2 asymptotic 692996 1368825 0.5062707 0.5046081 0.5079333
3 bayes 692996 1368825 0.5062707 0.5046081 0.5079332
4 cloglog 692996 1368825 0.5062707 0.5046069 0.5079320
5 exact 692996 1368825 0.5062707 0.5046077 0.5079336
6 logit 692996 1368825 0.5062707 0.5046081 0.5079332
7 probit 692996 1368825 0.5062707 0.5046081 0.5079332
8 profile 692996 1368825 0.5062707 0.5046081 0.5079332
9 lrt 692996 1368825 0.5062707 0.5046081 0.5079332
10 prop.test 692996 1368825 0.5062707 0.5054328 0.5071086
11 wilson 692996 1368825 0.5062707 0.5046081 0.5079332
>
a=t(combn(5,2))
b=expand.grid(1:10,1:10,1:10)
f <- function(x){
c(a[x[1],],a[x[2],],a[x[3],])
}
y=t(apply(b,1,f))
g <- function(x) !(3 %in% table(x))
i=apply(y,1,g)
sum(i)
z=y[i,]
print(matrix(LETTERS[z],ncol=6),quote=F)
『皆さんには貧しくなる自由があるということだ。何もしたくないなら、何もしなくて大いに結構。その代わりに貧しくなるので、貧しさをエンジョイしたらいい。
ただひとつだけ、その時に頑張って成功した人の足を引っ張るな』。竹中平蔵氏が若者に向けた言葉である。
>>806 A～Eの5人
月曜日、火曜日、水曜日の3日間について、1日2人ずつの宿直を決める。
1回も宿直に当たらない人はいてもよいが、1人で3日すべて宿直に当たるのはナシとするとき、
3日間の宿直の割り振り方は何通りありますか？
A,B,C,D,Eの５人で1日１人の宿直を以下の条件で
日曜日から土曜日まで１週間の日の宿直を割り当てる。
# １週間のうち1回も宿直に当たらない人がいてはいけない
# 誰も2日続けて宿直してはならない
# 前週の土曜日の宿直者を日曜日に宿直させてはならない
# 誰においても7日の宿直日数の上限は２日である
という条件にすると
１週間の宿直割当は何通りあるか？
perm <- function(num, N=5, digit = 7){
r=num%%N
q=num%/%N
while(q > 0 | digit > 1){
r=append(q%%N,r)
q=q%/%N
digit=digit-1
}
return(r+1)
}
pm=NULL
for(i in 0:(5^7-1)){
pm=rbind(pm,perm(i))
}
h <- function(x){
all(1:5 %in% x) & all(diff(x)!=0) & all(table(x)<=2) & x[1]!=1
}
i=apply(pm,1,h)
sum(i)
y=pm[i,]
ans=matrix(LETTERS[y],ncol=7)
colnames(ans)=c('日','月','火','水','木','金','土')
print(head(ans,10),quote=F)
print(tail(ans,10),quote=F)
"更にBは月曜日は都合が悪い、Cは火曜日と木曜日は都合が悪い"
j <- function(x){
all(1:5 %in% x) & all(diff(x)!=0) & all(table(x)<=2) &
x[1]!=1 & x[2]!=2 & x[3]!=3 & x[5]!=3
}
i=apply(pm,1,j)
sum(i)
y=pm[i,]
ans=matrix(LETTERS[y],ncol=7)
colnames(ans)=c('日','月','火','水','木','金','土')
print(head(ans,10),quote=F)
print(tail(ans,10),quote=F)
世界的パンデミック・コロナに自助を要求し、公助が後手後手の菅自民では、今年の年末年始は、リストラ・雇止めで、職を失い、家を失い、蓄えも底をつき、餓死・凍死する人が出る可能性がある。
"
ある病院に内科医A,B,C、外科医D,Eがいて１週間(日～土）の当直と呼び出し待機の割り当てをする。
以下の条件を満たす割り当ては何通りあるか？
(1) 1回も当直に当たらない人がいてはいけない
(2) 誰も続けて当直してはならない(但し、前週の土曜日の当直は考慮しない）
(3) 待機は何日連続してもよい
(4) 内科医が当直のときは待機は外科医、外科医が当直の時は内科医が待機する。
"
ある病院に内科医A,B,C、外科医D,Eがいて１週間(日～土）の当直と呼び出し待機の割り当てをする。
以下の条件を満たす割り当ては何通りあるか？
(1) 1回も当直に当たらない人がいてはいけない
(2) 誰も続けて勤務（当直または待機）してはならない(但し、前週の土曜日の勤務は考慮しない）
(3) 誰においても１週間の当直総数の上限は２日である
(4) 内科医が当直のときは待機は外科医、外科医が当直の時は内科医が待機する。
女性が少ない、若手が少ない、会員に偏りがあるとかよく言う。
自分の選んだ閣僚達こそまさにそうじゃないか。スガは支離滅裂。
ある病院に内科医A,B,C、外科医D,Eがいて１週間(日～土）の当直と呼び出し待機の割り当てをする。
以下の条件を満たす割り当ては何通りあるか？
(1) 1回も当直に当たらない人がいてはいけない
(2) 誰も続けて勤務（当直または待機）してはならない(但し、前週の土曜日の勤務は考慮しない）
(3) 誰においても１週間の当直総数の上限は２日である
(4) 内科医が当直のときは待機は外科医、外科医が当直の時は内科医が待機する。
例
日 月 火 水 木 金 土
当直 A B A C D E D
待機 D E D E A B C
ある病院に内科医A,B,C、外科医D,Eがいて１週間(日～土）の当直と呼び出し待機の割り当てをする。
以下の条件を満たす割り当ては何通りあるか？
(1) 1回も当直に当たらない人がいてはいけない(待機はしなくてもいい)
(2) 誰も続けて勤務（当直または待機）してはならない(但し、前週の土曜日の勤務は考慮しない）
(3) 誰においても１週間の当直総数の上限は２日である（待機の上限はなし）
(4) 内科医が当直のときは待機は外科医、外科医が当直の時は内科医が待機する。
例１
日 月 火 水 木 金 土
当直 A B A B C D E
待機 E D E D E A B
例２
日 月 火 水 木 金 土
当直 A B A C D E D
待機 D E D E A B C
"
ある病院に内科医A,B,C、外科医D,Eがいて１週間(日～土）の当直と呼び出し待機の割り当てをする。
以下の条件を満たす割り当ては何通りあるか？
(1) 1回も当直に当たらない人がいてはいけない(待機はしなくてもいい)
(2) 誰も続けて勤務（当直または待機）してはならない(但し、前週の土曜日の勤務は考慮しない）
(3) 誰においても１週間の当直総数の上限は２日である（待機の上限はなし）
(4) 内科医が当直のときは待機は外科医、外科医が当直の時は内科医が待機する。
"
rm(list=ls())
library(gtools)
pm=permutations(5,7,rep=T)
f <- function(x){ # (1) & 連続当直不可 & (3)
all(1:5 %in% x) & all(diff(x)!=0) & all(table(x)<=2)
}
i=apply(pm,1,f)
sum(i)
y=pm[i,]
ans=matrix(LETTERS[y],ncol=7)
colnames(ans)=c('日','月','火','水','木','金','土')
print(ans[1000,],quote=F) ; (x=y[1000,])
f1 <- function(x){
all(diff(x)!=0) # 連続待機不可
}
y1=pm[apply(pm,1,f1),]
g <- function(x){ # x:当直候補配列
idx=NULL
for(i in 1:nrow(y1)){ # y1=待機候補配列
if(all(x %in% 1:3 == !(y1[i,] %in% 1:3))){ #4
idx=append(idx,i)
}
}
re=NULL
for(i in idx){
cow=FALSE # 連続勤務continual work?
for(j in 1:5){
a=which(j==x) # 当直曜日
b=which(j==y1[i,])# 待機曜日
if(any(diff(sort(c(a,b)))<=1)){ # 連続勤務ならbreak
cow=TRUE
break
}
}
if(!cow) re=append(re,i) # 連続勤務でなければ採用
}
re
}
apply(y[1:15,],1,g)
rei=rbind(LETTERS[x<-y[1,]],LETTERS[y1[g(x)[1],]])
colnames(rei)=c('日','月','火','水','木','金','土') ; rownames(rei)=c('当直','待機')
print(rei,quote=F)
rei=rbind(LETTERS[y[6600,]],LETTERS[y1[g(y[6600,])[16],]])
colnames(rei)=c('日','月','火','水','木','金','土') ; rownames(rei)=c('当直','待機')
print(rei,quote=F)
z=apply(y,1,g)
length(unlist(z)) # 12192通り
nrow(y) ; length(z)
rbind(LETTERS[y[1,]],LETTERS[y1[g(y[1,])[1],]])
print(rbind(LETTERS[y[6600,]],LETTERS[y1[g(y[6600,])[16],]]),quote=F)
library(gtools)
pm=gtools::permutations(6,5,rep=TRUE)
idx=apply(pm,1,function(x) sum(x * 6^(4:0))%%6==0)
sum(idx)
pm[idx,][1000,]
1から6までの数字を使って5ケタの数字を作る。
同じ数字を何回使ってもいいとすると、
(1) 6の倍数は何通りあるか述べよ。
(2) その6の倍数を小さい順に並べたときに1000番目にくる数字を述べよ。
library(gtools)
pm=gtools::permutations(6,5,rep=TRUE)
f <- function(x) sum(x * 10^(4:0))%%6==0
idx=apply(pm,1,f)
sum(idx)
pm[idx,][1000,]
library(gtools)
pm=gtools::permutations(6,5,rep=TRUE)
f <- function(x) sum(x * 10^(4:0))%%6==0
y=pm[apply(pm,1,f),]
head(y,10) ; tail(y,10)
cat(paste(y[1000,],collapse=''))
for(i in 1:length(index)){
cat(i,': ')
cat(paste(y[i,],collapse=''),'\n')
}
"
1から6までの数字を使って5ケタの数字を作ります。
同じ数字を何回使ってもいいとすると、6の倍数は1296通りある。
小さい順に並べたときに1000番目にくる数字を述べよ。
"
library(gtools)
pm=gtools::permutations(6,5,rep=TRUE)
f <- function(x) sum(x * 10^(4:0))%%6==0
y=pm[apply(pm,1,f),]
head(y,10) ; tail(y,10)
cat(paste(y[1000,],collapse=''))
for(i in 1:length(index)){
cat(i,': ')
cat(paste(y[i,],collapse=''),'\n')
}
f1 <- function(x) sum(x * 10^(4:0))%%6
mod6=apply(pm,1,f1)
pm1=cbind(pm,mod6)
head(pm1,30)
matrix(mod6,ncol=6,b=T)
ある病院に内科医A,B,C、外科医D,Eがいて１週間(日～土）の当直と呼び出し待機の割り当てをする。
以下の条件を満たす割り当ては何通りあるか？
(1) 1回も当直に当たらない人がいてはいけない(待機はしなくてもいい)
(2) 誰も続けて勤務（当直または待機）してはならない(但し、前週の土曜日の勤務は考慮しない）
(3) 誰においても１週間の当直総数および待機総数の上限は２日である
(4) 内科医が当直のときは待機は外科医、外科医が当直の時は内科医が待機する。
(5) 当直は２日以上間隔を空ける
例
> print(rei,quote=F)
日 月 火 水 木 金 土
当直 A B D A C E D
待機 D E C E D A B
> print(rei,quote=F)
日 月 火 水 木 金 土
当直 B D E C B A E
待機 E A B D E D B
ある病院に内科医A,B,C、外科医D,Eがいて１週間(日～土）の当直と呼び出し待機の割り当てをする。
以下の条件を満たす割り当ては何通りあるか？
(1) 誰も少なくとも1回は当直および待機に割り当てられる
(2) 誰も続けて勤務（当直または待機）してはならない(前週の土曜日の勤務も考慮する）
(3) 誰においても１週間の当直総数および待機総数の上限は２日である
(4) 内科医が当直のときは待機は外科医、外科医が当直の時は内科医が待機する。
(5) 当直は２日以上間隔を空ける（前週の勤務も考慮する）
>>826 固定だと不均衡も固定だから良くないな。
ある病院に内科医A,B,C、外科医D,Eがいて１週間(日～土）の当直と呼び出し待機の割り当てをする。
以下の条件を満たすように割りあてる。
(1) 誰も少なくとも1回は日～土の間で当直および待機に割り当てられる
(2) 誰も続けて勤務（当直または待機）してはならない。
(3) 誰においても１週間の当直総数および待機総数の上限はどちらも２日である
(4) 内科医が当直のときは待機は外科医、外科医が当直の時は内科医が待機する。
(5) 当直は２日以上の間隔を空ける
今週の勤務割当は次の通りとする。
日 月 火 水 木 金 土
当直 A B D E C B D
待機 D E C B D E A
週を跨いで(1)～(5)の条件を満たす来週の割りあて方は何通りあるか？
割り当ては132通り
例
> print(rei,quote=F)
日 月 火 水 木 金 土
当直 E B A C B D E
待機 C D E D E A B
> print(rei,quote=F)
日 月 火 水 木 金 土
当直 C B E D A B E
待機 E D A B E D C
"
1から6までの数字を使って5ケタの数字を作ります。
同じ数字を何回使ってもいいとすると、6の倍数は1296通りある。
小さい順に並べたときに1000番目にくる数字を述べよ。
"
rm(list=ls())
source('toolmini.R')
library(gtools)
pm=gtools::permutations(6,5,rep=TRUE)
f <- function(x) sum(x * 10^(4:0))%%6==0
y=pm[apply(pm,1,f),]
head(y,10) ; tail(y,10)
cat(paste(y[777,],collapse=''))
# 小さい順に並べたときにn番目にくる数字
order2num <- function(n){
# cat(paste(y[n,],collapse=''),'\n')
a=10*as.numeric(paste(dec2nw(n,6),collapse=''))+11100
a+(1:6)[(a+1:6)%%6==0]
}
n=1:(6^4-1)
plot(n,sapply(n,order2num))
order2num(333)
order2num(777)
ある病院に内科医A,B,C、外科医D,Eがいて１週間(日～土）の当直と呼び出し待機の割り当てをする。
以下の条件を満たすように割りあてる。
(1) 誰も少なくとも1回は日～土の間で当直および待機に割り当てられる
(2) 誰も続けて勤務（当直または待機）してはならない。
(3) 誰においても１週間の当直総数および待機総数の上限はどちらも２日である
(4) 内科医が当直のときは待機は外科医、外科医が当直の時は内科医が待機する。
(5) 当直は２日以上の間隔を空ける
今週の勤務割当は次の通りとする。
日 月 火 水 木 金 土
当直 A B D E C B D
待機 D E C B D E A
週を跨いで(1)～(5)の条件を満たす来週の割りあて方は何通りあるか？
library(gtools)
pm=permutations(5,7,rep=T)
# 当直可能配列
f <- function(x){ # (1) & 連続当直不可 & (3) & (5)（週跨ぎ）
int=NULL
for(i in 1:5){
a=which(i==x) # a : i の当直日
int[i]=ifelse(length(a)==1,TRUE,diff(a)>2) # 当直間隔が２を越えるか？
}
all(1:5 %in% x) & all(diff(x)!=0) & all(table(x)<=2) & all(int) &
all(x[1]!=c(1,2,4)) & # 日曜日A,B,D当直不可
x[2]!=4 # 月曜日D当直不可
}
i=apply(pm,1,f)
sum(i)
y=pm[i,] # 当直可能配列
# 待機可能配列
f1 <- function(x){
all(1:5 %in% x) & all(diff(x)!=0) & all(table(x)<=2) & # 最低1回 & 連続待機不可 & 待機日総数<=2
all(x[1]!=c(1,4)) # 日曜日A,D待機不可
}
y1=pm[apply(pm,1,f1),]
g <- function(x){ # x:当直候補配列
idx=NULL
for(i in 1:nrow(y1)){ # y1=待機候補配列
if(all(x %in% 1:3 == !(y1[i,] %in% 1:3))){ #4 当直医属性!=待機医属性
idx=append(idx,i)
}
}
re=NULL # 条件を満たす待機配列のy1での行index
for(i in idx){
cow=FALSE # 連続勤務continual work?
for(j in 1:5){
a=which(j==x) # 当直曜日
b=which(j==y1[i,])# 待機曜日
if(any(diff(sort(c(a,b)))<=1)){ # 連続勤務ならbreak
cow=TRUE
break
}
}
if(!cow) re=append(re,i) # 連続勤務でなければ採用
}
re
}
gg <- function(x,print=TRUE){
re=g(x)
if(!is.null(re)){
n=length(re)
ans=vector(mode='list',length=n)
for(i in 1:n){
rei=rbind(LETTERS[x],LETTERS[y1[re[i],]])
colnames(rei)=c('日','月','火','水','木','金','土')
rownames(rei)=c('当直','待機')
ans[[i]]=rei
if(print){print(rei,quote=F)
cat('\n')}
}
invisible(ans)
}
}
zz=apply(y,1,gg)
nzz=length(zz)
zzz=NULL
for(i in 1:nzz){
if(!is.null(zz[[i]])) zzz=c(zzz,zz[[i]])
}
print(head(zzz),quote=F)
print(zzz,quote=F)
> print(head(zzz),quote=F)
[[1]]
日 月 火 水 木 金 土
当直 C A E B A D E
待機 E D C D E B A
[[2]]
日 月 火 水 木 金 土
当直 C A E B C D E
待機 E D C D E A B
[[3]]
日 月 火 水 木 金 土
当直 C A E B C D E
待機 E D C D E B A
[[4]]
日 月 火 水 木 金 土
当直 C A E C B D E
待機 E D B D E A C
[[5]]
日 月 火 水 木 金 土
当直 C A E C B D E
待機 E D B D E C A
[[6]]
日 月 火 水 木 金 土
当直 C A E D A B E
待機 E D B C E D A
[[101]]
日 月 火 水 木 金 土
当直 E C B D C A E
待機 B D E A E D C
[[102]]
日 月 火 水 木 金 土
当直 E C B D E A B
待機 B D E A C D E
[[103]]
日 月 火 水 木 金 土
当直 E C B D E A C
待機 B D E A C D E
[[104]]
日 月 火 水 木 金 土
当直 E C B D E B A
待機 B D E A C D E
[[105]]
日 月 火 水 木 金 土
当直 E C B D E B A
待機 B D E C A D E
[[106]]
日 月 火 水 木 金 土
当直 E C B D E C A
待機 B D E C A D E
>>829 これは間違い、106通りだと思う。
バグがなければだけど
>>831 更に
(6) ２週続けて週２回の当直はしてはならない。
を付け加えてみよう。
ある病院に内科医A,B,C、外科医D,Eがいて１週間(日～土）の当直と呼び出し待機の割り当てをする。
以下の条件を満たすように割りあてる。
(1) 誰も少なくとも1回は日～土の間で当直および待機に割り当てられる
(2) 誰も続けて勤務（当直または待機）してはならない。
(3) 誰においても１週間の当直総数および待機総数の上限はどちらも２日である
(4) 内科医が当直のときは待機は外科医、外科医が当直の時は内科医が待機する。
(5) 当直は２日以上の間隔を空ける
(6) ２週続けて週２回の当直はしてはならない。
今週の勤務割当は次の通りとする。
日 月 火 水 木 金 土
当直 A B D E C B D
待機 D E C B D E A
週を跨いで(1)～(6)の条件を満たす来週の割りあて方は何通りあるか？
library(gtools)
pm=permutations(5,7,rep=T)
# 当直可能配列
f <- function(x){ # (1) & 連続当直不可 & (3) & (5)（週跨ぎ）
int=NULL
for(i in 1:5){
a=which(i==x) # a : i の当直日
int[i]=ifelse(length(a)==1,TRUE,diff(a)>2) # 当直間隔が２を越えるか？
}
all(1:5 %in% x) & all(diff(x)!=0) & all(table(x)<=2) & all(int) &
all(x[1]!=c(1,2,4)) & # 日曜日A,B,D当直不可
x[2]!=4 &# 月曜日D当直不可
sum(x==2)<2 & sum(x==4) # B,D の当直は2回未満
}
i=apply(pm,1,f)
sum(i)
y=pm[i,] # 当直可能配列
lwa=rbind(c(1,2,4,5,3,2,4),c(4,5,3,2,4,5,1)) # last week allocation
rei=rbind(LETTERS[c(1,2,4,5,3,2,4)],LETTERS[c(4,5,3,2,4,5,1)])
colnames(rei)=c('日','月','火','水','木','金','土')
rownames(rei)=c('当直','待機')
print(rei,quote=F)
米国が移民政策成功してるのって弱者が病気になろうと
気にせずゴミのように放置できるから社会コストが跳ね上がらないからだろう。
日本は多民族共生できるほど民度が高くないんだよなぁ。
日本だと気の毒だからと国保にタカらせ集中治療室まで使わせるからパンクする
旅行にいく余裕もない人の税金を横取りして旅にでる強盗キャンペーン。
それでコロナが広がるならまさに死神政策。
緊急提言ではさらに、これらの対策を取った上でも、感染状況ごとに分類した四つのステージのうち、感染者が急増している「ステージ3」相当以上と判断された場合には
「社会経済活動に一定の制約を求めるような強い対策を行う必要があることから、国民が一丸となって対策を進めていく必要がある」とした。
https://mainichi.jp/articles/20201109/k00/00m/040/249000c >国民が一丸となって
一丸となったらクラスターが発生ｗ
Keltonの新著を読み始めた。
The Deficit Myth: Modern Monetary Theory and the Birth of the People's Economy (English Edition) Kindle版
この記述は意外だったな。
But even
Senator Bernie Sanders has echoed Reagan, saying, “I am concerned
about the debt. It’s not something we should be leaving to our kids and
our grandchildren.”
The fifth myth is that deficits make the United States dependent on
foreigners. This myth would have us believe that countries like China and
Japan have enormous leverage over us because they hold large
quantities of US debt.
米国債を売ろうという誘惑に言及した総理は不審死したよあなぁ。
zを-1でない複素数として
ω= （z+2i) / (z+1) とおく。
|z|=1のとき、偏角が3π/4となるωを求めよ。
options(digits=5)
f <- function(x){
z=cos(x)+1i*sin(x)
omega=(z+2i)/(z+1)
Arg(omega)
}
curve(f,0,2*pi) ; abline(h=3/4*pi,lty=3)
low=optimise(f,c(4,5),maximum = T)$maximum
(x=uniroot(function(x)f(x)-3/4*pi,c(low,5))$root)
(z=cos(x)+1i*sin(x))
(omega=(z+2i)/(z+1))
z=a+bi
ω=(z+2i)/(z+1)
=(a+bi+2i)/(a+bi+1)
分母子にa+1-biをかけると
分子=(a+bi+2i)(a+1-ib)
分母=(a+1)^2+b^2
ωの偏角が3/4πということは
ωの虚部/ωの実部=tan(3/4π)=-1
分母は実数なので約分されて
分子の虚部/分子の実部=-1
これを変形して
分子の虚部＋分子の実部=0
複素数α+iβをα+βに変形するにはi=1と置換すればいいので
分子の式(a+bi+2i)(a+1-ib)でi=1と置換して
(a+b+2)(a+1-b)=0
∴ a+b+2=0 またはa+1-b=0
|z|=1ゆえa^2+b^2=1
a+b+2=0 かつ a^2+b^2=1に実数解なし
a+1-b=0 かつ a^2+b^2=1 を解くと(a,b)=(-1,0),(0,1)
z≠-1なのでa=0,b=1が残る
z=a+bi (a,bは実数)
ω=(z+2i)/(z+1)
分母子に(a-bi+1)をかけると
分子=(z+2i)(a-bi+1)=(a+bi+2i)(a-bi+1)= (a^2+a+b^2+2b) +i(2a+b+2)
分母=(z+1)(a-bi+1)=(a+bi+1)(a-bi+1)=(a+1)^2+b^2 (実数)
ωの虚部/ωの実部=分子の虚部/分子の実部=tan(4π/3)=-1
これを変形すれば、
分子の実部+分子の虚部=0
複素数α+iβをα+βに変形するにはこの形でi=1と置換すればいいので
分子のiを1に置換して
a^2+a+b^2+2b +(2a+b+2) = a^2+b^2+3a+3b+2=0
|z|=1ゆえa^2+b^2=1なので
連立方程式
a^2+b^2+3a+3b+2=0
a^2+b^2=1
を解くと
a=-1,b=0
または
a=0,b=-1
z≠-1ゆえa=-1,b=0は不適。
候補はa=0,b=-1
z=a+bi=-i
このとき
ω=(z+2i)/(z+1)=i/(1-i) = -0.5+0.5i
偏角=atan(0.5/(-0.5))=(3/4)π
△ABC (∠A＝50°, ∠B＝70°) をAを原点、Bをx軸上に配置する。
△ABCの内部の点をPとしてPA=2 PB=3, PC=4 のとき、
(1)B,C,Pの座標を求めよ。
(2)△PAB,△PBC,△PCAの面積を求めよ
> re$B
[1] 4.9368+0i
> re$C
[1] 3.4432+4.1035i
> re$P
[1] 1.9619+0.3879i
> with(re,ABC2S(P,A,B)) #△PAB
[1] 0.95738
> with(re,ABC2S(P,B,C)) #△PBC
[1] 5.8139
> with(re,ABC2S(P,C,A)) #△PCA
[1] 3.3576
> re$B
[1] 4.9368+0i
> re$C
[1] 3.4432+4.1035i
> re$P
[1] 1.9619+0.3879i
> with(re,ABC2S(P,A,B)) #△PAB
[1] 0.95738
> with(re,ABC2S(P,B,C)) #△PBC
[1] 5.8139
> with(re,ABC2S(P,C,A)) #△PCA
[1] 3.3576
> re$S # △ABC
[1] 10.129
[1] 4.652337六角形AB,CD,EFの辺の長さをn,BC,DE,FAの長さをm、
∠A=degA° ∠C=degC° ∠E=degE°、とする。
m=1,n=2, degA=60,degC=90,degE=120のとき
この六角形の面積を求めなさい。
作図するプログラムを書くのが面白かっただけ。
> Hexagon(1,2,60,90,120)
[1] 4.652337
よくも悪くも、中国共産党の対日外交には虚々実々の駆け引きというか、ある程度の枠がはまっているのに対して、かりに将来、中国の民主化が進んで「反日デモ」的な大衆感情に熱狂的に支持されて議会の多数派を占めるような政権が誕生した場合、日本に対する姿勢が今までと比較にならないくらい強硬になるのではないかという不安は、多くの日本人が感じたことがあるのではないか
中国化する日本 より
>>851 > re=DV2A(50,70,2,3,4)
> attach(re)
> A=0i
> B
[1] 4.936762+0i
> C
[1] 3.443221+4.103471i
> P
[1] 1.961936+0.387857i
> ABC2S(P,A,B) #△PAB
[1] 0.9573792
> ABC2S(P,B,C) #△PBC
[1] 5.813914
> ABC2S(P,C,A) #△PCA
[1] 3.357635
> S # △ABC
[1] 10.12893
> D=intsect(A,P,B,C) ; pt(D,'D')
> seg(P,D,col=2,lty=3)
> E=intsect(A,C,P,B) ; pt(E,'E')
> seg(P,E,col=2,lty=3)
> F=intsect(A,B,C,P) ; pt(F,'F')
> seg(P,F,col=2,lty=3)
> D
[1] 4.605388+0.910444i
> E
[1] 0.4868298+0.5801812i
> F
[1] 1.807311+0i
> detach(re)
こういう毛針に騙されたんだなぁ
# 小数点付きの数numをN進法で表示する(62進法まで対応 0-9,a-z,A-Z)
rm(list=ls())
num=1/3;N=3;kmin=5
decN <- function(num, N, kmin = 5){ # kmin：最小小数点後桁
int=floor(num)
r=int%%N
q=int%/%N
while(q > 0){
r=append(q%%N,r)
q=q%/%N
} # rに整数のN進法表示数列を格納
k=max(nchar(num)-nchar(floor(num))-1,kmin) # 同長もしくはkminの長さの小数表示
a=numeric(k)
x=round(num-floor(num),k) # e.g. 7.28-floor(7.28)!=0.280に対応
for(i in 1:k){
y=round(x*N,k) # e.g. 0.728*5-3.64 !=0 に対応
a[i]=floor(y)
x=y-a[i] # r . a[1] a[2] a[3] ... a[k]
}
b=list(integer=r,decimal=a,num=sum(c(int,a)*(1/N)^(0:k)))
fig=c(0:9,letters,LETTERS)[1:N]
if(N<=62){ # Nが62以下は数値として表示
cat(paste(fig[b$integer+1],sep='',collapse=''),
'.',paste(fig[b$decimal+1],sep='',collapse=''),sep='')
cat('\n')
}
else{ # Nが63以上は整数部分と小数部分を数列で表示
print(b[1:2])
}
invisible(b) # b$num:検証用
}
del=sapply(1:16, function(x) decN(0.1,x,16))
decN(pi,16)
decN(0.1,13,10)
# １３進法 0 1 2 3 4 5 6 7 8 9 A J Q
options(digits=22)
decK <- function(PI=pi,K=10){
x=decN(PI,13,kmin=K)
K <- function(x){
if(x==0) return('0')
else{
c(as.character(1:9),'A','J','Q')[x]
}
}
K=Vectorize(K)
re=paste(c(K(x$integer),'.',K(x$decimal)),collapse = '')
print(re,quote=F)
invisible(re)
}
decK(pi)
decK(exp(1))
decK(sqrt(2))
１４進法 で使う数字を小さい方から0 1 2 3 4 5 6 7 8 9 A J Q Kとするときπ、ネイピア数、√２を１４進法で小数１０桁まで表示せよ。
62進法 で使う数字を小さい方から0 1 2 3 4 5 6 7 8 9 a b c ... x y z A B C ... X Y Z
とするときπ、ネイピア数、√２を１４進法で小数１０桁まで表示せよ。
> decN(pi,62)
3.8MhuCIRym8egOl
> decN(exp(1),62)
2.Ix4FDGbb8J4wtH
> decN(sqrt(2),62)
1.pGeGLWSyyECdM
0と1の2個の数を使いマイナス二進法で1から10を数えよ （マイクロソフトの入社試験）
答と解説は
ダウンロード＆関連動画＞＞
@YouTube 20まで計算させてみた
ans
1 1
2 110
3 111
4 100
5 101
6 11010
7 11011
8 11000
9 11001
10 11110
11 11111
12 11100
13 11101
14 10010
15 10011
16 10000
17 10001
18 10110
19 10111
20 10100
それを面倒にした問題
(1) 2021をマイナス二進法で表示せよ。
(2) 3, 33, 333, 3333を各々マイナス三進法で表示せよ。
MS <- function( # Minus N-ary System
num,
N=-2,
d=16,
print=TRUE
){
base=N^((d-1):0)
pm=expand.grid(replicate(d,0:(-N-1),simplify = FALSE))
colnames(pm)=1:d
f <- function(x) sum(x*base) == num
re=pm[apply(pm,1,f),]
i=1
flg <- re[1]==0
while(flg){
i=i+1
flg <- re[i]==0
}
ans=paste(as.character(re[i:d]),collapse='')
if(print) print(ans,quote=F)
invisible(ans)
}
data.frame(ans=sapply(1:20,function(n)MS(n,p=F)))
MS(2021,-2)
MS(3,-3,d=3)
MS(33,-3,d=5)
MS(333,-3,d=7)
MS(3333,-3,d=9)
3を0,1,2の3つの数字をつかったマイナス三進法で表すと3 = 1*(-3)^2 + 2*(-3) + 0*(-3)^0なので 120と表せる。
1から10までをマイナス三進法で表示すると
1 1
2 2
3 120
4 121
5 122
6 110
7 111
8 112
9 100
10 101
問題 ： 円周率をマイナス三進法で小数１０桁まで表示せよ。
MS <- function( # Minus N-ary System
num,
N=-2,
d=16,
print=TRUE
){
base=N^((d-1):0)
pm=expand.grid(replicate(d,0:(-N-1),simplify = FALSE))
colnames(pm)=1:d
f <- function(x) sum(x*base) == num
re=pm[apply(pm,1,f),]
i=1
flg <- re[1]==0
while(flg){
i=i+1
flg <- re[i]==0
}
ans=paste(as.character(re[i:d]),collapse='')
if(print) print(ans,quote=F)
invisible(ans)
}
piN <- function(N=-2){ # pi for minus N-ary system
Pi=unlist(strsplit(as.character(pi),'.',fixed=T))
seisu=MS(as.numeric(Pi[1]),N,d=3,print=F) # 3(mod10) = 120(mod-3)
pm=expand.grid(replicate(10,0:(abs(N)-1),simplify = F))
base=(1/N)^(1:10)
f <- function(x) (pi-floor(pi)- sum(x*base))^2
dif=apply(pm,1,f)
shosu=paste(as.character(pm[which.min(dif),]),collapse='')
print(paste0(seisu,'.',shosu),quote=F)
}
> piN(-2)
[1] 111.0110010001
> piN(-3)
[1] 120.0220210200
> piN(-5)
[1] 3.0434333021
# e+0*e^0+1*e^(-1)+0*e^(-2)+1*e^(-3)
# [1] 3.135948
n=10
e=exp(1)
1*e^1+0*e^0 < pi
pi < 1*e^1 + 1*e^1
a=numeric()
b=numeric()
b[1]=e+0*e^0+e^(-1)
a[1]=as.numeric(b[1]<pi)
for(i in 1:n){
a[i+1]=as.numeric((b[i]+e^(-i-1))<pi)
b[i+1]=b[i]+a[i+1]*e^(-i-1)
}
paste(as.character(a),collpse="")
武漢からの飛行機は乗客降ろさず機内で検査。
海外からの入国は全て隔離検査。
電車バスはマスク無しは乗車拒否かつ検温を改札で実施。
店はマスク無しは入店拒否。
マスクはコンビニで無料配布かつスマホで一人一人の枚数管理するアプリを政府が開発。
学校は閉鎖しオンライン授業に切り替え。
ざっと台湾の対策はこんなもの。
# (x-r*cos(θ))^2 + (y-r*sin(θ))^2=r^2
# y = r*sin(θ) + sqrt(r^2*(sin(θ))^2 + 2*r*x -x^2)
area <- function(r,θ){
integrate(function(x) r*sin(θ) + sqrt(r^2*(sin(θ))^2 + 2*r*x -x^2),0,1)$value
}
# (x-r*cos(θ))^2 + (y-r*sin(θ))^2=r^2
# y = r*sin(θ) + sqrt(r^2*(sin(θ))^2 + 2*r*x -x^2)
area <- function(r,θ){
f = function(x) r*sin(θ) + sqrt(r^2*(sin(θ))^2 + 2*r*x -x^2)
O=c(0,0)
P=c(r*cos(θ),r*sin(θ))
Q=c(1,f(1))
integrate(f,0,1)$value
}
rm(list=ls())
source('toolmini.R')
plot(NULL,xlim=c(0,1.5),ylim=c(0,1.5),asp=F,ann=F,axes=F)
abline(h=0,v=0,col=8)
r=1.015
ci <- function(x,R=r) sqrt(R^2-x^2)
cir(0,0,r,lty=4)
x=seq(ci(1),r,0.01)
lines(x,ci(x),type='h',col=4)
Q=ci(1)+1i
seg(Q,ci(1)+0i)
seg(Q,Q+1) ; seg(Q+1,Q+1-1i) ; seg(Q-1i,Q-1i+1)
seg(0i,Q,col=8)
pt(0.05+0.05i,'θ'); pt(Q/2,'r',cex=1.5)
会食が原因になっていることが多いと言っておいて、Gotoイートで会食を促進するという謎の政策を進める政府。
デフレ下に増税するという世襲低学歴の暗愚が最長政権の土人の国になったなぁ。
一方、文明国では
武漢からの飛行機は乗客降ろさず機内で検査。
海外からの入国は全て隔離検査。
電車バスはマスク無しは乗車拒否かつ検温を改札で実施。
店はマスク無しは入店拒否。
マスクはコンビニで無料配布かつスマホで一人一人の枚数管理するアプリを政府が開発。
学校は閉鎖しオンライン授業に切り替え。
source('toolmini.R')
plot(NULL,xlim=c(0,2),ylim=c(-1,1),asp=1,ann=F,axes=T)
O=0i;A=1+0i;B=1i;C=1+1i
pt(O,'O'); pt(A,'A') ; pt(B,'B') ; pt(C,'C')
seg(O,A);seg(0,B);seg(C,A);seg(C,B) ; seg(O,C,lty=3)
r=1.070437
th=-0.3647908 ; pt(0.15-0.025i,'θ') # Pの偏角
P=r*cos(th)+r*1i*sin(th) ; pt(P,'P(rcosθ,rsinθ)') ; seg(O,P,col=8)
Cir(P,r,col=8)
ci <- function(x) r*sin(th) + sqrt(r^2 - (x-r*cos(th))^2)
Q=1+1i*ci(1) ; pt(Q,'Q') ; seg(P,Q,col=8)
x=seq(0,1,0.01)
lines(x,ci(x),type='h',col=4)
pt(P/2,'r',cex=1.25)
#
area <- function(r,th){ # 円盤片の面積を算出
ci <- function(x) r*sin(th) + sqrt(r^2 - (x-r*cos(th))^2)
integrate(ci,0,1)$value
}
area=Vectorize(area)
# demo
area(1.146384,-pi/8)
th2r <- function(theta){ # θから円弧長を決定
r=uniroot(function(x) area(x,th=theta) - 1/2, c(1,2),tol=1e-24)$root #面積が1/2になるr
ci <- function(x) r*sin(theta) + sqrt(r^2 - (x-r*cos(theta))^2)
Q=1+1i*ci(1)
P=r*cos(theta)+1i*r*sin(theta)
r*bac(Q,P,0i)
}
th2r=Vectorize(th2r)
# demo
th2r(-pi/6)
x=seq(-pi/7,-pi/9, 0.0005)
plot(x,th2r(x),type='l',lwd=2,xlab=bquote(theta),ylab='円弧 OQ',cex.lab=1.25)
(opt=optimize(th2r,c(-pi/7,-pi/9),tol=1e-24))
uniroot(function(x) area(x,th=opt$minimum) - 1/2, c(1,2),tol=1e-24)$root # r
# 正方形の紙を頂点から切り始め、円周の一部（円弧）で面積を二等分するとき、
# 切り取り線の長さを出来るだけ短くするにはどうしたらよいか？
"
ガチャの確率問題
とあるソーシャルゲームのガチャにはN種類のキャラがいて、全て等確率で出てくる。
ｎ連ガチャを回したとき、どのキャラでもいいので同じキャラがｍ回以上出てくる確率を求めよ。"
"
mean(replicate(1e7,any(table(sample(N,n,rep=T))>=m)))
rm(list=ls())
options(digits=10)
source('toolmini.R')
plot(NULL,xlim=c(0,2),ylim=c(-1,1),asp=1,ann=F,axes=T)
O=0i;A=1+0i;B=1i;C=1+1i
pt(O,'O'); pt(A,'A') ; pt(B,'B') ; pt(C,'C')
seg(O,A);seg(0,B);seg(C,A);seg(C,B) ; seg(O,C,lty=3)
r=1.070437
th=-0.3647908 ; pt(0.15-0.025i,'θ') # Pの偏角
P=r*cos(th)+r*1i*sin(th) ; pt(P,'P(rcosθ,rsinθ)') ; seg(O,P,col=8)
Cir(P,r,col=8)
ci <- function(x) r*sin(th) + sqrt(r^2 - (x-r*cos(th))^2)
Q=1+1i*ci(1) ; pt(Q,'Q') ; seg(P,Q,col=8)
x=seq(0,1,0.005)
lines(x,ci(x),type='h',col=4)
pt(P/2,'r',cex=1.25) ; seg(O,C,lty=3)
"
integral r*sin(θ) + sqrt(r^2 - (x-r*cos(θ))^2) dx =
"
f <- function(x,r=1.070436,θ=-0.3647908) r*sin(θ) + sqrt(r^2 - (x-r*cos(θ))^2)
curve(f(x),0,1,add=T)
integrate(f,0,1)$value
Fn <- function(x,r=1.070436,θ=-0.3647908){
(1/2)*(x-r*cos(θ))*sqrt(r^2 - (x-r*cos(θ))^2) - (1/2)*r^2*atan((r*cos(θ)-x)/sqrt(r^2-(x-r*cos(θ)^2))) + r*x*sin(θ)
}
Fn(1)-Fn(0)
Area <- function(r,θ){
(1/2)*(1-r*cos(θ))*sqrt(r^2-(1-r*cos(θ))^2) - (1/2)*atan((r*cos(θ)-1)/sqrt(r^2+r*cos(θ)^2-1)) + r*sin(θ) +
(1/2)*r*cos(θ)*sqrt(r^2-r^2*cos(θ)^2) + (1/2)*r^2*atan(r*cos(θ)/sqrt(r^2+r*cos(θ)^2))
}
Area(r=1.070436,θ=-0.3647908)
「感染拡大は、Go to が原因とする科学的エビデンスはない」と自民党の連中が言うけどさ
ゴールデンウィーク前は「外出するな、旅行するな、帰省もするな」の大合唱だったんだよ。「人が移動したらウィルスも移動する」からね
それがいつの間にか、マスクして感染対策すりゃOK！ってなってるの何で？
#
https://www3.nhk.or.jp/news/special/coronavirus/data-all/ # 2019年の交通事故による死亡者の数は3215人、
https://www.nippon.com/ja/japan-data/h00625/ rm(list=ls())
x=2596 # new infection
r=1981 # culmutive death toll
n=130951 # culmutive infection
r/n # morality rate
x*r/n # estimated deaths in new infecton
ci=binom.test(r,n)$conf
data.frame(lower=ci[1]*x,upper=ci[2]*x)
d=365.2425
x*r/n*d # annual estimated
as.vector(x*ci*d)
x*r/n*d/3215 # ratio to traffic accident casul
as.numeric(x*ci*d/3215)
#
https://www3.nhk.or.jp/news/special/coronavirus/data-all/ # 2019年の交通事故による死亡者の数は3215人、
https://www.nippon.com/ja/japan-data/h00625/ rm(list=ls())
x=2596 # new infection
r=1981 # culmutive death toll
n=130951 # culmutive infection
r/n # morality rate
x*r/n # estimated deaths in new infection
ci=binom.test(r,n)$conf # 95% confidence interval(C.I.)
data.frame(lower=ci[1]*x,upper=ci[2]*x)
d=365.2425 # days in one-year
x*r/n*d # annual estimated
as.vector(x*ci*d) # 95%C.I.
x*r/n*d/3215 # ratio to traffic accident death casualities
as.numeric(x*ci*d/3215) # 95%C.I.
#
https://www3.nhk.or.jp/news/special/coronavirus/data-all/ # 2019年の交通事故による死亡者の数は3215人、
https://www.nippon.com/ja/japan-data/h00625/ rm(list=ls())
x=2596 # new infection
r=1981 # culmutive death toll
n=130951 # culmutive infection
r/n # morality rate
x*r/n # estimated deaths in new infection
ci=binom.test(r,n)$conf # 95% confidence interval(C.I.)
data.frame(lower=ci[1]*x,upper=ci[2]*x)
d=365.2425 # days in one-year
x*r/n*d # annual estimated
as.vector(x*ci*d) # 95%C.I.
ta=3215 # annual traffic accident fatality
x*r/n*d/ta # ratio to traffic accident fatality
as.vector(x*ci*d/ta) # 95%C.I.
#
https://www3.nhk.or.jp/news/special/coronavirus/data-all/ # 2019年の交通事故による死亡者の数は3215人、
https://www.nippon.com/ja/japan-data/h00625/ rm(list=ls())
x=2596 # new infection
r=1981 # culmulative death toll
n=130951 # culmulative infection
r/n # morality rate
x*r/n # estimated deaths in new infection
ci=binom.test(r,n)$conf # 95% confidence interval(C.I.)
data.frame(lower=ci[1]*x,upper=ci[2]*x)
d=365.2425 # days in one-year
x*r/n*d # annual estimated
as.vector(x*ci*d) # 95%C.I.
ta=3215 # annual traffic accident fatality
x*r/n*d/ta # ratio to traffic accident fatality
as.vector(x*ci*d/ta) # 95%C.I.
小選挙区制で（与党）議員どおしのcheck & balanceが消滅し、
内閣人事局で政治家と官僚のcheck & balanceが消滅。
制度化したのが民主党、制度を悪用したのが自民党。
その結果が
デフレ下に増税、
疫病下に旅行推進
という歴史に残る愚策。
小選挙区制で（与党）議員どおしのcheck & balanceが消滅し、
内閣人事局で政治家と官僚のcheck & balanceが消滅。
制度化に動いたのが民主党を作った政治家達、制度化して悪用したのが自民党。
その結果が
デフレ下に増税、
疫病下に旅行推進
という歴史に残る愚策。
財政破綻論を唱える連中には、この一言で全ての片が付く。
「日銀のFTF買い入れの財源教えて」
財政破綻論を唱える連中には、この一言で全ての片が付く。
「日銀のETF買い入れの財源教えて」
医師版になぜ統計？
俺、統計できるんだぜ
お前らと違って
あたまいいだろ
ホルホル、つうこと？
IMO <- function(x='IMO'){
y=unlist(strsplit(x,''))
n=length(y)
z=numeric(n)
for(i in 1:n) z[i]=which(y[i]==LETTERS)
w=z-1
sum(w*26^((n-1):0))+1
}
IMO('KINTAMA')
IMO('KKK')
pm=expand.grid(replicate(3,LETTERS,simplify=F))
pm=t(apply(pm,1,rev))
f <- function(x){
x[1]=='I' & x[2]=='M' & x[3]=='O'
}
which(apply(pm,1,f))
pm[5735,]
revLET <- function(x='IMO'){
y=unlist(strsplit(x,''))
n=length(y)
z=numeric(n)
for(i in 1:n) z[i]=which(y[i]==LETTERS)
z
}
revLET('IMO')
(9-1)*26^2+(13-1)*26+15
IMO <- function(x='IMO'){
y=unlist(strsplit(x,''))
n=length(y)
z=numeric(n)
for(i in 1:n) z[i]=which(y[i]==LETTERS)
w=z-1
sum(w*26^((n-1):0))+1
}
IMO('KINTAMA')
IMO('SEX')
IMO('YMO')
source('toolmini.R')
pm[12296,]
revLET("SEX")
dec2nw(12296,26,0)
n2IMO <- function(x){
y=dec2nw(x,26,0)+1
n=length(y)
y[n]=y[n]-1
print(paste(LETTERS[y],collapse = ''),quote=F)
}
n2IMO(2020)
１レスいくらだか知らねーけど、そんなバイトしなきゃならんほど困窮させた張本人擁護とかよくやるわ
IMO <- function(x){
y=unlist(strsplit(x,''))
n=length(y)
z=numeric(n)
for(i in 1:n) z[i]=which(y[i]==LETTERS)
w=z-1
sum(w*26^((n-1):0))+1
}
> IMO('CZR')
[1] 2020
n2IMO <- function(x){
r=x%%26
q=x%/%26
while(q > 0){
r=append(q%%26,r)
q=q%/%26
}
y=r+1
n=length(y)
y[n]=y[n]-1
print(paste(LETTERS[y],collapse = ''),quote=F)
}
> n2IMO(2020)
[1] CZR
中国の数字は信用できないと言われるが公文書改竄に賄賂五輪誘致GDPやらコロナやら数字誤魔化してる日本は言える立場に無い
ナースステーションの端で泣いている男性研修医(38)を見かけた時の適切な対応を１つ選べ。
a. 蹴り飛ばす
b. 抗うつ薬を処方する
c. 退職を勧める
d. 「サボっている研修医が居る」と院長へ報告する
これ本当に国試に出された問題なんだって。
ふざけるのもいい加減にしろと言いたいわ。
出題者のレベルが下がってるのは、やはり
学生の質が低下してるのと関係があるんだろうな。
しかし精神的に幼稚な出題者だよなｗ
出題者が一番、医師としての適性が欠けてるじゃんｗ
>>889 こういうのができないと金を毟り取られちゃう。
COVID19の潜伏期間の論文
https://www.nejm.org/doi/full/10.1056/NEJMoa2001316 結論は
#--- incubation period ---
# from Li et al NEJM 2020
# lognormal mean = 5.2
ln.par1 = 1.434065
ln.par2 = 0.6612
あるシリツ医が新型コロナ肺炎に罹患したとする。
行動調査によって発症前にキャバクラに行っており接客したキャバ嬢がシリツ医発症の２日後に発症していたことがわかった。
キャバ嬢はシリツ医から移されたと主張して１億円の賠償を求めている。
潜伏期間には幅がありキャバ嬢から移された可能性もあると主張してその確率を計算して賠償金を値切りたい。
いくら値切れるか計算せよ。
>>889 学部教員の声某
会議にて某教授曰く「統計できない人は進級させなくていいですから」
別の某教授からの怒りの電話：「基本的なことがわかっていない学生・大学院生が多い．教養部のうちにちゃんと教育してもらわないと！」
http://www.tmd.ac.jp/artsci/math/lec/tokunaga/statistics08_01.pdf 最終的には多くの学生が「わかってしまえば簡単だった」という感想を漏らします．
皆さんの先輩M君（現M４）の名言：「自転車と同じで，いったん乗れるようになればあとは楽々ですよ」
#
https://www3.nhk.or.jp/news/special/coronavirus/data-all/ # 2019年の交通事故による死亡者の数は3215人、
https://www.nippon.com/ja/japan-data/h00625/ rm(list=ls())
fn <- function(
x=2523, # new infection
r=2086, # culmulative death toll
n=142811 # culmulative infection
){
cat('mortality rate = ',r/n,'\n') # morality rate
cat('estimated deaths in newly infected = ',x*r/n,'\n') # estimated deaths in new infection
ci=binom.test(r,n)$conf # 95% confidence interval(C.I.)
print(data.frame(lower=ci[1]*x,upper=ci[2]*x))
d=365.2425 # days in one-year
cat('annual deaths estimated = ',x*r/n*d, '\n') # annual estimated
CI=as.vector(x*ci*d) # 95%C.I.
print(data.frame(lower=CI[1],upper=CI[2]))
ta=3215 # annual traffic accident fatality
cat('ratio to traffic accident fatality = ',x*r/n*d/ta,'\n') # ratio to traffic accident fatality
CI=as.vector(x*ci*d/ta) # 95%C.I.
print(data.frame(lower=CI[1],upper=CI[2]))
}
fn()
テレビのドキュメンタリーでやってたが
看護師が、これだけ働いて感染の危険も冒してるのにボーナス無しはあり得ないと病院側に訴え。
でも病院側は、利益が出なければボーナスなどとても出せない、経営が行き詰まってると。
実際私立病院ならそうだろう。
こういう医療現場こそコロナ補助で国が救済するべき。
なんで飲み屋や観光業など娯楽業種を助けるために
体張ってる医療機関を犠牲にするんだか。
あるドキュメンタリーでやってたが
看護師が、これだけ働いて感染の危険も冒してるのにボーナス無しはあり得ないと病院側に訴え。
でも病院側は、利益が出なければボーナスなどとても出せない、経営が行き詰まってると。
実際、私立病院ならそうだろう。
こういう医療現場こそコロナ補助で国が救済するべきと思う。
医療機関で適正な賃金を払えない現実こそ、医療崩壊だと思う。
生活圏を超える人の移動は、確実に接触率を上げ、これが実効再生産数を挙げて、感染者数上昇を引き起こす。
現在、GOTOでウィルスを全国に拡散中。
しばらくは、旅行を楽しむような若者や元気な人が隠れ陽性となり、これらが顕在化して爆増だな。
DR. FAUCI: You know, every single day we meet with the task force, and we take a look at what's going on.
And you don't want to make a pronouncement that no one should ever go into a restaurant.
I mean, I think that might be overkill right now, but everything is on the table.
It may come to the situation where we strongly recommend.
Right now, myself personally, I wouldn't go to a restaurant.
I just wouldn't because I don't want to be in a crowded place.
I have an important job to do.
I don't want to be in a situation where I'm going to be all of a sudden self-isolating for 14 days.
https://www.cbsnews.com/news/transcript-dr-anthony-fauci-discusses-coronavirus-on-face-the-nation-march-15-2020/ 安倍ぴょんまでも総合的・俯瞰的に粛清が始まってワクワクするのだが、朝敵安倍を撃ての詔が総理に下ったのかな？
桜を見る会でなく、前夜祭に焦点をあてているのは菅が無傷で安倍を撃ち落とすためだろうな。
桜を見る会そのものを取り上げると、スガもプリズン になってしまう。
バカはトリアージにより老人が追い出されると思って喜んでいたみたいだけど
現実には老人が優先されたというオチ
まあ若者はコロナで死なないけど老人はすぐ死んでしまうから
老人優先は当然なんだよなあ
感染者が入院希望しても入院できないのが医療崩壊だと思うのだが、現状は医療崩壊ではないのか？
感染者が入院希望しても入院できないのが医療崩壊だと思うのだが、現状は医療崩壊ではないのか？
あるシリツ医大で裏口入学率を推定したい。
何の情報もないのでその確率を0から1までの
>>488 一様分布とする。
調査により何人の裏口が続いたら裏口入学率の95%信頼区間の下限値が90%を超えるか？
そのときの裏口入学率の期待値はいくらか？
library(HDInterval)
f <- function(x) hdi(qbeta,0.95,shape1=1+x,shape2=1)
f=Vectorize(f)
n=0:100
y=f(n)
plot(n,(1+n)/(2+n),bty='l',ylab='Prob ',ylim=c(0,1),pch=19)
segments(n,y['lower',],n,y['upper',])
# points(n,y['lower',])
# points(n,y['upper',])
abline(h=0.90,col=8)
n0=uniroot(function(x,u0=0.90) f(x)[1] - u0, c(0,100))$root ; n0
(n0+1)/(n0+2)
(ceiling(n0)+1) / (ceiling(n0)+2)
k=1e3
oz=0.6/0.4
game <- function(x){
OZ=P=numeric()
OZ[x]=oz^(x-1)
P[x]=OZ[x]/(1+OZ[x])
rbinom(k,1,P[x])
}
sim <- function(a,b){
mean(game(a) > game(b))
}
sim(7,3)
海外からのコロナ流入を止めるのが遅すぎた 中国だけでなく欧州からの流入が続いたのが痛かった
検査の強化と隔離施設の手当が必要なのに、中国でそれが有効だったのを見ていたのに学ぶことなく折角クラスター対策で稼いだ時間を無駄にした
GoToキャンペーンはコロナが終息してから開始する約束だったのに反故にして前倒し実施して傷口を広げた
科学的根拠を重視せず思い付きで無意味な施策を繰り出した（一斉休校、アベノマスク、GoToキャンペーン）それもお友達利権つきで それらの施策は国会で審議もしていないから野党はどうすることもできないし、野党は桜を見る会だけ取り上げていたわけではない
少なくとも野党は「自民と同罪」ではない
君は結局自民のサポーターで、政府への批判が避けられないから野党も一緒だとレッテル貼りをしているのだろう
同じ島国なのに、支那ウィルスの抑え込みに成功した台湾とニュージーランド。
失敗した日本とイギリス。
この同じ島国であるながら、違いがなぜ生じたかを考えればわかる。
アベがFラン過ぎた。
ジョンソンも支那ウィルスを当初、極東の風土病くらいにしか思わず、対策を油断した。
一方台湾もNZも観光も主要産業だったが、1月に危機感を感じトップダウンで鎖国した。
島国の利点を生かし、外国からの人の流れを遮断し鎖国することで乗り切った。
1月、2月は経済が縮小したが、その成果が表れて現在は支那ウィルスを抑え込んだ。
今は国内の経済活動も解禁した。
それに比べて日本はどうだい？
アベは1月に全く危機感も持たず、「春節の支那人観光客のインバウンドを歓迎します。」と呑気なビデオメッセージを垂れ流してた。
アベは「非常事態宣言で鎖国する法的根拠がないー」とほざいて言い逃れする。
しかしアベにやる気があれば、総理大臣の伝家の宝刀「超法規的措置」が取れた。
日本赤軍がよど号をハイジャックし、刑務所の極左メンバーの釈放と、北チョン国への亡命を要求した。
当時の総理は、刑法、入管法も停止して、法秩序を捻じ曲げて、国交のない北チョン国に赤軍メンバーを亡命させた。
「超法規的措置」とはこのように強力な権力である。
しかしFラン大卒のアベは、1月に日本の鎖国…外人の入国禁止措置を取らなかった。
馬鹿のアベに危機感と責任感と決断力がなかった。
ま、1月の国会を「桜を見る会がー！」で無駄に貴重な時間を潰した糞ボケ野党どもも、痔民党と同罪だけどな。
日本にはろくな政党がない。
日本には”真の”保守政党が必要だ。
f <- function(
wAB=80, # Aの対B勝数
lAB=20, # Aの対B負数
wAC=30, # Aの対C勝数
lAC=20, # Aの対C負数
k=1e6){ # 乱数発生数
b=rbinom(k,wAB+lAB,lAB/(wAB+lAB)) # Bの勝数乱数
ba=b/(wAB+lAB-b) ; hist(ba,br='sc',fr=F) # Bのオッズ乱数
c=rbinom(k,wAC+lAC,lAC/(wAC+lAC)) # Cの勝数乱数
ca=c/(wAC+lAC-c) ; hist(ca,br='sc',fr=F) # Cのオッズ乱数
bc=ba/ca # Bの対Cオッズ乱数
summary(bc)
hist(bc,br='sc',fr=F)
Pbc=bc/(1+bc)
hist(Pbc)
summary(Pbc)
pbc=Pbc[!is.na(Pbc)]
print(summary(pbc))
plotPost(pbc,compVal = 0.5,showMode=T,showCurve = T,xlab='Prob[B beats C]')
hdi(pbc)
}
library(gmp)
f <- function(N){
a=factorialZ(N)
b=as.character(a)
c=as.numeric(unlist(strsplit(b,'')))
d=rev(c)
if(d[1]!=0) return(NA)
else return(rle(d)$values[2])
}
N=1:1000
y=sapply(N,f)
plot(N,y,bty='n')
z=data.frame(N,digit=y)
head(z,10)
tail(z,10)
library(gmp)
f <- function(N){
a=factorialZ(N)
b=as.character(a)
c=as.numeric(unlist(strsplit(b,'')))
d=rev(c)
if(d[1]!=0) return(NA)
else return(rle(d)$values[2])
}
N=1:10004
y=sapply(N,f)
plot(N,y,bty='n')
z=data.frame(N,digit=y)
head(z,10)
tail(z,10)
a=z[-1:-4,] # non-zero digit
b=vector('list',length=9)
for(i in c(2,4,6,8)){
b[[i]]=a[a$digit==i,]$N
}
b
c=sapply(c(2,4,6,8), function(i) length(b[[i]]))
data.frame(digit=c(2,4,6,8),個数=c)
# 差X-Yのpdfの公式
# ∫[-∞,∞] pdf1(x+y)*pdf2(y) dy
# x ~ pdf1,y ~ pdf2から x-y のpdfを返す
pdf_minus <- function(pdf1,pdf2){
f <- function(x,y) pdf1(x+y)*pdf2(y)
f=Vectorize(f,vectorize.args = 'y')
pdf <- function(x)
integrate(function(y) f(x,y),-Inf,Inf,rel.tol=1e-14)$value
pdf=Vectorize(pdf)
invisible(pdf)
}
# ex. COVID19 incubation time
mu = 1.434065 ; sg = 0.6612
x=rlnorm(1e6,mu,sg) ; y=rlnorm(1e6,mu,sg)
hist(x-y,xlim=c(-30,30),freq=F,breaks=250,lty=1,col='skyblue',main='')
pdf_minus(function(x)dlnorm(x,mu,sg),
function(x)dlnorm(x,mu,sg)) -> pdf
curve(pdf(x),add=T)
var=integrate(function(x) x^2*pdf(x),-Inf,Inf)$value
sqrt(var)
integrate(pdf,2,Inf,rel.tol=1e-12)
mean(x-y>2)
library(polspline)
fit=logspline(x-y)
curve(dlogspline(x,fit),add=T,col=4)
1-plogspline(2,fit)
日本の誇り
★亀井静香
「簡単に言いますと・・・
小泉・竹中改革と称する路線の逆をやれば日本の未来が開かれる、
このように私は思います。」
ダウンロード＆関連動画＞＞
@YouTube;t=350s
たちが悪いのは同じような派遣会社がゴキブリ並に増えたことだね。起業したやつの8割以上が派遣会社って狂ってる。派遣会社が増えると単価も質も下がるからいいことなんてない。少なくとも正社員派遣なんて社員1000人未満の企業がやることじゃない。
一国の総理がイの1番に逃げ出すんやから、それから比べりゃ残ってる医療従事者は神だな
こういうのができないと金を毟り取られちゃうから、統計は臨床医には必須。
COVID19の潜伏期間の論文
https://www.nejm.org/doi/full/10.1056/NEJMoa2001316 結論は
#--- incubation period ---
# from Li et al NEJM 2020
# lognormal mean = 5.2
ln.par1 = 1.434065
ln.par2 = 0.6612
ある開業医が新型コロナ肺炎に罹患したとする。
行動調査によって発症前にキャバクラに行っており接客したキャバ嬢が開業医発症の２日後に発症していたことがわかった。
キャバ嬢は開業医から移されたと主張して１億円の賠償を求めている。
潜伏期間には幅がありキャバ嬢から移された可能性もあると主張してその確率を計算して賠償金を値切りたい。
いくら値切れるか計算せよ。
うりゅうひろゆきの本スレにようこそ！
このウンコスレは基本的にさらしアゲて使用します！
ココは医師真似事務員ジイさんが、医師ねたみの挙句、テメェで勝手に自称で医科歯科大を卒業した医師って設定で
妄想願望日記を発表するスレです
お医者さんのマトモなレスなど全く不要！
ゴミ箱まがいの公衆便所掃き溜め痰壷下品スレとして使用しましょうね
そんなわけで、いまだ懲りない恥さらし（自称）医科歯科事務員ジジイ登場～～
│ 彡川川川三三三ミ～ プウゥ～ン
｜ 川｜川／ ＼｜～ ポワ～ン ＿＿＿＿＿＿＿＿
｜ ∥｜∥ ◎---◎｜～ ／
｜ 川川∥ 3 ヽ～ ＜ 僕はうりゅうひろゆき
｜ 川川 ∴）д（∴）～ ＼＿＿＿＿＿＿＿＿
｜ 川川 ～ /～ カタカタカタ
｜ 川川∥ ～ /∥ ＿＿＿＿＿
｜ 川川川川＿＿＿／∥ | |￣￣＼ ＼
｜ ／ ＼＿＿| | |￣￣|
｜ / ＼医科歯科 | | |＿＿|
｜ | ＼ |つ |＿_|＿＿／ ／
｜ / 医師うらやましいぜ・・ |￣￣￣￣| 〔￣￣〕
よし、医科歯科の医者と称して
私立のお医者様を攻撃だ！なんたって、医科歯科の看板借りてんだからな
え？証明？？？自称だから医科歯科の学生証、卒業証書あるわけねえよ
同期の医師あげてみろ、ったて、そもそも医師じゃねえし居ねえよバカ
でも病院でもらった、医科歯科の封筒はもってま～す！これを証拠にしてやるぜ
専門医？欲しいけど・・いいや！そんなの必要ねえ！ 俺は事務員だし
本日のニュー速＋より
452 ニューノーマルの名無しさん 2020/12/03(木) 11:45:56.01 ID:ChAQFKI00
近大病院とか大丈夫かよ
バカ大卒の医者の集団だろ
国家試験も通らないウリュウの馬鹿がなんか言ってるw
国家試験合格してないのに国家試験は簡単だと嘯く万年浪人生、社会の底辺の分際で。
ibrary(fmsb)
"
GOTOトラベルだと
40,000,000 / 172 = 232,558人に一人感染
日本の人口12600万/感染者15万=840人に一人感染
GOTOトラベル参加は新コロナ感染リスクを何分の１に減らすことができるか？
95%信頼区間付きで計算せよ。
"
riskratio(172,15e4,4000e4,12600e4)
rateratio(172,15e4,4000e4,12600e4)
1/riskratio(172,15e4,4000e4,12600e4)$conf
1/riskratio(172,15e4,4000e4,12600e4)$est
桜の会は安倍自身も完全アウトだね
たとえば初めて発覚した事件で
｢秘書が勝手にやってましたー｣的なトカゲのしっぽ切りはよくあるけど、
今回の件は、すでに国会で国民の前で追及議論されていた問題であって
その国会を通して、安倍総理は国民に対して、自身が責任を持って確認した上で
「明細はない」｢補填は一切ない｣｢全て参加者個人で支払ってる｣と安倍自身が明言してたんだからな…
結果、｢確認した上で｣国会で嘘をつきまくって、その時の議論追求を逃れていたんだから、これは秘書ガー案件では通らない
安倍自身も完全にアウト・・
ウリュウによるウリュウのためのクソスレ
ウリュウとは？
長年この板に執着する、私立医学部を僻みまくる自称医科歯科卒の万年浪人生。5chに毎日恨み言を書くしか人生の楽しみがない可哀想な人。
シリツ医は>927の計算もできないのはなぜか？
裏口だから。
飲食店の店内飲食はコロナ拡大を助長・・アメリカの複数の大学の研究結果
https://forbesjapan.com/articles/detail/38240 レストランの営業再開と新型ウイルスの感染拡大との明らかな相関関係を総括的に示した最初の研究結果は6月、ジョンズ・ホプキンス大学により発表された。
同大は米国内3000万人のクレジットカード利用データを分析し、各州での流行状況との関係を調査。
結果、レストランの利用が増えるほど感染も増加していたことが明白に示された。
飲食業が直面している問題は、衛生管理などの対策にまつわるものではなく、私たちには対処のしようがない「スーパースプレッダー」の存在だ。
同じレストラン内にスーパースプレッダーが1人存在すれば、感染の可能性は非常に高まる。
それは、QRコードのメニューを導入し、消毒ジェルを常備し、スタッフにマスクの常時着用を義務付けるなどの感染対策を万全にしても同じだ。
つまり、店側は感染を防ぐことができないのだ。
スタンフォード大の研究結果は、レストラン経営者にとって最悪のニュースだ。
飲食業は経済で大きな役割を担っているが、現時点では感染拡大を抑制するためにテイクアウトのみの営業に制限するほかないことを、私たちは受け入れなければいけない。
テイクアウトのみの営業でも、徹底した衛生管理は必要になる。
これまでに蓄積されてきた証拠やデータ、科学的研究結果は疑いの余地がない。
残念ながら、ワクチンが普及するまでは、レストランやバーを閉店するのが唯一の責任ある対処法になる。
医師ならば大事な仕事があるから小金につられて外食しないよ。
ファウチ博士
「私はレストランには行かない」
「大切な仕事があるから」
DR. FAUCI: You know, every single day we meet with the task force, and we take a look at what's going on.
And you don't want to make a pronouncement that no one should ever go into a restaurant.
I mean, I think that might be overkill right now, but everything is on the table.
It may come to the situation where we strongly recommend.
Right now, myself personally, I wouldn't go to a restaurant.
I just wouldn't because I don't want to be in a crowded place.
I have an important job to do.
I don't want to be in a situation where I'm going to be all of a sudden self-isolating for 14 days.
医師ならば大事な仕事があるから小金につられて外食しないよ。
ファウチ博士
「私はレストランには行かない」
「大切な仕事があるから」
DR. FAUCI: You know, every single day we meet with the task force, and we take a look at what's going on.
And you don't want to make a pronouncement that no one should ever go into a restaurant.
I mean, I think that might be overkill right now, but everything is on the table.
It may come to the situation where we strongly recommend.
Right now, myself personally, I wouldn't go to a restaurant.
I just wouldn't because I don't want to be in a crowded place.
I have an important job to do.
I don't want to be in a situation where I'm going to be all of a sudden self-isolating for 14 days.
https://news.yahoo.com/myself-personally-wouldnt-restaurant-fauci-174014267.html "
ある国では人々は生まれてくる子には男の子だけを欲しがりました。
そのため、どの家族も男の子を産むまで子供を作り続けました。
この国では男の子と女の子の人口比率はどうなりますか？
人間の出生性比は地域、時代にかかわらず男女がおおむね105:100前後である。
https://ja.wikipedia.org/wiki/%E6%80%A7%E6%AF%94 "
sim <- function(){
mf=numeric()
baby=sample(1:0,1,prob=c(p,1-p))
mf=baby
while(baby!=1){
baby=sample(1:0,1,prob=c(p,1-p))
mf=c(mf,baby)
}
mf
}
k=1e6
mf=unlist(replicate(k,sim()))
mean(mf) ; p
m=sum(mf)
f=length(mf)-sum(mf)
m/f
p=105/205
q=1-p
p/q
n=1e5
m <- function(n){ # p*(1+q+q^2+q3+q^4+...)
re=0
for(i in 1:n) re = re + q^(i-1)*p
re}
f <- function(n){
re=0
for(i in 1:n) re = re + i*q^i*p
re}
m(n)/f(n)
検査希望者が自主的に検査を受けて検査数を増やすやり方では、
いくら検査数が増えても効果が少ないのは、
アメリカや欧州を見てあきらか
おそらく高リスク群なのに検査受けない人が多いんでしょう
中国方式で検査数を増やすのがいちばん確実で効果がある
この地域で〇〇業種で働いてるやつ全員検査うけろ、
とか、この地域の住民全員検査受けろ、
とか、この工場で働いてるやつ全員検査、この学校のやつ全員検査、
みたいに、行政が検査対象を指定して1人も逃さず検査することが重要
米国が移民政策成功してるのって弱者が病気になろうと
気にせずゴミのように放置できるから社会コストが跳ね上がらないからだろう。
日本は多民族共生できるほど民度が高くないんだよなぁ。
日本だと気の毒だからと国保にタカらせ集中治療室まで使わせるからパンクする
米国が移民政策成功してるのって弱者が病気になろうと
気にせずゴミのように放置できるから社会コストが跳ね上がらないからだろう。
日本は多民族共生できるほど民度が高くないんだよなぁ。
日本だと気の毒だからと国保にタカらせ集中治療室まで使わせるからパンクする
★亀井静香
「簡単に言いますと・・・
小泉・竹中改革と称する路線の逆をやれば日本の未来が開かれる、
このように私は思います。」
ダウンロード＆関連動画＞＞@YouTube;t=350s
１０００年に一度の大地震と日本初の原発メルトダウンに同時に対処した民主党政権
今年３度目の感染拡大期を迎えてもまともに感染防止策をうてない自民党政権
こう書くと菅直人って実はずげぇ優秀だったんじゃねーかと思えてくる
うりゅうひろゆきの本スレにようこそ！
このウンコスレは基本的にさらしアゲて使用します！
ココは医師真似事務員ジイさんが、医師ねたみの挙句、テメェで勝手に自称で医科歯科大を卒業した医師って設定で
妄想願望日記を発表するスレです
お医者さんのマトモなレスなど全く不要！
ゴミ箱まがいの公衆便所掃き溜め痰壷下品スレとして使用しましょうね
そんなわけで、いまだ懲りない恥さらし（自称）医科歯科事務員ジジイ登場～～
│ 彡川川川三三三ミ～ プウゥ～ン
｜ 川｜川／ ＼｜～ ポワ～ン ＿＿＿＿＿＿＿＿
｜ ∥｜∥ ◎---◎｜～ ／
｜ 川川∥ 3 ヽ～ ＜ 僕はうりゅうひろゆき
｜ 川川 ∴）д（∴）～ ＼＿＿＿＿＿＿＿＿
｜ 川川 ～ /～ カタカタカタ
｜ 川川∥ ～ /∥ ＿＿＿＿＿
｜ 川川川川＿＿＿／∥ | |￣￣＼ ＼
｜ ／ ＼＿＿| | |￣￣|
｜ / ＼医科歯科 | | |＿＿|
｜ | ＼ |つ |＿_|＿＿／ ／
｜ / 医師うらやましいぜ・・ |￣￣￣￣| 〔￣￣〕
よし、医科歯科の医者と称して
私立のお医者様を攻撃だ！なんたって、医科歯科の看板借りてんだからな
え？証明？？？自称だから医科歯科の学生証、卒業証書あるわけねえよ
同期の医師あげてみろ、ったて、そもそも医師じゃねえし居ねえよバカ
でも病院でもらった、医科歯科の封筒はもってま～す！これを証拠にしてやるぜ
専門医？欲しいけど・・いいや！そんなの必要ねえ！ 俺は事務員だし
在日米軍が先手先手をうってきた。
半径150キロは会食禁止
東京神奈川千葉の密集地帯は立ち入り禁止。
誰も突っ込まないけど、自民が増長したここ１０年で
国会答弁の新機軸ルール確立しちゃったの気付いてる？
「仮定の話にはお答えできません」 （事実上の答弁拒否ｗ同じ質問を再度されても繰り返しで逃げ切りＯＫｗ）
「各種事情を勘案して総合的に判断しました」（その総合的判断の具体的な説明を再度求められてもこの繰り返し）
「個別の案件にお答えする事は差し控えさせて頂きます」 （逆に個別の案件でない案件って何？w）
「そもそも」コレがまかり通るなら世の中に存在する事案の９９％、これで答弁回避できちゃうんだよなｗ
でも誰もソレに突っ込まずにこれが「責任もって誠実に真摯に回答した」でまかり通ってる異常さw
都合の悪い事案になったらこのやり取りの無限ループを聞かされるだけｗ事実もうそうなってるw
一応答弁したよｗってな既成事実作りの為に「あくまで一般論としてお答えさせて頂きますと～」だのテンプレ喚いて強制終了ｗ
安倍からの流れで菅も異常に多いんだよねこのテンプレ回答、もう固定文法表現みたいになってるのな
「～により回答はは差し控えさせて頂きます～いずれにしましても一般的には～」
この様式の繰り返し
更にテンプレフレーズに「人事の事なので回答は差し控えます」が堂々追加ッ！！ウエーイw
マジ終わってるよこの国w
米国立アレルギー感染症研究所（NIAID）のアンソニー・ファウチ所長は
新型コロナウイルスの感染拡大を食い止めるには学校ではなくバーやレストランの閉鎖が必要と主張している。
ABCニュースの取材に応じた中で発言した。
ファウチ所長はABCニュースの取材に応じた中で「学校ではなくバーを閉鎖すべき」と発言した。
ファウチ所長によれば、学校に通う子供たちの安全を確保するには、教育機関の閉鎖ではなく市中感染レベルを低く維持する必要があるという。
この意味において大きな脅威となるのが、マスクを着用せずに飲食するレストランやバーの存在としている。
https://jp.sputniknews.com/covid-19/202011307977386/ 【コロナ感染リスク高い場所】断トツ「レストラン」会食リスク 9800万人のデータで判明…尾身会長「飲食店での感染きわめて多い」★３
http://2chb.net/r/newsplus/1606956739 自称医科歯科卒の医師コンプまみれの哀れな社会の底辺くん。
GOTOトラベル GOTOイートも
完全に 現場で苦労している医療従事者を愚弄する行為
現場の医療のプロには、感染してはいけないと言って
旅行や外食や帰郷は控えさせ、病院の寄宿舎に泊まらせ
かつボーナスは減らし 感染の恐怖と過重労働で煮え湯を飲ませ
院内感染はプロのくせに感染するなどけしからんと報道し
かたや一般人には税金注いで 遊びまわって外食や旅行を奨励し
しかも患者を増やし、医療従事者の負担を増やす
医療従事者に暴動が起きないほうがおかしいくらい
シリツ医は>927の計算もできないのはなぜか？
裏口だから。
まー白々しい。毎回毎回同じ言葉しか言わないのに。匿名だからバレないとでも？
さすが非医だね。
うちは、かかりつけの老人は時間外でも診ているけど
一見さんの若者はお断りだな。
まあ若者はコロナで死なないけど老人はすぐ死んでしまうから
老人優先は当然。
将来ある世代こそ自粛要請すべき。
比率の検定すらできないのがシリツ医
だって、裏口ですもの。
"
GOTOトラベルだと
40,000,000 / 172 = 232,558人に一人感染
日本の人口12600万/感染者15万=840人に一人感染
GOTOトラベル参加は新コロナ感染リスクを何分の１に減らすことができるか？
95%信頼区間付きで計算せよ。
"
>>959 やはり、計算できない裏口シリツだな。
他スレでも正論が
>>880 だって、私立医ダモン ばかだもん
この板に非医って可哀想。
だってずっと医者コンプでこんなところでしか発散できないんだから。
ここの板では医師免許持ってるかどうかが全てなので。
あ、誰とは言わないけど自称医科歯科は非医なので悪しからず。笑
これ！
不朽の名投稿
>>
私は昭和の時代に大学受験したけど、昔は今よりも差別感が凄く、特殊民のための特殊学校というイメージで開業医のバカ息子以外は誰も受験しようとすらしなかった。
常識的に考えて、数千万という法外な金を払って、しかも同業者からも患者からもバカだの裏口だのと散々罵られるのをわかって好き好んでド底辺医に行く同級生は一人もいませんでした。
本人には面と向かっては言わないけれど、俺くらいの年代の人間は、おそらくは８－９割はド底辺医卒を今でも「何偉そうなこと抜かしてるんだ、この裏口バカが」と心の底で軽蔑し、嘲笑しているよ。
当の本人には面と向かっては絶対にそんなことは言わないけどね。
<<
東京医大の事件は裏口入学が現在進行形であること如実にしめした事件だよね。
シリツ医の使命は裏口入学撲滅国民運動の先頭に立つことだよ。
裏口入学の学生を除籍処分にしないかぎり、信頼の回復はないね。つまり、いつまで経ってもシリツ医大卒＝裏口バカと汚名は拭えない。シリツ出身者こそ、裏口入学に厳しい処分せよを訴えるべき。
裏口入学医師の免許剥奪を！の国民運動の先頭に立てばよいぞ。
僕も裏口入学とか、言ってたら信頼の回復はない。
コピペと統計しか脳のないウリュウじいさん。
医者なんか到底勤まりませんね。
残念ながら東京医科大学出身のお医者様>>(超えられない壁)>>非医が世間一般の考え。これが現実。
>>965 俺、国立卒だから>958の計算できるよ。
裏口シリツ医には無理。
ド底辺シリツ医の三法則
一、ド底辺シリツ医大が悪いのではない、本人の頭が悪いんだ。
二、ド底辺シリツ医大卒は恥ずかしくて、学校名を皆さま言いません。
三、ド底辺シリツ医大卒は裏口入学の負い目から裏口馬鹿を暴く人間を偽医者扱いしたがる。
>>968 俺国立医学部医学科卒
あんたは？どうせ医科歯科なんでしょ？非医の
>>969 国立卒で>958の計算ができないのはおかしいから
裏口シリツ医だろうな。
rm(list=ls())
source('toolmini.R')
r=1
x=seq(-1,259/880,0.005)
y=sqrt(r^2-x^2)
plot(x,y,xlim=c(-1,5),ylim=c(-2,2),asp=1,type='n',col=3,axes=F,ann=F)
# points(x,-y,col=3,type='h')
Cir(0i,1)
R=1.25
A=1.1
Cir(A+0i,R)
seg(259/880-1i*(3*sqrt(78591))/880,259/880+1i*(3*sqrt(78591))/880)
"
x^2+y^2=1
(x-1.1)^2+y^2=1.25^2
x = 259/880 ∧ y = +(3 sqrt(78591))/880
x = 259/880 ∧ y = -(3 sqrt(78591))/880
"
pt(-0.5+0i,'A')
pt(0.1+0i,'B')
pt(0.5+0i,'C')
pt(1.25+0i,'D')
>>969 俺は二期校時代の入学だから、医学部看護学科なんてなかったぞ。
>>971 二次元で面積1のシャボン玉と面積2のシャボン玉が合体した時に
表面張力で最終的にどんな形に落ち着くか
医師免許持ってないくせに偉そうだなw
二期とかいつの時代のジジイだよ。
rm(list=ls())
source('toolmini.R')
r=1
x=seq(-1,259/880,0.005)
y=sqrt(r^2-x^2)
plot(x,y,xlim=c(-1,5),ylim=c(-2,2),asp=1,type='h',col=3,axes=F,ann=F)
points(x,-y,col=3,type='h')
lines(x,y,lwd=3) ; lines(x,-y,lwd=3)
R=1.25
A=1.1
x=seq(259/880,2.35,0.005)
y=sqrt(R^2-(x-A)^2)
points(x,y,col=2,type='h')
points(x,-y,col=2,type='h')
lines(x,y,lwd=3) ; lines(x,-y,lwd=3)
seg(259/880-1i*(3*sqrt(78591))/880,259/880+1i*(3*sqrt(78591))/880,col=4,lwd=5)
"
x^2+y^2=1
(x-1.1)^2+y^2=1.25^2
x = 259/880 ∧ y = +(3 sqrt(78591))/880
x = 259/880 ∧ y = -(3 sqrt(78591))/880
"
大学受験で時間が止まってる万年受験生の非医は今の医療現場なんか知るわけないもんな。医者になった人たちにとって統計だの数学だの何年前の話？っていうことだ
もうずっとここの板に粘着して誰一人相手にしてくれなかったんだろ？きっと数え切れないほどの医者に誰にも相手にされなかったということは少なくともお前のことなんか道端のゴミみたいな存在だったということ。
それを教えてやってるだけ感謝しろ。
この前医学部新設されたばかりだよな？学費も数千万。
どれだけ僻んでも医学部は国立だけにはならない。
こんなところで騒ぐしか能のない非医と違って未来の医者が日本に必要とされてるんだよ。残念だったな。
うりゅうひろゆきの本スレにようこそ！
このウンコスレは基本的にさらしアゲて使用します！
ココは医師真似事務員ジイさんが、医師ねたみの挙句、テメェで勝手に自称で医科歯科大を卒業した医師って設定で
妄想願望日記を発表するスレです
お医者さんのマトモなレスなど全く不要！
ゴミ箱まがいの公衆便所掃き溜め痰壷下品スレとして使用しましょうね
そんなわけで、いまだ懲りない恥さらし（自称）医科歯科事務員ジジイ登場～～
│ 彡川川川三三三ミ～ プウゥ～ン
｜ 川｜川／ ＼｜～ ポワ～ン ＿＿＿＿＿＿＿＿
｜ ∥｜∥ ◎---◎｜～ ／
｜ 川川∥ 3 ヽ～ ＜ 僕はうりゅうひろゆき
｜ 川川 ∴）д（∴）～ ＼＿＿＿＿＿＿＿＿
｜ 川川 ～ /～ カタカタカタ
｜ 川川∥ ～ /∥ ＿＿＿＿＿
｜ 川川川川＿＿＿／∥ | |￣￣＼ ＼
｜ ／ ＼＿＿| | |￣￣|
｜ / ＼医科歯科 | | |＿＿|
｜ | ＼ |つ |＿_|＿＿／ ／
｜ / 医師うらやましいぜ・・ |￣￣￣￣| 〔￣￣〕
よし、医科歯科の医者と称して
私立のお医者様を攻撃だ！なんたって、医科歯科の看板借りてんだからな
え？証明？？？自称だから医科歯科の学生証、卒業証書あるわけねえよ
同期の医師あげてみろ、ったて、そもそも医師じゃねえし居ねえよバカ
でも病院でもらった、医科歯科の封筒はもってま～す！これを証拠にしてやるぜ
専門医？欲しいけど・・いいや！そんなの必要ねえ！ 俺は事務員だし
川崎医大の創始者の子供や孫は教育投資して学力をつけて
岡山大学や京都大学の医学部に入学。
法外な学費が払える経済状況にありながらド底辺シリツ医大にしか入れないのは馬鹿の証明。
僕も裏口入学と公言したシリツ医は比例計算すら間違える。
https://news.yahoo.co.jp/articles/5a507fc8250323400d786f70d75d512d81e32ef4 D=E=numeric()
D[1]=190
E[1]=D[1]
# D[2]=E[1]%/%5
# E[2]=D[2]+E[1]%%5
i=1
while(E[i]>5){
D[i+1]=E[i]%/%5
E[i+1]=D[i+1]+E[i]%%5
i=i+1
}
sum(E)
r=1
x=seq(-1,259/880,0.005)
y=sqrt(r^2-x^2)
plot(x,y,xlim=c(-1,3),ylim=c(-2,2),asp=1,type='n',col=3,axes=F,ann=F)
points(x, y,col=3,type='h')
points(x,-y,col=3,type='h')
lines(x,y,lwd=1) ; lines(x,-y,lwd=1)
R=1.25
A=1.1
x=seq(259/880,R+A,0.005)
y=sqrt(R^2-(x-A)^2)
points(x,y,col=2,type='h')
points(x,-y,col=2,type='h')
lines(x,y,lwd=1) ; lines(x,-y,lwd=1)
pt(0i,'O')
abline(h=0,lty=3)
o=0i
a=A+0i
pt(a,'A')
b=259/880+(3i*sqrt(78591))/880
pt(b,'B')
seg(o,b)
pt(0.1+0.1i,quote(theta),cex=1.5)
seg(a,b)
pt(o/2+b/2,'r',cex=1.5)
pt(a/2+b/2,'R',cex=1.25)
Cir(o,r,lty=3)
Cir(a,R,lty=3)
>>982 ド底辺シリツ医大を擁護するなんてド底辺シリツ医大卒だろうな。
シリツ医のこれが現実
１次方程式もできないド底辺特殊シリツ医大卒の記録
何度読んでも馬鹿すぎる。
男女別の割合と全体での割合から男女比が計算できるとも思わないとは。
なんでこんなのが大学に入れるわけよ？
裏口入学以外に説明がつく？
中学生でも解ける一次方程式の問題だろ。
それすらできない馬鹿が自信を持って発言。
>患者の男女比が必要なのもわからないのか？
だとさ。
0.2575549
と答を書いてやったら
>単位も書かずに答えだとか…
ド底辺シリツ医大では確率に単位があるらしいぞw
何でこんな馬鹿が大学に入れるわけ？
裏口入学以外に説明がつく？
f <- function(n190=190,n5=5){
D=E=numeric()
D[1]=n190
E[1]=D[1]
i=1
while(E[i]>=n5){
D[i+1]=E[i]%/%n5
E[i+1]=D[i+1]+E[i]%%n5
i=i+1
}
sum(D)
}
f=Vectorize(f)
f(1e6)
"
問題）１００万本のジュースがあります。このジュースの空き瓶5本と同じジュース一本が交換できます。この交換をくり返しながら
ジュースが全部なくなるまで飲みました。全部で何本飲めたでしょうか？
"
rm(list=ls())
options(digits=22)
f <- function(n190=190,n5=5){
D=E=numeric()
D[1]=n190
E[1]=D[1]
i=1
while(E[i]>=n5){
D[i+1]=E[i]%/%n5
E[i+1]=D[i+1]+E[i]%%n5
i=i+1
}
sum(D)
}
f=Vectorize(f)
f(1e6)
n=1:1000
y=f(n)
plot(n,y,type='l')
lm(y~n)
ド底辺シリツ医にはこれは解けないと思う。
問題の意味は小学生でもわかる。
問題）
1本100円のジュースがあります。
このジュースの空き瓶5本と同じジュース一本が交換できます。
手元に100万円あります。
(1)何本買う時が一本あたりの単価がもっとも安くなりますか？
(2)そのとき何本飲めるでしょうか？
こんな朝っぱらから7連続書き込みで発狂か。
そうやって一生お医者様僻んでここで発狂して終わるのか。惨めな人生だな。
rm(list=ls())
options(digits=22)
f <- function(n190=190,n5=5){
D=E=numeric()
D[1]=n190
E[1]=D[1]
i=1
while(E[i]>=n5){
D[i+1]=E[i]%/%n5
E[i+1]=D[i+1]+E[i]%%n5
i=i+1
}
sum(D)
}
f=Vectorize(f)
uniroot(function(x,u0=1000) f(x)-u0, c(500,1000))
呼吸苦の旅行客で救急収容の依頼。
1万円のインセンティブが当直代に加算されるけど、小金につられてリスクを背負うのはＧＯＴＯ乞食と同じになるので対応不能とお断りした。
そのかわりというわけでもないが、地元住民の軽症救急搬送を経過観察入院させてインセンティブＧＥＴ！
>>994 週３日午前中だけ。
昔とった杵柄で麻酔やCSの内視鏡バイトに行ってたけど
今は診断EGDバイトのみにした。
金に釣られてリスクを負いたくなくなったので。
エパデール内服でも抗血小板薬内服なので観察のみで生検不可がバイト先でのルール。
前日にサバ缶食っても生検不可になんのかよ？と思いながらもルールにはしたがっている。
君子危うきに近寄らず。
裏口シリツ医ってある意味すごいよなぁ
常識的に考えて、数千万という法外な金を払って、しかも同業者からも患者からもバカだの裏口だのと散々罵られるのをわかって好き好んでド底辺医というスティグマを買うわけだから。
Last but not least, three laws of Do-Teihen Medical School, currently called Gachi'Ura by its graduates.
最後にド底辺医大の三法則を掲げましょう。
1: It is not the bottom medical school but its enrollee that is despicable, which deserves to be called a bona fide moron beyond redemption.
ド底辺シリツ医大が悪いのではない、本人の頭が悪いんだ。
2: The graduates of Do-Teihen are so ashamed that none of them dare to mention their own alma mater which they have gone through.
ド底辺シリツ医大卒は恥ずかしくて、学校名を皆さま言いません。
3: The Do-Teihen graduates are so ashamed of having bought their way into the exclusively bottom-leveled medical school
that they tend to call a genuine doctor a charlatan who elucidates their imbecility.
ド底辺シリツ医大卒は裏口入学の負い目から裏口馬鹿を暴く人間を偽医者扱いしたがる。
前々スレからのド底辺シリツ医への宿題
若い女性研修医（嘘つきかどうかは不明）から
「あなたのいうことが正しければ手コキかフェラをしてあげる、そうでなければセンズリを命じる」と言われた。
フェラをしてもらうには何と言えばいいか？
答だせないってアホなの？
フェラよりセンズリが好きなの？
Last but not least, three laws of Do-Teihen Medical School, currently called Gachi'Ura by its graduates.
最後にド底辺医大の三法則を掲げましょう。
1: It is not the bottom medical school but its enrollee that is despicable, which deserves to be called a bona fide moron beyond redemption.
ド底辺シリツ医大が悪いのではない、本人の頭が悪いんだ。
2: The graduates of Do-Teihen are so ashamed that none of them dare to mention their own alma mater which they have gone through.
ド底辺シリツ医大卒は恥ずかしくて、学校名を皆さま言いません。
3: The Do-Teihen graduates are so ashamed of having bought their way into the exclusively bottom-leveled medical school
that they tend to call a genuine doctor a charlatan who elucidates their imbecility.
ド底辺シリツ医大卒は裏口入学の負い目から裏口馬鹿を暴く人間を偽医者扱いしたがる。
-curl
lud20241203085734ca
このスレへの固定リンク： http://5chb.net/r/hosp/1592215787/ヒント：5chスレのurlに
http://xxxx.5ch
b.net/xxxx のように
bを入れるだけでここでスレ保存、閲覧できます。
TOPへ TOPへ
全掲示板一覧 この掲示板へ 人気スレ |
>50
>100
>200
>300
>500
>1000枚
新着画像
↓「底辺私立医大を卒業した医者って頭悪いよね？ Part17 YouTube動画>24本 ->画像>89枚 」を見た人も見ています：
・底辺私立医大を卒業した医者って頭悪いよね？ Part20
・底辺私立医大を卒業した医者って頭悪いよね？ Part21
・底辺私立医大を卒業した医者って頭悪いよね？ Part16
・底辺私立医大を卒業した医者って頭悪いよね？ Part23
・底辺私立医大を卒業した医者って頭悪いよね？ Part9
・底辺私立医大を卒業した医者って頭悪いよね？ Part6
・底辺私立医大を卒業した医者って頭悪いよね？ Part12
・底辺私立医大を卒業した医者って頭悪いよね？ Part13
・底辺私立医大を卒業した医者って頭悪いよね？ Part25
・底辺私立医大を卒業した医者って頭悪いよね？ Part28
・底辺私立医大を卒業した医者って頭悪いよね？ Part8
・底辺私立医大を卒業した医者って頭悪いよね？ Part3
・底辺私立医大を卒業した医者って頭悪いよね？ Part19
・底辺私立医大を卒業した医者って頭悪いよね？ Part5
・底辺私立医大を卒業した医者って頭悪いよね？ Part24
・底辺私立医大を卒業した医者って頭悪いよね？ Part14
・底辺私立医大を卒業した医者って頭悪いよね？ Part30
・底辺私立医大を卒業した医者って頭悪いよね？ Part29
・底辺私立医大を卒業した医者って頭悪いよね？ Part7
・底辺私立医大を卒業した医者って頭悪いよね？ Part27
・底辺私立医大を卒業した医者って頭悪いよね？ Part18
・底辺私立医大を卒業した医者って頭悪いよね？ Part4
・底辺私立医大を卒業した医者って頭悪いよね？ Part26
・底辺私立医大を卒業した医者って頭悪いよね？ Part2
・底辺私立医大を卒業した医者って頭悪いよね？ Part22
・底辺私立医大を卒業した医者って頭悪いよね？ Part20
・底辺私立医大を卒業した医者って頭悪いよね？ Part32
・底辺私立医大を卒業した医者って頭悪いよね？ Part33
・底辺私立医大を卒業した医者って頭悪いよね？ Part15
・底辺私立医大を卒業した医者って頭悪いよね？ Part31
・底辺私立医大を卒業した医者って頭悪いよね？ Part10
・底辺私立医大を卒業した医者って頭悪いよね？ Part11
・底辺私立医大を卒業した頭悪いよね？
・初級英語も和訳できない底辺私立医大卒のスレ
・底辺私立医大卒が国立大学医学部卒を妬むスレ
・宮廷卒なのに、底辺私立医大で学位取得
・日大法現役VS.底辺私立医学部3浪VS.東京大学理三5浪←誰に転生したい？
・底辺国立医学部＝東京大学理科1類、底辺私立医学部＝早慶理工ってマジなんか？
・【底辺私立医学生】順天堂大学裸まつり【良家子息】
・医大卒業して形成外科で研修医やった人って
・原作者って頭悪いよね（確信）
・私立医大はオウム真理教とどう違うんだ？
・不倫って頭悪いよね。あたしでーすｗｗｗ [無断転載禁止]
・私立医大の雄
・【河野防衛相】「感染症にも立ち向かえ」 防衛医大卒業式で大臣訓示
・【防衛医大卒業式】河野太郎防衛相「感染症への対処能力向上を」
・【死亡退院】【未成年へのセクハラ】筑波東病院 横山治之品川区大井慈恵医大卒業
・未だに「洋画に比べて邦画はクソ！」とか言ってる奴って頭悪いよな 超大作SFならともかく人間ドラマやホラーでそんな差あるわけなくね？
・生駒ちゃんねるって生駒が卒業したら生駒だけを取り上げますよね？
・白橋が卒業した後に取り残される松村と衛藤の存在って面白いよね [無断転載禁止]
・俺「あっ、一応世間的には難関大学で知られている有名な私立大学を卒業しました」←どんなイメージ？ [無断転載禁止]
・学者｢生命に必要なリンが不足してるから宇宙人はいない｣（ヽ´ん`）｢リンを必要としない生命の可能性を考えない学者って頭悪いな
・お前らって頭悪いのによくパチンコや麻雀のなんやかんや覚えられるよね
・高校卒業したら宮脇咲良たんは大ブレイクしてや主演映画やゴールデンドラマをバンバンやると思っていたけど全く売れないよね(´・ω・`)
・看板出しただけで宣伝した気になっちゃってるアップフロントって頭悪いの？
・国民的アイドルももクロが紅白卒業宣言したのって去年だけでしょ？今年はしてないよね？
・パチンコ屋って頭悪いよな
・まいやん卒業したら乃木坂終わりだよね？
・ドラクエに変革求めてる人って言っちゃなんだけど頭悪いよね
・生駒ちゃん卒業したら乃木坂終わりだよね？
・振り返ると欅坂って長濱ねるちゃんが卒業したあたりから噛み合わなくなったよね
・愛理が卒業したらハロのエースは室田だよね？ [無断転載禁止]
03:14:56 up 22 days, 13:39, 0 users, load average: 9.43, 9.12, 9.30
in 0.083966970443726 sec
@0.083966970443726@0b7 on 010317
|
@YouTube
@YouTube
@YouTube
@YouTube
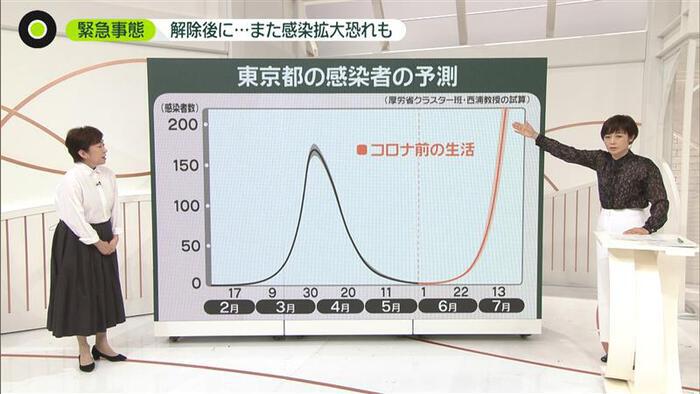
;attredirects=0 
@YouTube
@YouTube
@YouTube
@YouTube
@YouTube
@YouTube
@YouTube
@YouTube
@YouTube
@YouTube
@YouTube
